الگوریتم کراسکال
 | |
| رده | درخت پوشای کمینه |
|---|---|
| ساختمان داده | مجموعههای مجزا (ساختمان داده) |
| کارایی متوسط | |
| پیچیدگی فضایی | |
در نظریه گراف، الگوریتم کراسکال الگوریتمی برای یافتن یک زیرگراف فراگیر همبند با کمترین وزن در یک گراف وزندار است (در یک گراف وزن دار، به هر یال وزنی نسبت داده شدهاست). همچنین این الگوریتم برای یافتن کوچکترین درخت فراگیر در یک گراف وزن دار استفاده میشود.
به عنوان مثال فرض کنید یک شبکه راه آهن که تعدادی شهر را به یکدیگر متصل میکند در دست احداث است میخواهیم با داشتن هزینه مربوط به احداث خط مستقیم بین شهرهای شبکه را طوری طراحی کنیم که مجموع هزینههای ساخت به کمترین مقدار خود برسد. با در نظر گرفتن هر شهر به عنوان یک راس از گراف وزن دار با وزنهای مسئله به یافتن یک زیر گراف فراگیر همبند با کمترین وزن در یک گراف منجر میشود.
فرض کنید وزنها نامنفی هستند بنابراین میتوانیم تصور کنیم که زیر گراف فراگیر با کمترین وزن یک درخت فراگیر از است حال الگوریتم زیر را برای این کار ارائه میدهیم.
الگوریتم کراسکال[ویرایش]
- یال پیوندی را طوری انتخاب کن که وزن آن کوچکترین مقدار موجود باشد.
- اگر یالهای انتخاب شدهاند یال را از میان به گونهای انتخاب کن که:
- زیرگراف با یالهای بدون دور باشد.
- از میان یالهای مشمول شرط (الف) وزن دارای کمترین مقدار ممکن باشد.
- در صورتی که مرحله ۲ دیگر قابل اجرا نیست توقف کن.
برنامهٔ Graph Explorer[ویرایش]
نمونهای از خروجی برنامه:
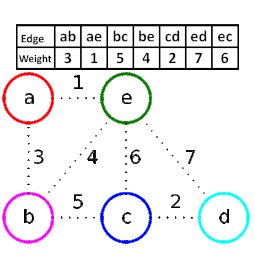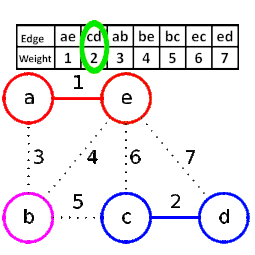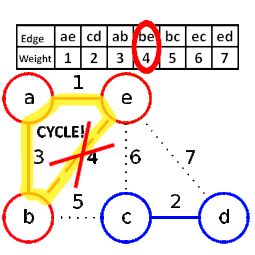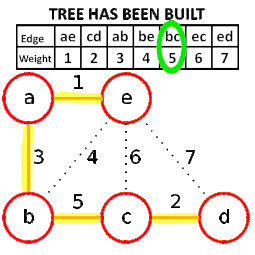
مثال[ویرایش]
اثبات[ویرایش]
ثابت میکنیم هر درخت فراگیر با یالهای که با الگوریتم کراسکال ساخته شود یک درخت بهینهاست.
از طریق تناقض: به ازای هر درخت فراگیر از به غیر از کوچکترین مقدار را به طوری که در نباشد با نمایش میدهیم. اکنون فرض کنید که یک درخت بهینه نباشد و را به عنوان درخت بهینه در نظر بگیرید که در آن دارای بزرگترین مقدار ممکن باشد. فرض کنید این بدان معنی است که هم در و هم در هستند؛ ولی در نیست پس شامل یک دور یکتای میباشد. فرض کنید یالی از باشد که در هست ولی در نیست. پس یال برشی ازT+ نیست؛ بنابراین یک گراف همبند با یال بوده در نتیجه درخت فراگیر دیگری برای خواهد بود. روشن است که:
ولی در الگوریتم کراسکال به عنوان یالی با کمترین وزن طوری انتخاب شدهاست که زیرگراف با یالهای بدون دور باشد. چون زیرگراف با یالهای زیر گرافی از است. بنابرین ان هم بدون دور است و نتیجه میگیریم که:
≥
پس
≤
پس هم یک درخت بهینه خواهد بود در صورتی که داریم:
که این با انتخاب در تناقض است. بنابرین و در نتیجه یک درخت بهینهاست.
شبه کد الگوریتم کراسکال[ویرایش]
مسئله:یک درخت پوشای می نیمم مشخص کنید.
ورودی:عدد صحیح n>=۲، عدد صحیح مثبت m و یک گراف بدون جهت و وزن دار و متصل شامل n گره و m یال. گراف با یک مجموعه E که شامل یالهای گراف همراه با وزنهای آنها است نشان داده میشود
خروجی:مجموعهای از یالها F در یک درخت پوشا مینیمم
* Void kruskal (int n , int m ,
* set _of_edges E,
* set_of_edges & F)
* {
* index i, j;
* Set_pointer p , q ;
* edge e;
* Sort the m edges in E by weight in nondecreasing order ;
* F=∅;
* initial(n); //زیر مجموعه غیر الحاقی n مقدار دهی
* While(number of edges in F is less than n-1){
* e= edge with least weight not yet considered;
* i, j = indices of vertices connected by e ;
* p=find(i);
* q=find(j);
* if(!equal(p,q)){
* merge(p,q);
* add e to F ;
* }
* }
* }
هرگاه n-1 یال در F وجود داشته باشد، از حلقه whileخارج میشویم؛ زیرا در اینصورت، n-1 یال در یک درخت پوشا وجود خواهد داشت
void sort(struct krus ed[],int m)
{
struct krus temp;
for (int i=۰;i<m;i++)
for (int j=i+1;j<m;j++)
if (ed[j].weight<ed[i].weight)
{
temp=ed[i];
ed[i]=ed[j];
ed[j]=temp;
}
}
منابع[ویرایش]
- نظریه گرافها و کاربردهای آن، جی.ای. باندی و یو.اس.ار. مورتی. مترجم حمید ضرابی زاده، مؤسسه فرهنگی دیباگران تهران، ۱۳۷۸
- http://en.wikipedia.org/wiki/Kruskal_algorithm










































