درخت پوشای کمینه
درخت پوشای کمینه یا درخت فراگیر مینیمم در گرافهای ارزش دار (وزن دار) ساخته میشود.
فرض کنید گراف یک گراف همبند باشد (یعنی بین هردو رأس متمایز آن یک مسیر وجود داشته باشد) منظور از یک درخت پوشا از این گراف درختی است که شامل همه رئوس این گراف باشد ولی فقط بعضی از یالهای آن را دربر گیرد. منظور از درخت پوشای مینیمم (برای گراف همبند وزن دار) درختی است که بین درختهای پوشای آن گراف، مجموع وزن یالهای آن، کمترین مقدار ممکن باشد. برای به دست آوردن درخت پوشای بهینه یک گراف جهت دار متصل میتوان از الگوریتمهای متفاوتی استفاده نمود. پنج الگوریتم معروف پیدا کردن درخت پوشای کمینه عبارتند از: الگوریتم کروسکال، الگوریتم پریم، الگوریتم بروکا (سولین)، الگوریتم حذف معکوس و الگوریتم فلوید-وارشال
ویژگیهای درخت پوشای کمینه[ویرایش]
تعداد حالات ممکن:
امکان وجود بیش از یک درخت پوشای کمینه وجود دارد، برای مثال اگر تمام یالها وزن برابری داشته باشند، تمام زیر در ختها درخت پوشای کمینه هستند. اگر وزن هر دو یال با هم متفاوت باشد، تنها یک درخت پوشای کمینه خواهیم داشت.
کم وزنترین یال در برش گراف:
ادعا: اگر گراف را به دو مجموعه V و V′ از راسها افراز کنیم، کموزنترین یال بین یالهایی که یک طرفشان در مجموعه V و طرف دیگرشان در مجموعه V′ است باید جزء درخت پوشای کمینه باشد. (اگر چند یال با کمترین وزن وجود داشت، باید دقیقاً یکی از آنها جزء درخت پوشای کمینه باشد).
کموزنترین یال گراف:
اگر کموزنترین یال گراف یکتا باشد در هر درخت پوشای کمینهای وجود خواهد داشت.
پروزنترین یال هر دور:
اگر یالی در یک دور از تمام یالهای موجود در آن دور وزنش بیشتر باشد، نمیتواند در درخت پوشای کمینه قرار بگیرد. فرض خلف: فرض کنید این یال در یک درخت پوشای کمینه وجود دارد، اگر آن را حذف کنیم درخت به دو مؤلف تقسیم میشود و دور مذکور در گراف اصلی بدون این یال یک مسیر بین این دو مؤلفه میشود. یالی از این مسیر که این مسیر را از این مؤلفه به آن مؤلفه منتقل میکند جایگزین یال حذف شده به درخت اضافه کنید (ممکن است چند یال این کار را بکنند که مهم نیست کدام را انتخاب میکنیم). این یال کموزن تر است پس مجموع وزنهای یالهای درخت جدید کمتر است که با کمینه بودن درخت اول در تناقض است.
کاربرد درخت پوشای کمینه[ویرایش]
در مسائلی که هدف ایجاد شبکهای است که برای ایجاد ارتباط بین هر دو عضو آن هزینهای باید بپردازیم و میخواهیم در نهایت در این شبکه بین هر دو عضو ارتباط وجود داشته باشد، درخت پوشای کمینه همان کم هزینهترین شبکه است. برای مثال فرض کنید در کشوری میخواهیم طوری جادهسازی کنیم که بتوان از هر شهری به هر شهر دیگری سفر کرد و هزینه ساخت جاده بین هر دو شهر را داریم (این هزینه میتواند تابعی بر اساس فاصله ۲ شهر، آب و هوای بین دو شهر فاصله آنها از شرکت راهسازی و … باشد). برای پیدا کردن کم هزینهترین راه، باید درخت پوشای کمینه را بیابیم.
الگوریتم کروسکال[ویرایش]
در الگوریتم کراسکال یالهای گراف را به ترتیب صعودی مرتب میکنیم. از اولین (کوچکترین) یال شروع کرده و هر یال را به گراف اضافه میکنیم به شرط اینکه دور در گراف ایجاد نگردد. این روال را آنقدر ادامه میدهیم تا درخت پوشای بهینه تشکیل گردد.
این الگوریتم نیز مشابه الگوریتم پریم برای یافتن درخت پوشای کمینهٔ یک گراف به کارمی رود. دراین الگوریتم ابتدا یالها از کمترین وزن به بیشترین وزن مرتب میگردند سپس یال هابه ترتیب انتخاب شده و اگر یالی ایجاد حلقه کند و کنار گذاشته میشود. عملیات هنگامی خاتمه مییابد که تمام رأس هابه هم وصل شوند یا اینکه تعداد یالهای موجود در F برابر n-1 شود که n تعداد رأسها است؛ که در بعضی کتابها با نام راشال مطرح شدهاست. شکل زیر مراحل کار را برای یک گراف فرضی نشان میدهد. بیشتر زمان در الگوریتم کروسکال مربوط به مرتبسازی یالهاست، پس اگر تعداد یال e باشد زمان این الگوریتم از مرتبه (e lg e) Ѳ خواهد بود.
نکته: اگر e نزدیک به کران پایین باشد یعنی گراف نسبتاً خلوت بوده و یال کمی داشتهاست. الگوریتم کروسکال از مرتبه روبه رو است:
و اگر e نزدیک به کران بالا باشد یعنی گراف نسبتاً پر باشد و یالهای زیادی داشته باشد:
(n2 lg n) Ѳ = (n2.2 lg n) Ѳ = (n2 lg n2) Ѳ = (e lg e) Ѳ
پس اگر گرافی یالهای کمی دارد بهتراست از روش کروسکال واگر یالهای زیادی دارد بهتراست از روش پریم استفاده کنیم.
1 function Kruskal(G)
2 for each vertex v in G do
3 Define an elementary cluster C(v) ← {v}.
4 Initialize a priority queue Q to contain all edges in G, using the weights as keys.
5 Define a tree T ← Ø //T will ultimately contain the edges of the MST
6 // n is total number of vertices
7 while T has fewer than n-1 edges do
8 // edge u,v is the minimum weighted route from/to v
9 (u,v) ← Q.removeMin()
10 // prevent cycles in T. add u,v only if T does not already contain a path between u and v.
11 // Note that the cluster contains more than one vertex only if an edge containing a pair of
12 // the vertices has been added to the tree.
13 Let C(v) be the cluster containing v, and let C(u) be the cluster containing u.
14 if C(v) ≠ C(u) then
15 Add edge (v,u) to T.
16 Merge C(v) and C(u) into one cluster, that is, union C(v) and C(u).
17 return tree T
نحوهٔ کار الگوریتم کراسکال به این صورت است که یک جنگل از درخت هارا به ترتیب با هم ادغام میکند تا به یک درخت واحد برسد. در اینجا نمونهای از چگونگی عملکرد الگوریتم کراسکال آوردهایم:
الگوریتم پریم[ویرایش]
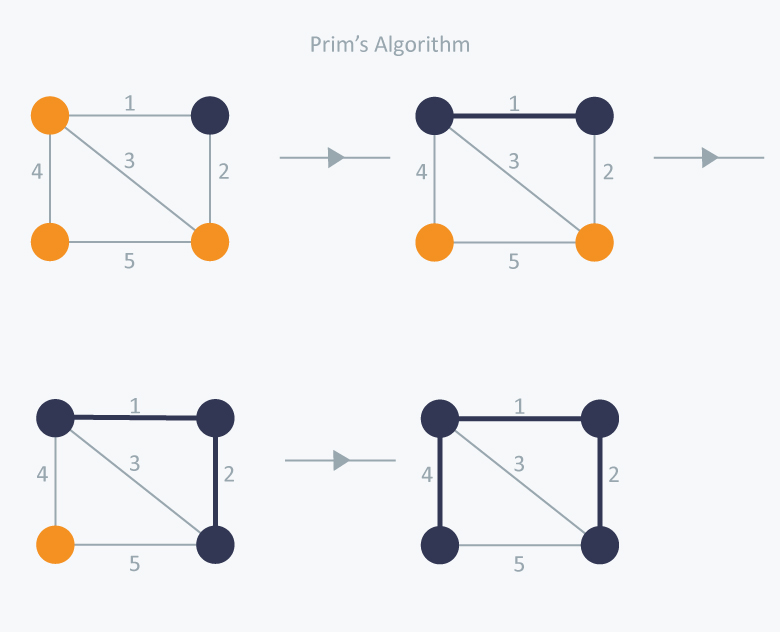
در این روش از یک رأس شروع میکنیم و کمترین یال (یال با کمترین وزن) که از آن میگذرد را انتخاب میکنیم. در مرحله بعد یالی انتخاب میشود که کمترین وزن را در بین یالهایی که از دو گره موجود میگذرد داشته باشیم. به همین ترتیب در مرحله بعد یالی انتخاب میگردد که کمترین وزن را در بین یالهایی که از سه گره موجود میگذرد داشته باشد. این روال را آنقدر تکرار میکنیم تا درخت پوشای بهینه حاصل شود. باید توجه کرد که یال انتخابی در هر مرحله در صورتی انتخاب میشود که در گراف دور ایجاد نکند. تفاوت روش پریم با روش کراسکال در این است که گراف حاصل در مراحل میانی تشکیل درخت پوشای بهینه در روش پریم همیشه متصل است ولی در الگوریتم کراسکال در آخرین مرحله قطعاً متصل است.
while latest_addition = remove minimum in Q
set is_in_Q of latest_addition to false
add latest_addition to (minimum_adjacency_list of (parent of latest_addition))
add (parent of latest_addition) to (minimum_adjacency_list of latest_addition)
for each adjacent of latest_addition
if (is_in_Q of adjacent) and (weight-function(latest_addition, adjacent) <min_distance of adjacent)
set parent of adjacent to latest_addition
set min_distance of adjacent to weight-function(latest_addition, adjacent)
update adjacent in Q, order by min_distance
- ممکن است درختهایی که الگوریتم مذکور تولید میکنند، از لحاظ شکل ظاهری متفاوت باشند، ولی وزن همهٔ درختها یکسان است.
- مرتبهٔ زمانی الگوریتم پریم برابر (o(n^2 است. (حلقهٔ while، برای n دفعه و عمل یافتن از میان لبههای متصل به یک مجموعه دور خاص n دفعه اتفاق میافتد؛ که در مجموع برابر n^2 دفعه میشود).

نمونه مثال الگوریتم پریم
زمان اجرای الگوریتم prim[ویرایش]
به چگونگی پیادهسازی صف اولویت Q بستگی دارد. اگر Q به صورت min-heap دودویی پیادهسازی شود. میتوانیم از روال BUILD-MIN-HEAP در خطوط ۵–۱ برای مقدار دهی اولیه در زمان(O(V استفاده کنیم. بدنه حلقهwhile، |V| بار اجرا میشود؛ و چون هر عمل EXTRACT-MIN زمان(O(lgV را صرف میکند زمان کل برای همه فراخوانی EXTRA-MIN برابر(O(vlogV است. حلقه for در خطوط ۱۱–۸ روی هم رفته (O(E بار اجرا میشود چون مجموعه طول همه لیستهای همجواری برابر ۲|E| میباشد. در داخل حلقه for بررسی برای عضویت در Q در خط ۹ میتواند در زمان ثابت با نگهداری یک بیت برای هر راس که بیان میکند آیا آن راس در Q قرار دارد یا خیر، پیادهسازی میشود و وقتی که راس از Q حذف شود بروز رسانی بیت انجام میگیرید. انتساب در خط۱۱ شامل یک عمل DECREASE- KEY ضمنی بر روی min-heap است که میتواند در min-heap دودویی در زمان(O(lgV پیادهسازی شود؛ بنابراین زمان کل برای الگوریتم Prim برابر(O(VlgV+ ElgV)= O(ElgV است که بهطور مجانبی با پیادهسازی الگوریتم Kruskal یکسان میباشد. اگر heap فیبوناچی برای پیادهسازی صف اولویت مینیمم Q استفاده شود. زمان اجرای الگوریتم Prim به(O(E+VlgV بهبود مییابد.
الگوریتم سولین[ویرایش]
در الگوریتم سولین برای هر گره یال با کمترین هزینه که از آن عبور میکند را رسم میکنیم. در مرحله بعد، گراف به مؤلفههایی تقسیم میشود و یالی انتخاب میگردد که با کمترین هزینه دو مؤلفه گراف را به همدیگر متصل نماید با شرط عدم وجود دور در گراف. آنقدر این مراحل را ادامه میدهیم تا درخت پوشای کمینه حاصل شود.