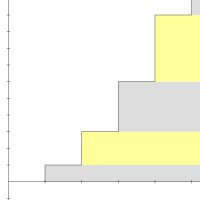
... + ۴ + ۳ + ۲ + ۱

چهار مجموع اول سری . . . +۴+۳+۲+۱

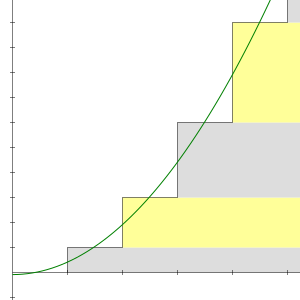
در ریاضیات . . . + ۴ + ۳ + ۲ + ۱ یک سری نامتناهی واگرا از اعداد طبیعی متوالی است که با هم جمع می‌شوند. با استفاده از نمادها و تعریف‌های ریاضی، این سری به این صورت نمایش داده می‌شود:

$\sum _{n=1}^{\infty }n$

همگرایی سری $\sum _{n}^{\infty }a_{n}$ را می‌توان با بررسی کمیت حد $p=\lim _{n\to \infty }a_{n}$ و استفاده از مقایسه‌های زیر تعیین کرد:

اگر 0$\mid p\mid >$ باشد، آنگاه سری واگرا است. به‌طور کلی اگر تابع مربوطه مثبت، ادامه‌دار و در حال افزایش باشد، آنگاه سری واگرا است.

اگر فرض کنیم مجموعه فوق را داریم و آن را S نامیده‌ایم، مجموع عدد ۱ تا n که خود یک تصاعد حسابی با قدر نسبت یک هست، از رابطه فوق به دست می‌آید. $S=1+2+3+4+5+...K$ $\sum _{n=1}^{K}K={\frac {n(n+1)}{2}},$

در ریاضیات اگر حد فرمول بالا را در بینهایت بگیریم، به بینهایت می‌رسیم. $\lim _{N\to \infty }{\frac {n(n+1)}{2}}=\infty$ از آنجا که دنباله یک مجموع جزئی نمی‌تواند به یک سری محدود شود، مجموع ندارد چون کراندار نیست. در ابتدا به نظر می‌رسد که این سری ارزش معناداری ندارد، اما اگر آن را دستکاری کنیم به نتایج جالبی می‌رسیم. در بسیاری از موارد در ریاضیات از روش‌های جمع برای تخصیص عدد حتی به یک سری واگرا استفاده می‌شود.

مثال: مجموعه همگرا C را در نظر بگیریم. $C={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+....$ در ابتدا به نظر می‌رسد که این نیز بینهایت شود، اما با چند عمل ساده یک عدد برای آن به دست آورده می‌شود. در مرحله بعد مجموعه را تقسیم بر دو می‌کنیم.${\frac {1}{2}}C={\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+....$ . اگر آن‌ها را از هم کم کنیم، به یک رابطه ساده می‌رسیم. ${\frac {1}{2}}C={\frac {1}{2}}\Longrightarrow C=1$ .

با استفاده از چند روش می‌توان به رابطه معروف زیر رسید که با یک فرمول بیان می‌شود.

$1+2+3+4+\cdots =-{\frac {1}{12}},$

در این سری، مجموعه ذکر شده نباید به عنوان یک سری بی‌نهایت تفسیر شود، چون چیزی که ما داریم واحد در نظر می‌گیریم دو تا چیز کاملاً بی ربط به یکدیگرند و اساساً از نظر ریاضی نوعی مغلطه و غلط است. اما این روش در برخی مباحث مانند: تئوری کوانتوم و آنالیز مختلط و نظریهٔ ریسمان کاربرد دارد. علت مشهور بودن این رابطه این است که نشان می‌دهد میان ریاضی و فیزیک در مواردی تناقض وجود دارد.

مجموع جزئی

شش جمله اول دنباله مثلثی

مجموع جزئی سری … +۴+۳+۲+۱، سری ۱٬۳,۶٬۱۰٬۱۵ هستند که یک دنباله درجه دو با آهنگ تغییر ۲ می‌باشد. مجموع دنباله تا جمله nام از رابطه زیر به دست می‌آید. $\sum _{k=1}^{n}k={\frac {n(n+1)}{2}}.$ این معادله توسط فیثاغورثیان در قرن ششم پیش از میلاد شناخته شد. چنین اعدادی مثلثی هستند. چون می‌توان آنها را مانند یک مثلث متساوی الاضلاع روی هم چید. دنباله مثلثی به$+\infty$ واگرا می‌شود، پس با این حال دنباله . . . +۴+۳+۲+۱ به بینهایت واگرا می‌شود. اما واگرایی یک نتیجه ساده است که شکل استنباط می‌شود. حد جملات صفر نیست، پس با استفاده از آزمون جمله، سری واگراست.

جمع‌بندی

در میان سری‌های واگرای کلاسیک، دستکاری . . . +۴+۳+۲+۱ در یک محدوده دشوار است. درست است که در ریاضیات از روش‌های جمع بسیاری برای تخصیص عدد به سری واگرا استفاده می‌شود، اما بعضی قوی تر از دیگری هستند. نمونه جالب آن جمع سزارو است که برای استفاده از سری واگرای گراندی استفاده می‌شود. سری گراندی به صورت روبه رو است:$\sum _{n=0}^{\infty }(-1)^{n}=1-1+1-1+...\Longrightarrow {\frac {1}{2}}$

جمع هابل نیز روش قدرتمند دیگری است که نه تنها سری گراندی را با ^۱⁄_۲ جمعبندی می‌کند، حتی سری‌های پیچیده تری مانند $1-2+3-4+...$ را به ^۱⁄_۴ جمعبندی می‌کند که توسط لئونارد اویلر حل شده‌است. برخلاف سری‌های پیشین، سری واگرای $1+2+3+4+...$ ، نه توسط جمع سزار و نه جمع آبل قابل حل است. چون جمع سزار و آبل روی سرهای نوسانی کار می‌کنند و نمی‌توانند یک پاسخ متناهی را به یک سری که به $+\infty$ می‌شود را تولید کنند.بسیاری از تعاریف ابتدایی از مجموع یک سری واگرا، پایدار و خطی هستند، و هر روشی که هم پایدار و هم خطی باشد نمی‌تواند سری $1+2+3+4+...$ را با یک مقدار محدود جمع کند. روش‌های دیگر برای این کار وجود دارد مانند:استفاده از تابع زتا ریمان و جمع رامانوجان. با برخی از روش‌های اکتشافی می‌توان به این نتیجه رسید.

اکتشاف حاصل جمع

یادداشتی از دفتر اول رامانوجان با دست خط خودش که روش حل را نوشته.

رامانوجان، ریاضی‌دان هندی دو روش برای حل مسله استخراج کرد که در فصل۸ اولین دفتر یادداشت خود آن را نوشت. کلید اساسی حل آن این است که سری$1+2+3+4+...$ بسیار نزدیک به سری $1-2+3-4+...$ است. کار با سری نوسانی به مراتب بسیار ساده‌تر است و این نکته حل است. از قرن ۱۸، چندین روش برای مقدار دهی به این سری‌ها مورد بررسی قرار گرفته.

به منظور تبدیل سری $1+2+3+4+...$ به سری $1-2+3-4+...$، می توان از جمله دوم چهار، جمله چهارم هشت و… را کم کرد. برای این کار به ترتیب، مجموعه $C=1+2+3+4+...$ را در نظر می‌گیریم، ($I$)سپس چهار برابر می‌کنیم. ($II$) و از یکیدیگر کم می‌کنیم. ($III$)

${\begin{alignedat}{7}(I)c={}&&1+2&&{}+3+4&&{}+5+6+\cdots \\(II)4c={}&&4&&{}+8&&{}+12+\cdots \\(III)c-4c={}&&1-2&&{}+3-4&&{}+5-6+\cdots \end{alignedat}}$

قسمت دوم اعداد را با فاصله می‌چینیم که در ضمن کم کردن، بتوان یک سری نوسانی به دست آورد. از نظر ریاضی در اینجا نوعی مغالطه رخ می‌دهد. چون در یک مجموعه نامتناهی، حق نداریم جای اعداد به هر شکلی جابجا کنیم.

در اینجا وارد بسط تیلور می‌شویم. تابع 1/²(1 + x) را در نظر می‌گیریم و بسط می‌دهیم. با الگوی زیر مواجه می‌شویم:

${\frac {1}{(1+X)^{2}}}=1-2x+3x^{2}-4x^{3}+5x^{4}-...$

اگر به جای $x$،۱ بگذاریم همان سری مورد نظر تولید می‌شود.

${\frac {1}{(1+1)^{2}}}=1-2+3-4+5-...$

در این حالت با برابر قرار دادن آنها خواهیم داشت:

${\frac {1}{(1+1)^{2}}}=-3c\Longrightarrow -3c={\frac {1}{4}}\Longrightarrow C={\frac {-1}{12}}$

در حالت کلی، دستکاری یک مجموعه نامتناهی به گونه ای که یک متناهی به دست آید، نادرست است. برای مثال اگر اعداد رو به صورت دلخواه جابجا کنیم به نتایجی مانند: ۱=۲ دست می‌یابیم که سازگار نیستند. یا مثلاً اگر صفرها در موقعیت دلخواه درج شوند، در مرحله$4c=0+4+0+8+...$ با قانون جمع همانی قابل توجیه نیست. چون با افزودن یک صفر به جلوی سری به نتایج متفاوتی دست پیدا می‌کنیم. برای درست کردن آن، و محدود کردن صفرها، باید هر عبارت در سری پیگیری شود و به توابع، وابستگی پیوست شود.

تعمیم تابع زتا ریمان

Plot of ζ(s). For s > 1, the series converges and ζ(s) > 1. Analytic continuation around the pole at s = 1 leads to a region of negative values, including ζ(−۱) = −+۱/۱۲.

در منظم سازی تابع زتا، سری ${\textstyle \sum _{n=1}^{\infty }n}$ با سری ${\textstyle \sum _{n=1}^{\infty }n^{-s}}$ جایگزین شده‌است. سری پیش نمونه ای از سری دیریکلت است. در تابع زتا ریمان، اگرsبزرگ‌تر از۱ باشد، سری دیریکلت همگرا می‌شود. مثلا:اگر به جای s،۱ بگذاریم، به صورت روبه رو است:

$$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{1}}}={\frac {1}{1^{1}}}+{\frac {1}{2^{1}}}+{\frac {1}{3^{1}}}+\cdots$$

سری دیریکلت زمانی واگرا می‌شود که s کوچکتر یا مساوی منفی یک باشد؛ بنابراین سری . . . . . زمانی حاصل می‌شود که $s=-1$ باشد. مزیت مهم معرفی تابع زتا ریمان این است که می‌توان آن را برای مقادیر دیگر s، با ادامه تحلیلی تعریف کرد. در اینصورت می‌توان سری $1+2+3+4+...$ با زتای منفی یک($\zeta (-1)$ تعریف کرد. اما طبق تعریف کلاسیک زتا،s باید بزرگ‌تر از یک باشد؛ یعنی تابع زتا را برای هر s نمی‌توان نوشت. این تابع به تابع زتای اویلر معروف است که بعدها با روش ادمه تحلیلی به زتا ریمان رسانده شد. چندین راه برای اثبات $\zeta (-1)={\frac {-1}{12}}$ وجود دارد که با معادله قبلی اشتراکاتی نیز دارد. استفاده از زتا کمی راه حل را کوتاه‌تر می‌کند. یک روش، در امتداد خطوط استدلال اویلر، استفاده از رابطه میان تابع زتای ریمان و تابع دیریکلت استη(s). تابعη(s) با یک سری دیریکله متناوب تعریف می‌شود؛ بنابراین هم تراز با یافته‌های قبلی، دو سری به هم نزدیک و در نهایت برابر می‌شوند به صورت زیر تعریف می‌شوند:

${\begin{alignedat}{7}\zeta (s)&{}={}&1^{-s}+2^{-s}&&{}+3^{-s}+4^{-s}&&{}+5^{-s}+6^{-s}+\cdots &\\2\times 2^{-s}\zeta (s)&{}={}&2\times 2^{-s}&&{}+2\times 4^{-s}&&{}+2\times 6^{-s}+\cdots &\\\left(1-2^{1-s}\right)\zeta (s)&{}={}&1^{-s}-2^{-s}&&{}+3^{-s}-4^{-s}&&{}+5^{-s}-6^{-s}+\cdots &=\eta (s).\end{alignedat}}$

حال محاسبه η(-۱) کار ساده ای است، زیرا تابع دیریکلت برابر با سری هابل است که تعریف کننده آن است.با حد یک طرفه، در همسایگی چپ آن داریم:

$-3\zeta (-1)=\eta (-1)=\lim _{x\to 1^{-}}\left(1-2x+3x^{2}-4x^{3}+\cdots \right)=\lim _{x\to 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.$

با تقسیم بر -۳ به دست می‌آید:

$\zeta (-1)={\frac {-1}{12}}$

منظم سازی تابع قطع

سری 1 + 2 + 3 + 4 + ⋯

بعد از ساده‌سازی (هموار سازی)

روش منظم سازی با استفاده از تابع برش می‌تواند مجموعه را برای رسیدن به${\frac {-1}{12}}$ ساده کند. ساده‌سازی، یک پل مفهومی بین منظم سازی تابع زتا، آنالیز مختلط، جمع رامانوجان با میانبر به فرمول اویلر-مک لارین است. به جای آن، این روش مستقیماً بر روی تبدیل محافظه کارانه سری عمل می‌کند و از آنالیز حقیقی استفاده می‌کند. ایده اصلی این است که سری گسسته غیر نوسانی بدرفتار $\textstyle \sum _{n=0}^{N}n$، با سری هموار و ساده شده جایگزین شود.

$\sum _{n=0}^{\infty }nf\left({\frac {n}{N}}\right),$در این سری تابع f یک تابع قطع با ویژگی خاص است. تابع قطع باید به حالت $f(0)=1$ نرمال شود. این نرمال سازی، چیزی متفاوت تر از آنی است که در معادلات دیفرانسیل استفاده می‌شود. تابع برش باید مشتقات محدود کافی برای صاف کردن موج‌های سری داشته باشد. و باید سریعاً به صفر میل کند. برای راحتی، ممکن است که نیاز باشد تابع f هموار، محدود و تکیه گاه باشد. سپس می‌توان ثابت کرد که مجموع این سری هموار شده، مجانب${\frac {-1}{12}}+CN^{2}$ می‌باشد که C در آن یک عدد ثابت است که به f بستگی دارد. ولی انبساط مجانبی به f بستگی ندارد، بلکه همان مقداری است که توسط ادامه تحلیلی، ${\frac {-1}{12}}$ به دست آمده.

جمع‌بندی رامانوجان

جمع رامانوجان برای سری . . . +۴+۳+۲+۱، همان${\frac {-1}{12}}$ است. رامانوجان در نامه دومش به گادفری هارولد هاردی نوشت:"

آقای محترم. من از مطالعه نامه شما که در۸ فوریه۱۹۱۳ برایم فرستادید بسیار خوشحالم. من انتظار داشتم جوابی مشابه جوابی که یک استاد ریاضیات در لندن نوشت و از من خواست که سری بی‌نهایت برومویچ را با دقت مطالعه کنم و در دام سری‌های واگرا نیفتم بدهید. به او گفتم که مجموع بی‌نهایت، مقررات سری‌های واگرا است. بر اساس نظریه من،$1+2+3+4++...={\frac {-1}{12}}$می‌شود. اگر این را بگویم فوراً تیمارستان را به من نشان خواهید داد. من در این توضیح می‌دهم تا شما را متقاعد کنم که نمی‌توانید از روش‌های اثبات من پیروی کنید، اگر خطوطی را که روی آن‌ها حرکت می‌کنم را در یک نامه مشخص کنم.

جمع رامانوجان روشی برای جداکردن جمله ثابت در فرمول اویلر-مک لارین است که برای پیدا کردن یک مجموع جزئی برای یک سری کاربرد دارد. برای تابع$f$، مجموع کلاسیک

سری$\textstyle \sum _{k=1}^{\infty }f(k)$ رامانوجان، به صورت زیر تعریف می‌شود.

$c=-{\frac {1}{2}}f(0)-\sum _{k=1}^{\infty }{\frac {B_{2k}}{(2k)!}}f^{(2k-1)}(0),$

که f^(2k−1)، مشتق(2k-۱)امین تابع f، و B_2k،

(2k)امین مقدار عدد برنولی است کهB₂ = 1/6 و B₄ = −+۱/۳۰ و… است. با تنظیم کردن f(x) = x، اولین مشتق $f$،۱ می‌شود و تمامی جملات دیگراز بین می‌روند؛ بنابراین جواب به دست می‌آید:

$c=-{\frac {1}{6}}\times {\frac {1}{2!}}=-{\frac {1}{12}}.$

تئوری جدید رامانوجان ایجاب می‌کند که$f$ باقاعده باشد. این به این معناست که مشتق‌های مرتبه بالای f، سریع دچار فروپاشی می‌شوند و باقی جملات فرمول اویلر-مکلارین به سمت صفر گرایش پیدا می‌کنند. رامانوجان صورت ضمنی این را فرض کرده، و صریحاً بیان نکرد.شرط منظم بودن سری‌ها، از استفاده جمع رامانوجان در سری‌های فاصله دار مانند:$0+2+0+4+...$ جلوگیری می‌کند. چون هیچ تابع منظمی این مقادیر را نمی‌گیرد. در عوض چنین سری‌هایی باید با تابع زتا حل و تشریح شود. به همین دلیل هاردی احتیاط زیادی را هنگام استفاده از جمع رامانوجان برای سری‌های شناخته شده برای یافتن مجموع سری‌های مرتبط توصیه می‌کند.

شکست روش‌های جمع خطی پایدار

روش‌هایی که سری‌های همگرا را به یک مقدار مشخص جمع می‌کنند، نمی توانند سری‌های واگرا را به یک مقدار مشخص جمع بزنند. (پایدار به این معنی است که با اضافه کردن یک عبارت به ابتدای سری، مجموع آن، با مقدار عبارت اضافه شده افزایش می‌یابد)می‌توان به صورت زیر آن را توضیح داد:

اگر$X$ برابر با مقدار زیر باشد

$1+2+3+4+...=X$

سپس به هر دو طرف معادله یک صفر اضافه کنیم

$0+1+2+3+4+...=X+0$

با شرط ثابت خطی بودن، میتوان دو معادله بالا را از هم کم کرد.

$1+1+1+1+1+...=X-X=0$

با اضافه کردن مجدد دو صفر به دو طرف معادله به دست می‌آید:

$0+1+1+1+1+...=0$

و دوباره با کم کردن دو سری بالایی به دست می‌آید:

$1+0+0+0+...=0$

که منجر به یک تناقض منطقی می‌شود. که در نتیجه روش‌های پایدار و خطی روش مناسبی برای حل سری واگرای $1+2+3+4+...$نیست.

فیزیک

نظریهٔ ریسمان

در نظریه ریسمان بوزونیک، نظریه اصلی ریسمان، تلاش می‌شود انرژی ممکن سطوح یک رشته محاسبه شود، به خصوص کم‌ترین سطح انرژی یا حد صفر آن. به صورت عامیانه یعنی هر نوسان رشته را می‌توان به عنوان مجموعه ای از نوسانگرهای هماهنگ کوانتومی مستقل D-2 مشاهده کرد. برای هر موج در جهت عرضی (محورy)یکی. که D در آن بعد فضا-زمان است. اگر بسامد نوسان ω باشد، انرژی در یک نوسان گر که به هماهنگ n-ام کمک می‌کند برابرnħω/۲ می‌باشد؛ بنابراین در استفاده از سری واگرا، جمع تمامی هماهنگ‌ها، برابر −ħω(D − ۲)/۲۴ می‌باشد. در نهایت این واقعیت است، همراه با قضیه گودار-تورن، که منجر به عدم سازگاری نظریه ریسمان بوزونی در ابعادی غیر از ۲۶ می‌شود، یعنی ناسازگاری نظریه ریسمان بوزونی در ۲۵ به بعد فضا و ۲۶ به بعد زمان تمام می‌شود.

اثر کاسیمیر

هندریک کاسیمیر، فیزیکدان هلندی مشاهده‌ای انجام داده‌است که به اثر کاسیمیر مشهور است. در آزمایش کاسیمیر، دو صفحه موازی هادی رو در نظر می‌گیریم که در خلأ اند. از نظر فیزیک کلاسیک (نیوتونی) در اینجا هیچ اتفاقی روی نمی‌دهد، اما مقدار بسیار کمی انرژی وجود که به عنوان حد انرژی صفر شناخته می‌شود؛ یعنی کمترین انرژی ممکن همان است، درست مانند حد انرژی موجود در صفر کلوین(۲۷۳- درجهٔ سانتی گراد) که کمترین دمایی است که انسان توانسته به آن برسد. این انرژی کم می‌تواند در اثر فعالیت دنیای زیراتمی باشد. با حساب کردن متوجه می‌شویم که میزان نیرو و چگالی انرژی در سه بعد متناسب با تابع زتای منفی سه$\zeta (-3)$ است که برابر با${\frac {1}{120}}$ است. از تعمیم سری. . . +۴+۳+۲+۱ یا همان تابع زتای منفی یک$\zeta (-1)$ نیز می‌توان برای محاسبه نیرو در اثر کاسیمیر برای یک میدان اسکالر در یک بعد استفاده کرد.یک تابع قطع نمایی برای صاف کردن سری کافی است، که نشان دهنده این واقعیت است که حالت‌های پرانرژی خودسرانه توسط صفحات رسانا مسدود نمی‌شوند. تنها چیزی که باقی می‌ماند عبارت ثابت ۱/۱۲- است و علامت منفی این نتیجه در نیرو نشان دهنده این واقعیت است که پدیده کاسیمیر عجیب و جالب است.

تاریخچه

اینکه لیوناردو اویلر سری را به 1/12- ختم کرده مشخص نیست. طبق گفتهٔ موریس کلاین، کارهای اویلر برای حل سرهای واگرا متکی بر بسط توابع بود که از آن،... +۴+۳+۲+۱ به بینهایت ختم می‌شد. به گفته ریموند ایوب، این حقیقت که سری زتای واگرا، با سری هابل قابل جمع شدن نیست، اویلر را از استفاده آزادانه از تابع زتا مانند تابع eta منع کرد، به همین دلیل نمی‌توانست تابع را جمع کند و به یک مجموعه جزئی برساند.برخی دیگر نویسندگان این مجموع را به اویلر نسبت داده‌اند و عنوان می‌کنند که اویلر رابطه بین توابع زتا و اتا را به اعداد صحیح منفی با استفاده از ادامه تحلیلی گسترش داده‌است. نوشته‌های چاپ شده اولیه، در نشریه ۱۷۶۰ اویلر که در مقاله ای با نام(De seriebus divergentibus)چاپ شد، به سری واگرای . . . +۴+۳+۲+۱ در کنار سری هندسی (با قدر نسبت ۲) . . . +۸+۴+۲+۱ پرداخته‌است. اویلر اشاره می‌کند که سری‌هایی از این نوع می‌توانند به صورت یک مجموعه متناهی و منفی دربیایند، همچنین وی توضیح می‌دهد که برای سری‌های هندسی به چه معناست، اما او توضیحی درباره سری . . . +۴+۳+۲+۱ نداد. در همان مقاله نشریه عنوان کرد جمع سری هندسی … +۱+۱+۱+۱ برابر بینهایت است.

در رسانه

در رمان کارمند هندی، نوشته دیوید لیویت، صحنه‌ای وجود دارد که جان لیتل‌وود و هاردی در مورد مفهوم این سری صحبت می‌کنند. آنها به این نتیجه رسیدند که رامانوجان ζ(-۱) را دوباره کشف کرده‌است، و در نامه دوم خود خط «دیوانه نشین» را به عنوان نشانه ای از اینکه رامانوجان با آنها بازی می‌کند در نظر می‌گیرند. سایمن مک برنی در نمایشنامه عدد در حال ناپدید شدن در سال ۲۰۰۷، در ابتدای سکانس به تمرکز روی این سری می‌پردازد. شخصیت اول فیلم، روث، وارد سالن سخنرانی می‌شود و ایده یک سری واگرا را مطرح می‌کند و قبل از اینکه اسم آن را اعلام کند می‌گوید:می‌خواهم یک چیز جالب به شما نشان دهم، یعنی ^۱⁄_۱۲-= . . . + ۴ + ۳ + ۲ + ۱. همان‌طور که روث مشغول گرفتن مشتق از معادله تابع زتا بود، یکی از بازیگران رو به تماشاچیان می‌کند و اقرار می‌کند که آنها بازیگر هستند ولی ریاضیات واقعی است. ترسناک است اما بازهم واقعی است.در ژانویه ۲۰۱۴، نامبرفیل، یک یوتیوبر، ویدیویی در مورد سری‌ها ساخت که در ماه اول بیش از یک و نیم میلیون بازدید خورد.این ویدیوی هشت دقیقه‌ای توسط تونی پادیلا، استاد فیزیک دانشگاه ناتینگهام، گفته شد. پادیلا با سری . . . +۱+۱–۱+۱–۱+۱–۱ و . . . +۴–۳+۲–۱ شروع کرد و آن دو را با استفاده از تفریق جمله به جمله به سری . . . +۴+۳+۲+۱ رساند.همچنین نامبرفیل یک ویدیوی ۲۱ دقیقه‌ای دیگر را نیز با حضور ادموند کوپلند، فیزیکدان دانشگاه ناتینگهام که توضیحات بیشتری در مورد چگونگی جواب سری^۱⁄_۴=. . . +۴–۳+۲–۱ با استفاده از جمع هابل، و جواب سری ^۱⁄_۱۲-= . . . + ۴ + ۳ + ۲ + ۱ با استفاده از تعمیم تابع زتا منفی یک داده بود، ضبط کرد. پس از انتقاد تماشاگران ویدیو از پادیلا بابت عدم دقت، او یادداشتی در وبلاگ خودش نوشت تا رابطه میان سری دیریکله را ادامه تحلیلی که در ویدیو توضیح داده بود، واضح تر بیان کند.

روزنامه نیویورک تایمز ویدیوی نامبرفیل را پوشش رسانه ای داد. ادوارد فرنکل، ریاضی‌دان، در یادداشتی برای این ویدیو نوشت:

این حساب و کتاب ریاضیاتی یکی از بهترین اسرار ریاضی بود، هیچ‌کس در مورد آن نمی‌دانست

پوشش این موضوع در مجلهٔ اسمیتسونیان، ویدیوی نامبرفیل را مغلطه وار و گمراه کننده توصیف می‌کند و اشاره می‌کند تفسیر جمع این سری مساوی ^۱⁄_۱۲- و براساس تعریف متفاوتی از علامت برابری درست شده‌است. در این تعریف متفاوت از علامت برابری که در ادامه تحلیلی استفاده می‌شود، این علامت به معنای برابری نیست بلکه به معنای «مرتبط با یکدیگر» است. ویدیوی نامبرفیل توسط ریاضیدان آلمانی، بورکارد پلاستر، به همان شیوه مورد نقد قرار گرفت و تا سال ۲۰۲۳، حدود۲٫۷ میلیون بازدید گرفت.

همچنین فیلمی به اسم مردی که بینهایت را می‌دانست از داستان زندگی رامانوجان ساخته شده است.