ماده گران‌رومومسان

گران‌رومومسانی یا ویسکوپلاستیسیته یک نظریه در مکانیک پیوسته است که رفتار وابسته به مقدار، و غیرالاستیک جامدات را، توصیف می‌کند. وابستگی به مقدار در اینجا به این معنی است که تغییر شکل ماده به سرعت اعمال بار بستگی دارد.^[۱] رفتار غیرکشسانی که موضوع ویسکوپلاستیسیته است، مومسانی است که خود به این معنی است که وقتی مقدار بار به میزان خاصی برسد، تغییر شکل مواد غیرقابل برگشت می‌شود. تغییر شکل پلاستیکی وابسته به مقدار برای انجام محاسبات پلاستیسیته گُذر مهم است. تفاوت اصلی بین مدل‌های پلاستیک و ویسکوپلاستیکِ مستقل از مقدار، این است که مدل اخیر نه تنها دچار تغییر شکل دائمی پس از اعمال بار می‌شود، بلکه همچنان تحت تأثیر بارِ اعمال شده، دچار یک جریان خزشی که تابعی از زمان است، می‌شود.

پاسخ الاستیک یک بُعدی مواد ویسکوپلاستیک را می‌توان با عناصر فنری هوک بیان کرد. وابستگی به مقدار را می‌توان به روشی مشابه ویسکوالاستیسیته، با عناصر داشپات غیرخطی نشان داد. پلاستیسیته را می‌توان با افزودن عناصر اصطکاکی لغزشی وارد محاسبه کرد که در شکل ۱ نشان داده شده‌است.^[۲] در این شکل، E مدول الاستیسیته، λ پارامتر ویسکوزیته و N یک پارامتر از نوع قانون قدرتاست که معرف داشپات غیر خطی می‌باشد.

[σ(dε/dt)= σ = λ(dε/dt) ^{(1/N). )}].

عنصر لغزنده می‌تواند دارای تنش تسلیم (σ _y) باشد که به مقدار کُرنش وابسته است، یا حتی ثابت باشد، به گونه ای که در شکل 1c نشان داده شده‌است.

ویسکوپلاستیسیته معمولاً به صورت سه بعدی با استفاده از مدل‌های فرااسترس Perzyna یا Duvaut-Lions مدل‌سازی می‌شود.^[۳] در این مدل‌ها، امکان داده می‌شود که پس از اِعمال بار، تنش تا فراسوی سطح لهیدگی مستقل از مقدار افزایش یابد و سپس در طول زمان آرام به سطح لهیدگی بازگردد. معمولاً در چنین مدل‌هایی فرض می‌شود سطح لهیدگی به مقدار وابسته نیست. یک روش جایگزین، افزودن یک مقدارِ وابستگی به کرنش، به تنش لهیدگی، و استفاده از تکنیک‌های پلاستیسیته مستقل از مقدار برای محاسبه پاسخ یک ماده است.^[۴]

برای فلزات و آلیاژها، ویسکوپلاستیسیته رفتار ماکروسکوپی ناشی از مکانیسمی است که به حرکت نابجایی‌ها در دانه‌ها مرتبط است و اثرات لغزش بین کریستال‌ها هم به آن افزوده می‌گردد. این مکانیسم معمولاً در دماهای بیشتر از تقریباً یک سوم دمای ذوب مطلق، غلبه می‌کند. با این حال، آلیاژهای خاصی در دمای اتاق (300K) خواص ویسکوپلاستیسیته از خود نشان می‌دهند. برای پلیمرها، چوب و قیر، نظریه ویسکوپلاستیسیته باید رفتاری فراتر از حد الاستیسیته یا ویسکوالاستیسیته را توصیف کند.

به‌طور کلی نظریه‌های ویسکوپلاستیسیته در موارد زیر مفید هستند:

محاسبه تغییر شکل‌های دائمی
پیش‌بینی فروپاشی سازه‌های پلاستیکی
بررسی پایداری
شبیه‌سازی خردشدگی
سیستم‌هایی که در معرض دماهای بالا هستند مانند توربین در موتورها. به عنوان مثال، در نیروگاه‌ها.
مشکلات دینامیکی و سیستم‌هایی که در معرض کرنش بالا هستند.

تاریخچه

تاریخچه تحقیق در مورد نظریه‌های پلاستیسیته در سال ۱۸۶۴ با کارهای هنری ترسکا،^[۵] سنت و نانت (۱۸۷۰) و لوی (1871)^[۶] در مورد معیار حداکثر رفتار بُرشی آغاز شد.^[۷] یک مدل پلاستیسیته بهبود یافته در سال ۱۹۱۳ توسط فون میزس^[۸] ارائه شد که اکنون به عنوان معیار لهیدگی فون میزز شناخته می‌شود. در مورد ویسکوپلاستیسیته، تهیه یک مدل ریاضی به سال ۱۹۱۰ برمی گردد که خزش اولیه را با قانون آندراد توصیف می‌کند.^[۹] در سال ۱۹۲۹، نورتون^[۱۰] یک مدل داشپات تک بعدی ایجاد کرد که میزان خزش ثانویه را به تنش مرتبط می‌کرد. در سال ۱۹۳۴، اودکویست^[۱۱] قانون نورتون را به موارد چند محوری تعمیم داد.

مفاهیمی مانند هنجاری بودن جریان پلاستیک نسبت به سطح لهیدگی و قوانین جریان یافتن برای پلاستیسیته، توسط پراندتل (1924)^[۱۲] و رویس (۱۹۳۰) معرفی شدند.^[۱۳] در سال ۱۹۳۲، هوهنمسر و پراگر^[۱۴] اولین مدل برای جریان ویسکوپلاستیک آهسته را ارائه کردند. این مدل رابطه ای بین تنش انحرافی و مقدار کرنش برای یک جامد بینگهام تراکم ناپذیر فراهم کرد.^[۱۵] با این حال، این نظریات قبل از سال ۱۹۵۰ کاربرد نداشت تا اینکه در آن سال قضایای حدی کشف شدند.

در سال ۱۹۶۰، اولین سمپوزیوم IUTAM با عنوان خزش در سازه‌ها توسط Hoff^[۱۶] برگزار شد و همراه با کارهای Hoff Rabotnov, Perzyna, Hult و Lemaitre روی قوانین سخت شدن ایزوتروپیک، و کارهای Kratochvil, Malinini و Khadjinsky, Ponter و Leckie، و Chaboche روی قوانین سخت شدن سینماتیک، ویسکوپلاستیسیته، را توسعه داد. در سال 1963 Perzyna یک ضریب ویسکوزیته (گرانروی) را معرفی کرد که به دما و زمان بستگی داشت.^[۱۷] مدل‌های تهیه شده مطابق با ترمودینامیک فرآیندهای برگشت‌ناپذیر و دیدگاه پدیدارشناسی مربوطه بود. ایده‌های ارائه شده در این آثار مبنایی برای اکثر تحقیقات بعدی روی پلاستیسیته وابسته به مقدار بود.

پدیدارشناسی

در راستای تجزیه و تحلیل کِیفی، چند تست مشخصات برای توصیف پدیدارشناسی مواد ویسکوپلاستیک انجام می‌شود. چند نمونه از این تست‌ها عبارتند از:^[۹]

تست سخت شدن تحت مقدار تنش یا کرنش ثابت
تست خزش تحت نیروی ثابت
رهایی (relaxation) تنش تحت افزایش طول ثابت

تست سخت شدگی کرنش

شکل ۲. پاسخ تنش-کرنش یک ماده ویسکوپلاستیک تحت مقادیرکرنش‌های مختلف. خطوط نقطه چین پاسخ را در حالتی که مقدار کرنش ثابت نگاه داشته شود نشان می‌دهد. خط آبی پاسخ را هنگام تغییر ناگهانی مقدار کرنش نشان می‌دهد.

یکی از پیامدهای تسلیم این است که با ادامه تغییر شکل پلاستیکی، برای تولید کرنش اضافی باید تنش را افزایش داد. این پدیده را سخت شدگی کرنش/کار می‌نامند.^[۱۸] برای مواد ویسکوپلاستیک، منحنی سخت شدگی تفاوت قابل توجهی نسبت به منحنی‌های سخت شدگی مواد پلاستیکی مستقل از مقدار ندارد. با این وجود، سه تفاوت اساسی را می‌توان مشاهده کرد.

اگر کرنش یکسان باشد، هر چه میزان کرنش بیشتر باشد، تنش بیشتر است.
تغییر در مقدار کرنش در طول تست منجر به تغییر فوری منحنی تنش-کرنش می‌شود.
مفهوم حدّ لهیدگی پلاستیک دیگر کاملاً قابل اعمال نیست.

هر گاه کرنش کم باشد، فرضیه قسمت بندی کرنش‌ها با جداسازی قطعات الاستیک و پلاستیک همچنان قابل اعمال است، یعنی:

{\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}_{\mathrm {e} }+{\boldsymbol {\varepsilon }}_{\mathrm {vp} }

در اینجا، ${\boldsymbol {\varepsilon }}_{\mathrm {e} }$ کرنش الاستیک است و ${\boldsymbol {\varepsilon }}_{\mathrm {vp} }$ معادل کرنش ویسکوپلاستیک است.

برای به دست آوردن رفتار تنش-کرنش نشان داده شده به رنگ آبی در شکل، ماده در ابتدا با مقدار کرنش 0.1/s بارگذاری می‌شود. سپس مقدار کرنش فوراً به 100/s افزایش می‌یابد و برای مدتی در آن مقدار ثابت می‌ماند. در پایان این دوره زمانی، نرخ کرنش بلافاصله به 0.1/s کاهش می‌یابد و این چرخه با افزایش مقادیر کرنش ادامه می‌یابد. به وضوح بین تغییر مقدار کرنش و پاسخ به تنش تأخیر وجود دارد. این تأخیر به‌طور کاملاً دقیق توسط مدل‌های فراتنش مدل‌سازی شده‌است (مانند مدل Perzyna) اما نه توسط مدل‌های پلاستیسیته مستقل از مقدار که دارای تنش لهیدگی وابسته به مقدار هستند.

تست خزش

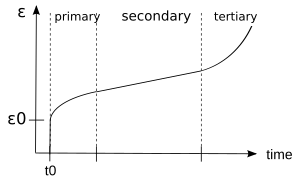خزش، تمایل یک ماده جامد به حرکت آهسته یا تغییر شکل دائمی تحت تنش ثابت است. تست خزش پاسخ کرنشی را به تنش ثابت (همان‌طور که در شکل ۳ نشان داده شده) اندازه‌گیری می‌کند. منحنی خزش کلاسیک نشان دهنده تکامل کرنش به عنوان تابعی از زمان در ماده ای است که تحت تنش تک محوری در دمای ثابت می‌باشد. برای مثال، تست خزش توسط اعمال نیرو / تنش ثابت و تحلیل پاسخ کرنشی سیستم انجام می‌شود. به‌طور کلی (همان‌طور که در شکل b 3 نشان داده شده) این منحنی معمولاً سه فاز یا دوره رفتار را نشان می‌دهد.^[۹]

مرحله خزش اولیه، که همچنین به عنوان خزش گُذر شناخته می‌شود، شامل مرحله شروع خزش است که طی آن، سخت شدن مواد منجر به کاهش مقدار جریان یافتن می‌شود که در ابتدا بسیار بالا است. $(0\leq {\boldsymbol {\varepsilon }}\leq {\boldsymbol {\varepsilon }}_{1})$ .
مرحله خزش ثانویه، که همچنین به عنوان حالت پایدار شناخته می‌شود، موقعی است که مقدار کرنش ثابت است. $({\boldsymbol {\varepsilon }}_{1}\leq {\boldsymbol {\varepsilon }}\leq {\boldsymbol {\varepsilon }}_{2})$ .
مرحله خزش سوم، که در آن افزایش مقدار کرنش تا میزان کرنش گسیختگی روی می‌دهد. $({\boldsymbol {\varepsilon }}_{2}\leq {\boldsymbol {\varepsilon }}\leq {\boldsymbol {\varepsilon }}_{R})$ .

تست رهایی

همان‌طور که در شکل ۴ نشان داده شده، تست رهایی^[۱۹] به عنوان پاسخ تنشیِ ناشی از یک کرنش ثابت در یک دوره زمانی تعریف شده‌است. در مواد ویسکوپلاستیک، تست رهایی، رهایی تنش را تحت بارگذاری تک محوری با وجود یک کرنش ثابت نشان می‌دهد. در واقع، این تست‌ها ویسکوزیته را مشخص می‌کنند و می‌توان از آنها برای تعیین رابطه بین تنش و مقدار کرنش ویسکوپلاستیک استفاده کرد. مقدار کرنش تجزیه عبارت است از:

{\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}}{\mathrm {d} t}}={\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}_{\mathrm {e} }}{\mathrm {d} t}}+{\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}_{\mathrm {vp} }}{\mathrm {d} t}}~.

بخش الاستیک مقدار کرنش توسط معادله زیر بدست می‌آید:

{\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}_{\mathrm {e} }}{\mathrm {d} t}}={\mathsf {E}}^{-1}~{\cfrac {\mathrm {d} {\boldsymbol {\sigma }}}{\mathrm {d} t}}

برای ناحیه صاف منحنی کرنش-زمان و کل مقدار کرنش صفر است. از این رو داریم:

{\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}_{\mathrm {vp} }}{\mathrm {d} t}}=-{\mathsf {E}}^{-1}~{\cfrac {\mathrm {d} {\boldsymbol {\sigma }}}{\mathrm {d} t}}

بنابراین، منحنی رهایی را می‌توان برای تعیین مقدار کرنش ویسکوپلاستیک و درنتیجه، ویسکوزیته داشپات در یک مدل مواد ویسکوپلاستیک یک بُعدی استفاده کرد. وقتی تنش در پایان تست رهایی به حالت یکنواخت می‌رسد، مقدار باقیمانده حاصله، معرف حد بالایی الاستیسیته است. برای برخی مواد مانند سنگ نمک، این حد بالایی الاستیسیته در مقادیر بسیار کم‌تنش روی می‌دهد و تست رهایی را می‌توان بیش از یک سال بدون مشاهده هیچ گونه حالت تنش یکنواخت ادامه داد.

توجه به این نکته ضروری است که انجام تست رهایی بسیار دشوار است زیرا حفظ وضعیت ${\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}}{\mathrm {d} t}}=0$ در تست به ظرافت قابل توجهی نیاز دارد.^[۲۰]

جستارهای وابسته

منابع

↑ Perzyna, P. (1966), "Fundamental problems in viscoplasticity", Advances in Applied Mechanics, 9 (2): 244–368.
↑ J. Lemaitre and J. L. Chaboche (2002) "Mechanics of solid materials" Cambridge University Press.
↑ Simo, J.C.; Hughes, T.J.R. (1998), Computational inelasticity
↑ Batra, R. C.; Kim, C. H. (1990), "Effect of viscoplastic flow rules on the initiation and growth of shear bands at high strain rates", Journal of the Mechanics and Physics of Solids, 38 (6): 859–874, Bibcode:1990JMPSo..38..859B, doi:10.1016/0022-5096(90)90043-4.
↑ Tresca, H. (1864), "Sur l'écoulement des Corps solides soumis à des fortes pressions", Comptes Rendus de l'Académie des Sciences de Paris, 59: 754–756.
↑ Levy, M. (1871), "Extrait du mémoire sur les equations générales des mouvements intérieures des corps solides ductiles au dela des limites ou l'élasticité pourrait les ramener à leur premier état", J Math Pures Appl, 16: 369–372.
↑ Kojic, M. and Bathe, K-J. , (2006), Inelastic Analysis of Solids and Structures, Elsevier.
↑ von Mises, R. (1913) "Mechanik der festen Korper im plastisch deformablen Zustand." Gottinger Nachr, math-phys Kl 1913:582–592.
↑ ^۹٫۰ ^۹٫۱ ^۹٫۲ Betten, J. , 2005, Creep Mechanics: 2nd Ed., Springer.
↑ Norton, F. H. (1929). Creep of steel at high temperatures. McGraw-Hill Book Co. , New York.
↑ Odqvist, F. K. G. (1934) "Creep stresses in a rotating disc." Proc. IV Int. Congress for Applied. Mechanics, Cambridge, p. 228.
↑ Prandtl, L. (1924) Proceedings of the 1st International Congress on Applied Mechanics, Delft.
↑ Reuss, A. (1930), "Berücksichtigung der elastischen Formänderung in der Plastizitätstheorie", Zeitschrift für Angewandte Mathematik und Mechanik, 10 (3): 266–274, Bibcode:1930ZaMM...10..266R, doi:10.1002/zamm.19300100308
↑ Hohenemser, K.; Prager, W. (1932), "Fundamental equations and definitions concerning the mechanics of isotropic continua", Journal of Rheology, 3 (1): 16, Bibcode:1932JRheo...3...16H, doi:10.1122/1.2116434
↑ Bingham, E. C. (1922) Fluidity and plasticity. McGraw-Hill, New York.
↑ Hoff, ed. , 1962, IUTAM Colloquium Creep in Structures; 1st, Stanford, Springer.
↑ Lubliner, J. (1990) Plasticity Theory, Macmillan Publishing Company, NY.
↑ Young, Mindness, Gray, ad Bentur (1998): "The Science and Technology of Civil Engineering Materials," Prentice Hall, NJ.
↑ François, D. , Pineau, A. , Zaoui, A. , (1993), Mechanical Behaviour of Materials Volume II: Viscoplasticity, Damage, Fracture and Contact Mechanics, Kluwer Academic Publishers.
↑ Cristescu, N. and Gioda, G. , (1994), Viscoplastic Behaviour of Geomaterials, International Centre for Mechanical Sciences.

پیوند به بیرون

[Perzyna-1] Perzyna, P. (1966), "Fundamental problems in viscoplasticity", Advances in Applied Mechanics, 9 (2): 244–368.

[2] J. Lemaitre and J. L. Chaboche (2002) "Mechanics of solid materials" Cambridge University Press.

[Simo-3] Simo, J.C.; Hughes, T.J.R. (1998), Computational inelasticity

[Batra-4] Batra, R. C.; Kim, C. H. (1990), "Effect of viscoplastic flow rules on the initiation and growth of shear bands at high strain rates", Journal of the Mechanics and Physics of Solids, 38 (6): 859–874, Bibcode:1990JMPSo..38..859B, doi:10.1016/0022-5096(90)90043-4.

[Tresca-5] Tresca, H. (1864), "Sur l'écoulement des Corps solides soumis à des fortes pressions", Comptes Rendus de l'Académie des Sciences de Paris, 59: 754–756.

[Levy-6] Levy, M. (1871), "Extrait du mémoire sur les equations générales des mouvements intérieures des corps solides ductiles au dela des limites ou l'élasticité pourrait les ramener à leur premier état", J Math Pures Appl, 16: 369–372.

[Kojic-7] Kojic, M. and Bathe, K-J. , (2006), Inelastic Analysis of Solids and Structures, Elsevier.

[Mises-8] von Mises, R. (1913) "Mechanik der festen Korper im plastisch deformablen Zustand." Gottinger Nachr, math-phys Kl 1913:582–592.

[Betten-9] ۹٫۰ ^۹٫۱ ^۹٫۲ Betten, J. , 2005, Creep Mechanics: 2nd Ed., Springer.

[Norton-10] Norton, F. H. (1929). Creep of steel at high temperatures. McGraw-Hill Book Co. , New York.

[Odqvist-11] Odqvist, F. K. G. (1934) "Creep stresses in a rotating disc." Proc. IV Int. Congress for Applied. Mechanics, Cambridge, p. 228.

[Prandtl-12] Prandtl, L. (1924) Proceedings of the 1st International Congress on Applied Mechanics, Delft.

[Reuss-13] Reuss, A. (1930), "Berücksichtigung der elastischen Formänderung in der Plastizitätstheorie", Zeitschrift für Angewandte Mathematik und Mechanik, 10 (3): 266–274, Bibcode:1930ZaMM...10..266R, doi:10.1002/zamm.19300100308

[Hohen-14] Hohenemser, K.; Prager, W. (1932), "Fundamental equations and definitions concerning the mechanics of isotropic continua", Journal of Rheology, 3 (1): 16, Bibcode:1932JRheo...3...16H, doi:10.1122/1.2116434

[Bingham-15] Bingham, E. C. (1922) Fluidity and plasticity. McGraw-Hill, New York.

[Hoff-16] Hoff, ed. , 1962, IUTAM Colloquium Creep in Structures; 1st, Stanford, Springer.

[17] Lubliner, J. (1990) Plasticity Theory, Macmillan Publishing Company, NY.

[18] Young, Mindness, Gray, ad Bentur (1998): "The Science and Technology of Civil Engineering Materials," Prentice Hall, NJ.

[Francois-19] François, D. , Pineau, A. , Zaoui, A. , (1993), Mechanical Behaviour of Materials Volume II: Viscoplasticity, Damage, Fracture and Contact Mechanics, Kluwer Academic Publishers.

[Cristescu-20] Cristescu, N. and Gioda, G. , (1994), Viscoplastic Behaviour of Geomaterials, International Centre for Mechanical Sciences.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]

[۸]

[۹]

[۱۰]

[۱۱]

[۱۲]

[۱۳]

[۱۴]

[۱۵]

[۱۶]

[۱۷]

[۱۸]

[۱۹]

[۲۰]