الگوریتم متروپلیس-هیستینگز
در علم آمار و فیزیک آماری، الگوریتم متروپلیس-هیستینگز (به انگلیسی: Metropolis–Hastings algorithm) یک روش زنجیره مارکوف مونت کارلو (به انگلیسی: Markov chain Monte Carlo) برای به دست آوردن ترتیبی از نمونههای تصادفی از یک توزیع احتمالی است که نمونهبرداری مستقیم از آن دشوار میباشد. این ترتیب را میتوان برای برآورد یک توزیع (به عنوان مثال تولید یک هیستوگرام) یا برای محاسبهٔ برخی انتگرالها (بهطور مثال یک امید ریاضی) استفاده کرد. متروپلیس-هیستینگز و دیگر الگوریتمهای MCMC عموماً برای نمونهبرداری از توزیعهای چند بعدی استفاده میشوند، به خصوص زمانی که تعداد ابعاد بالا باشد. برای توزیعهای تک بعدی معمولاً روشهای دیگری وجود دارند (به عنوان مثال نمونهگیری عدم پذیرش تطبیقی) که میتوانند بهطور مستقیم نمونههای مستقل را از توزیع بازگردانند؛ معمولاً این روشها با مشکل خودهمبستگی که در روشهای MCMC به صورت ذاتی وجود دارند، رو به رو نیستند.[۱]
تاریخچه[ویرایش]
این الگوریتم به افتخار نیکلاس متروپلیس (به انگلیسی: Nicholas Metropolis) که در سال ۱۹۵۳ در مقالهای با عنوان «معادلهٔ محاسبهٔ حالت به وسیلهٔ ماشینهای رایانش سریع» به همراه همکارانش (آریانا روزنبلوث (به انگلیسی: Arianna W. Rosenbluth)، مارشال روزنبلوث (به انگلیسی: Marshall N. Rosenbluth)، اگوستا تلر (به انگلیسی: Augusta H. Teller) و ادوارد تلر (به انگلیسی: Edward Teller) منتشر کردهاست، نامگذاری شده. این مقاله الگوریتمی برای توزیعهای پیشنهادی متقارن ارائه میدهد و سپس هیستینگز در سال ۱۹۷۰ الگوریتم را برای حالتهای عمومیتر توسعه میدهد.[۱][۲]
متروپولیس و اولام در سال ۱۹۴۹ برای تولید نمونه ای از یک تابع چگالی استفاده از الگوریتم متروپولیس را توسط یک تابع چگالی پیشنهادی q متقارن معرفی نمودند. متقارن بودن به این معنی است که به ازای هر x و y داشته باشیم: (q(x,y) = q(y,x. در سال ۱۹۵۳ متروپولیس و همکارانش به مطالعه بیشتر این الگوریتم پرداختند. بعدها در سال ۱۹۷۰ هیستینگز شرط متقارن بودن را حذف نمود و الگوریتم متروپلیس-هیستینگز نامیده شد. انواع دیگر این الگوریتم بر اساس ویژگیهای تابع تولید کنندهٔ نمونه در سالهای بعد معرفی شدند.[۳]
در مورد این که توسعهٔ این الگوریتم دقیقاً به چه کسی نسبت داده شود بحثهایی وجود دارد. متروپلیس عبارت «مونت کارلو» در این زمینه را قبلتر در مقالهای به همراه استانیسلاو اولام استفاده کردهبوده، همچنین با بحثهای محاسباتی این روش آشنا بود و گروهی را در بحثهای نظری مربوط به طراحی و ساخت کامپیوتر مانیاک۱ که برای آزمایشهای این روش در سال ۱۹۵۲ استفاده میشد، رهبری میکرد. هرچند تا قبل از سال ۲۰۰۳ هیچ شرح دقیقی از فرایند توسعهٔ الگوریتم وجود نداشت. در آن زمان مارشال روزنبلات، کمی قبلتر از مرگش، در کنفرانسی در سال ۲۰۰۳ در آزمایشگاه ملی لوسآلموس که برای پاسداشت پنجاهمین سالگرد انتشار مقاله برگزار شدهبود، شرکت کرد و الگوریتم و فرایند توسعهٔ آن را در ارائهای با عنوان «پیدایش الگوریتم مونت کارلو برای مکانیک آماری» شرح داد.[۴] شفافسازیهای تاریخی بعدی به وسیلهٔ گوبرناتیس در مقالهای در سال ۲۰۰۵ انجام شد.[۵] روزنبلات به صورت شفافی بیان میکند که او و همسرش آریانا توسعهٔ الگوریتم را انجام دادهاند و متروپلیس نقشی در توسعهٔ آن به جز فراهم کردن زمان کامپیوتر نداشتهاست.
این مطلب با حرفهای ادوارد تلر که در خاطراتش اذعان میکند پنج نویسندهٔ مقالهٔ سال ۱۹۵۳ با هم برای روزها (و شبها) کار میکردهاند تناقض دارد.[۶] در مقابل، شرح با جزئیات روزنبلات بیان میکند که تلر نقشی اساسی ولی اولیه در پیشنهاد ایدهٔ «بهره بردن از مکانیک آماری و گرفتن مجموعهای از میانگینها به جای استفادهٔ مفصل از سینماتیک» داشتهاست. روزنبلات میگوید این موضوع باعث شد او دربارهٔ عمومی کردن راهکار مونت کارلو بیندیشد؛ موضوعی که وی معمولاً با فون نیومن دربارهٔ آن بحث میکردهاست. آریانا بیان میکند (به گورنتیس در سال ۲۰۰۳) که آگوستا تلر کارهای کامپیوتری را آغاز کرد ولی آریانا آن را ادامه داد و کد مربوطه را از ابتدا نوشت. روزنبلات در یک تاریخ شفاهی که چندی قبل از مرگش ضبط شده[۷] یک بار دیگر نیز تلر را کسی معرفی میکند که مسئلهٔ اولیه را ارائه کرده و خودش را کسی میداند که مسئله را حل کرده و آریانا را برنامهنویس راه حل این مسئله معرفی میکند. از دید اعتبار سخن، دلایل چندانی برای این که اعتبار حرفهای روزنبلات را زیر سؤال ببریم وجود ندارد. در یک شرححال از زندگی روزنبلات فریمن دایسون دربارهٔ او مینویسد:
بارهای زیادی پیش روزنبلات آمدم و از او سؤالی پرسیدم [...] و در طول دو دقیقه پاسخی از او دریافت کردم. سپس برای من معمولاً یک هفته کار میبرد تا جزئیات این که چرا پاسخ روزنبلات درست بودهاست را متوجه شوم. او توانایی خارقالعادهای در دیدن عمق وضعیت یک مسئلهٔ فیزیکی پیچیده و رسیدن به پاسخ درستی به کمک استدلالهای فیزیکی داشت. انریکو فرمی تنها فیزیکدان دیگری بود که من میشناسم که در درک شهودی فیزیک توانایی مشابهی با روزنبلات داشت.[۱][۸]
معرفی[ویرایش]
هنگام انجام استنتاج بیزی، هدف ما محاسبه و استفاده از توزیع مشترک پسین کامل مجموعه ای از متغیرهای تصادفی است. متأسفانه، این روش اغلب نیاز به محاسبهٔ انتگرالی غیرقابل حل دارد. در چنین مواردی ممکن است ما در برابر حل معادلات تحلیلی تسلیم شویم و روش نمونهگیری مبتنی بر روش زنجیره مارکوف مونت کارلو را ادامه دهیم. وقتی از زنجیره مارکوف مونت کارلو استفاده میکنیم با استفاده از نمونهای شبیهسازی شده از توزیع پیشین، توزیع پسین و انتگرالهای غیرقابل حل را تخمین میزنیم.[۹]
معرفی روشهای نمونهبرداری برای تخمین توزیع احتمال[ویرایش]
به صورت کلی روشهای نمونهبرداری (که روشهای مونت کارلو نیز نامیده میشوند) به چهار دسته تقسیم میشوند:
- نمونهبرداری پیشرو (به انگلیسی: forward sampling)
- نمونهبرداری بازپسزننده (به انگلیسی: rejection sampling)
- نمونهبرداری بر پایهٔ اهمیت (به انگلیسی: importance sampling)
- زنجیرهٔ مارکف مونت کارلو (به انگلیسی: Markov chain Monte Carlo)
مشکلات روش نمونهبرداری پیشرو[ویرایش]
یکی از سادهترین روشهای نمونهبرداری در شبکههای بیزی روش نمونهبرداری پیشرو است که با داشتن یک مرتبسازی موضعی از گراف، نمونهبرداری از متغیرها را انجام میدهد. در این روش اگر تعداد متغیرهای شواهد زیاد باشد، بسیاری از نمونهها حذف میشوند و در نتیجه برای تخمین دقیقتر باید از نمونههای بیشتری استفاده شود.
در بسیاری از موارد به دلیل پیچیده بودن توزیع اصلی نمیتوان بهصورت مستقیم از توزیع موردنظر نمونهبرداری کرد، بلکه از توزیع پیشنهادی نمونهبرداری میکنیم. روشهای نمونهبرداری بازپسزننده و نمونهبرداری بر پایهٔ اهمیت از این ایده استفاده میکنند.[۱۰]
مشکلات روش نمونهبرداری بازپسزننده[ویرایش]
در روش نمونهبرداری بازپسزننده اگر توزیع پیشنهادی تفاوت زیادی با داشته باشد؛ اکثر نمونهها پذیرفته نمیشوند. همچنین در این روشها مشکل نفرین ابعاد وجود دارد؛ یعنی با افزایش ابعاد توزیع موردنظر، احتمال پذیرفته نشدن نمونهها به صورت نمایی افزایش مییابد.[۱۰]
مشکلات نمونهبرداری بر پایهٔ اهمیت[ویرایش]
در روش نمونهبرداری بر پایهٔ اهمیت اگر توزیع پیشنهادی تفاوت زیادی با داشته باشد؛ اکثر نمونهها وزن بسیار کمی خواهند داشت و با توجه به وزن آنها رسیدن به نمونههای مناسبی از توزیع دشوار خواهد بود.[۱۱]
معرفی روشهای نمونهبرداری بر اساس زنجیرهٔ مارکف[ویرایش]
یکی از روشهای دیگر نمونهبرداری روش زنجیرهٔ مارکف مونت کارلو است. در این روش از توزیع پیشنهادی استفاده نمیشود، بلکه از توزیع پیشنهادی استفاده میشود که در آن نمونه جدید به دست آمده و آخرین نمونهٔ پذیرفته شدهاست. همزمان با تغییر ، نیز تغییر میکند.
روشهای زنجیرهٔ مارکف مونت کارلو به دو روش نمونهبرداری گیبز و نمونهبرداری متروپلیس-هیستینگز تقسیم میشوند.
محدودیتهای روش نمونهبرداری گیبز[ویرایش]
برای استفاده از روش گیبز باید را محاسبه کنیم. اگرچه این توزیع برای مدلهای گرافی گسسته قابل بدست آوردن است؛ اما برای مدلهای گرافی پیوسته به راحتی قابل محاسبه نیست. محدودیت مهمتری که در این روش وجود دارد این است که زنجیرهٔ گیبز تنها حرکات محدودی در فضای دامنهٔ متغییرهای تصادفی توزیع انجام میدهد. در این روش هر بار تنها یک متغیر تغییر میکند. در مدلهایی که متغییرهای آن به شدت به هم وابسته هستند، چنین تغییری منجر به این خواهد شد که از حالتهایی که احتمال بالایی برای وقوع دارند به حالتهایی منتقل شویم که احتمال بسیار پایینی برای وقوع دارند. در این صورت حالتهای با احتمال بالا بیشتر نمونههای تولید شده را دربر خواهندگرفت و این موضوع باعث میشود زنجیره به سختی بتواند از آن نمونهها فاصله بگیرد که به معنی سرعت پایین همگرایی آن به توزیع اصلی خواهد بود. در این صورت ما معمولاً روشهایی را ترجیح میدهیم که حرکات آنها برد بیشتری داشته باشد و در نتیجه اجازهٔ حرکت بیشتری در فضای دامنهٔ توزیع احتمالی به ما بدهد. الگوریتم متروپلیس-هیستینگز یکی از این راهکارها میباشد.
به صورت کلی محدودیتهای بسیاری برای روشهای بیزی وجود دارد. حتی با داشتن توزیع مشترک پسین، ممکن است استفاده از آن برای به دست آوردن توزیع شرطی برای هر یک از متغییرهای تصادفی موجود در مدل امکانپذیر و عملی نباشد. با داشتن احتمال شرطی پسین همچنان ممکن است آنها از یک فرم شناخته شده نباشند و راه سادهای برای نمونهگیری از آنها وجود نداشته باشد.
نحوهٔ استفاده از زنجیرهٔ مارکف برای نمونهبرداری از یک توزیع احتمالی[ویرایش]
روشهای زنجیرهٔ مارکف مونت کارلو (MCMC) با قدم زدن تصادفی در طول یک زنجیرهٔ مارکف نمونهبرداری از یک توزیع را انجام میدهند. بهعبارت دیگر توزیع اصلی موردنظر را برابر توزیع حالت پایدار یک زنجیرهٔ مارکف در نظر میگیرند و بنابراین اگر بتوان زنجیرهٔ مارکفی طراحی کرد که دارای توزیع حالت پایدار باشد، میتوان با شروع از یک وضعیت اولیهٔ تصادفی در زنجیره مارکف و حرکت مطابق با ماتریس انتقال بین وضعیتها، درنهایت پس از تعدادی حرکت در زنجیرهٔ مارکف به نمونهای از توزیع حالت پایدار و در نتیجه نمونههایی از توزیع اصلی رسید.
شرایط لازم برای استفاده از یک زنجیرهٔ مارکف برای نمونهبرداری[ویرایش]
باید توجه داشت که یک زنجیرهٔ مارکف برای این که مناسب نمونهبرداری باشد، باید هم توزیع حالت پایدار داشتهباشد و هم این توزیع برای آن صرفنظر از وضعیت شروع، یکتا باشد. این موضوع به عنوان یک قضیه در نظریهٔ مدلهای گرافی احتمالی مطرح و اثبات میشود.
شرط این که یک زنجیرهٔ مارکف دارای توزیع حالت پایدار باشد، داشتن خاصیت برگشتپذیری (به انگلیسی: Reversibility) است.
خاصیت برگشتپذیری[ویرایش]
اگر شرط «تعادل جزء به جزء» (به انگلیسی: Detailed Balance) برای یک زنجیرهٔ مارکف برقرار باشد، زنجیره مارکوف برگشتپذیر نامیده میشود. این شرط به صورت زیر تعریف میشود:
اگر این شرط برقرار باشد، میتوانیم بنویسیم:
رابطهٔ اخیر رابطهٔ توزیع حالت پایدار است.
خاصیت منظم بودن[ویرایش]
شرط کافی و نه لازم برای اینکه توزیع حالت پایدار زنجیرهٔ مارکف یکتا باشد؛ خاصیت منظم بودن (به انگلیسی: Regularity) آن است. زنجیرهٔ مارکف درصورت داشتن دو ویژگی زیر منظم خواهد بود[۱۱]:
- کاهشناپذیری (به انگلیسی: Irreducibility): احتمال رفتن از هر وضعیت به وضعیتهای دیگر بزرگتر از ۰ باشد.
- نامتناوب بودن (به انگلیسی: Aperiodicity): در هر لحظه از زمان امکان بازگشت به هر وضعیت وجود داشته باشد.
به عبارت دیگر در صورتی یک زنجیرهٔ مارکف دارای خاصیت منظم بودن است که حداقل یک مقدار وجود داشته باشد که به ازای هر دو وضعیت و بتوان با دقیقاً گام از وضعیت به رفت.
نحوهٔ عملکرد الگوریتم متروپلیس-هیستینگز[ویرایش]
در الگوریتم متروپلیس-هیستینگز به جای نمونهبرداری از از توزیع شرطی نمونهبرداری میکنیم و معمولاً به صورت توزیع نرمال در نظر گرفته میشود.
در این الگوریتم هر نمونهٔ که بعد از نمونهٔ تولید شده، احتمال مشخصی برای پذیرفته شدن دارد. این احتمال با نمایش داده شده و به صورت زیر محاسبه میشود:
فرایند اجرا[ویرایش]
در ابتدا به صورت تصادفی از یک وضعیت اولیه شروع میکنیم و از توزیع نمونهبرداری میکنیم و نمونهٔ را تولید میکنیم. این نمونه با احتمال پذیرفته میشود.
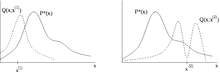
بههمین ترتیب در یک حلقه شروع به نمونهگیری از توزیع و تولید نمونهٔ میکنیم. هر نمونهٔ با احتمال شانس پذیرفته شدن دارد. دقت داریم که تابع A شامل یک کمینهگیری است و اگر مقدار پارامتر دیگر کمینهگیری بزرگتر از یک شود، تابع مقدار یک را برخواهد گرداند و نمونه حتماً پذیرفته میشود. در صورتی که مقدار پارامتر دوم کمتر از یک شود، عددی تصادفی در بازهٔ [۰٬۱] تولید میکنیم و اگر کوچکتر یا برابر با مقدار پارامتر دوم شد، نمونه را میپذیریم و در غیر این صورت نمونهٔ جدید را برابر با نمونهٔ تولید شده در مرحلهٔ قبل قرار میدهیم.
ادامه دادن این روند منجر به همگرایی توزیع زنجیرهٔ استفاده شده به توزیع اصلی (که در حال تخمین آن هستیم) خواهد شد.
نمونههایی که در این فرایند دور ریخته میشوند به عنوان نمونهٔ سوخته شناخته میشوند و در ادامهٔ فرایند الگوریتم به کار نمیآیند. مجموعهٔ باقی مانده از مقادیر مورد قبول نمونههایی از توزیع را نمایش میدهند.
در زیر شبهکدی از این الگوریتم به نمایش درآمده است.[۱۲]
initialize starting sate x(0)
set t=0
while samples have not converged:
x=x(t)
sample x* according to Q(x*|x)
A(x to x*)=min(1,[P(x*)Q(x|x*)]/[P(x)Q(x*|x)])
generate a uniform random number u from [0,1]
if u < A(x to x*):
x(t+1)=x*
else:
x(t+1)=x(t)
t=t+1
اثبات همگرایی الگوریتم متروپلیس-هیستینگز به توزیع اصلی[ویرایش]
اگر با استفاده از توزیع نمونهیرا به دست آوریم، آنگاه احتمال رفتن از وضعیت به برابر است با:
(برای حالتی که و برابر نباشند)
(برای حالتی که و برابر باشند)[۱۱]
اگر آنگاه و در نتیجه خواهد بود. در این صورت میتوانیم بنویسیم:
معادلهٔ آخر همان شرط تعادل دقیق است؛ یعنی الگوریتم متروپلیس-هیستینگز باعث میشود به یک توزیع حالت پایدار در زنجیرهٔ مارکف برسیم.
از طرف دیگر اگر باشد؛ آنگاه شرط منظم بودن زنجیرهٔ مارکف نیز برقرار است.
بنابراین این الگوریتم در نهایت به توزیع اصلی همگرا میشود.[۱۲]
مقدار مناسب برای واریانس توزیع گاوسی اولیه[ویرایش]
الگوریتم متروپلیس-هیستینگز در حالتی به بهترین نحو عمل میکند که احتمال شرطی پیشنهاد شده، با احتمالی که در حال تخمین توزیع آن هستیم (و نمونهبرداری مستقیم از آن دشوار است) مطابقت داشتهباشد؛ به عبارتی باید داشتهباشیم. اگر از یک توزیع احتمالی گاوسی برای این کار استفاده شود، باید پارامتر واریانس آن در طول فرایند انتخاب نمونههای مناسب تنظیم شود. معمولاً این کار با محاسبهٔ یک نرخ پذیرش صورت میگیرد. این نرخ نیز براساس تعداد نمونههایی که در طول تعداد دفعات مشخصی از نمونهگیری در گذشته مورد قبول واقع شدهاند؛ حساب میشود. مقدار نرخ پذیرش مطلوب بستگی به توزیع هدف دارد، هر چند از دید نظری نشان داده شده که نرخ پذیرش ایدهآل برای یک توزیع گاوسی تک بعدی حدود ۵۰٪ است. این مقدار هنگامی که از یک توزیع N بعدی گاوسی استفاده شود به ۲۳٪ کاهش پیدا میکند.[۱۳]

اگر مقدارخیلی کوچک انتخاب شود، زنجیره با سرعت پایینی به تعادل خواهد رسید (به عبارت دیگر نرخ پذیرش بالا خواهد بود ولی نمونههای پیاپی گرفته شده، با سرعت پایینی در فضای دامنهٔ متغیر توزیع پخش خواهند شد و بنابراین زنجیره با سرعت پایینی به همگرا میشود). از طرفی اگرخیلی بزرگ انتخاب شود، نرخ پذیرش بسیار پایین خواهد بود؛ چرا که نمونههای پیشنهادی احتمالاً در نقاطی از دامنهٔ چگالیِ احتمال خواهند افتاد که مقدار احتمال بسیار پایینی دارد و بنابراین بسیار کوچک خواهد شد و دوباره سرعت همگرایی زنجیره بسیار پایین خواهد بود.[۱۲] با توجه به توضیحاتی که در مورد تخمینهای نظری در این زمینه ارائه شد، این که توزیع پیشنهادی را طوری تنظیم کنیم که حدود ۳۰٪ از نمونهها مورد پذیرش واقع شوند، روش مرسومی شناخته میشود.
روش نمونهگیری گیبز به عنوان حالت خاصی از الگوریتم متروپلیس-هیستینگز[ویرایش]
روش نمونهگیری گیبز حالت خاصی از الگوریتم متروپلیس-هیستینگز است که توزیع پیشنهادی که در هر گام برای نمونهبرداری استفاده میکند تنها برای متغیر م (که جزئی از متغییرهای تصادفی توزیع اصلی است) تعریف میشود و برابر است با:
با استفاده از توزیع پیشنهادی معرفی شده در الگوریتم متروپلیس-هیستینگز میتوان ثابت کرد که احتمال پذیرش هر نمونه در روش گیبز برابر ۱ است[۱۲]:
کاربرد الگوریتم متروپلیس-هیستینگز در انتگرالگیری عددی[ویرایش]
یکی از کاربردهای مرسوم الگوریتم متروپلیس-هیستینگز در محاسبهي یک انتگرال است. فضای و یک توزیع احتمالی روی و را در نظر بگیرید. الگوریتم متروپلیس-هیستینگز میتواند انتگرالی در فرم زیر را تخمین بزند:
که در آن تابعی دلخواه است. برای مثال آمارهي و توزیع احتمالی آن را که یک توزیع احتمالی حاشیهای است، در نظر بگیرید. فرض کنیم هدف تخمین برای براساس دنبالهای از باشد. را میتوانیم به صورت زیر بازنویسی کنیم:
و بنابراین تخمین میتواند با تخمین امید ریاضی مقدار تابع مشخصهیکه مقدار آن تنها هنگامی یک خواهد بود که(و درغیراینصورت صفر خواهدبود)، صورت پذیرد. به این دلیل که روی دنبالهای از محاسبه میشود؛ احتمال این که حالت با روی دنبالهای از به دست بیاید، متناسب با است، که طبق تعریف مقدار کوچکی خواهد بود. الگوریتم متروپلیس-هیستینگ میتواند در اینجا برای نمونهگیری از حالتهایی که نادر هستند استفاده شود و آنها را با احتمال بالاتری تولید کند که منجر به افزایش تعداد نمونههای مورد استفاده برای تخمین خواهدشد. این روش میتواند به عنوان مثال با استفاده از یک توزیع مولد نمونه مثل که بیشتر به آن حالتها شانس تولید میدهد، پیادهسازی شود (برای مثال میتواند به شکل با تعریف شود).[۱]
منابع[ویرایش]
- ↑ ۱٫۰ ۱٫۱ ۱٫۲ ۱٫۳ *مشارکتکنندگان ویکیپدیا. «Metropolis–Hastings algorithm». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۵ دسامبر ۲۰۱۲.
- ↑ Hastings, W.K. (1970). "Monte Carlo Sampling Methods Using Markov Chains and Their Applications". Biometrika. 57 (1): 97–109. Bibcode:1970Bimka..57...97H. doi:10.1093/biomet/57.1.97. JSTOR 2334940. Zbl 0219.65008
- ↑ «روش پیش فرض رائو-بلکولیزه کردن الگوریتمهای متروپلیس- هستینگز».
- ↑ M.N. Rosenbluth (2003). "Genesis of the Monte Carlo Algorithm for Statistical Mechanics". AIP Conference Proceedings. 690: 22–30. doi:10.1063/1.1632112.
- ↑ J.E. Gubernatis (2005). "Marshall Rosenbluth and the Metropolis Algorithm". Physics of Plasmas. 12 (5): 057303. Bibcode:2005PhPl...12e7303G. doi:10.1063/1.1887186.
- ↑ Teller, Edward. Memoirs: A Twentieth-Century Journey in Science and Politics. Perseus Publishing, 2001, p. 328
- ↑ Rosenbluth, Marshall. "Oral History Transcript". American Institute of Physics
- ↑ F. Dyson (2006). "Marshall N. Rosenbluth". Proceedings of the American Philosophical Society. 250: 404.
- ↑ Yildirim، Ilker (اوت ۲۰۱۲). Bayesian Inference: Metropolis-Hastings Sampling. Department of Brain and Cognitive Sciences University of Rochester.
- ↑ ۱۰٫۰ ۱۰٫۱ "Metropolis–Hastings algorithm". Wikipedia (به انگلیسی). 2019-07-07.
- ↑ ۱۱٫۰ ۱۱٫۱ ۱۱٫۲ Probabilistic Graphical Models:Principles and Techniques. به کوشش D. Koller and N. Friedman.
- ↑ ۱۲٫۰ ۱۲٫۱ ۱۲٫۲ ۱۲٫۳ Eric Xing, Lecture 16, March 17, 2014
- ↑ Roberts, G.O.; Gelman, A.; Gilks, W.R. (1997). "Weak convergence and optimal scaling of random walk Metropolis algorithms". Ann. Appl. Probab. 7 (1): 110–120. CiteSeerX 10.1.1.717.2582. doi:10.1214/aoap/1034625254.











































![{\displaystyle E(x)\in [E,E+\Delta E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7bce935fdd4fc6a2721d4bdf95832c86c1c1630)


