نسبت پواسون
نسبت کرنش جانبی (عرضی) به کرنش محوری (طولی) را نسبت پواسون یا ضریب پواسون گویند. این نام به افتخار ریاضیدان فرانسوی سیمون دنیس پواسون (۱۷۸۱–۱۸۴۰ م) انتخاب شدهاست. ضریب پواسون را با حرف یونانی (نو) نمایش داده و مقدار آن وقتی که کرنش جانبی و کرنش محوری باشد، برابر است با:
علامت منفی به این خاطر است که این نسبت عددی مثبت شود زیرا در اکثر مواد مهندسی (به جز اکستیکها) کرنش جانبی و محوری مختلف العلامت هستند.
مقدمات[ویرایش]
نسبت پواسون اندازهای از اثر پواسون است، پدیدهای که در آن ماده تمایل دارد در راستای عمود بر جهت فشردگی منبسط شود. همینطور اگر به جای فشرده شدن، کشیده شود، ماده در راستای عمود بر کشش، منقبض خواهد شد. مثال بارزآن نازک شدن یک نوار پلاستیکی در اثر کشش است. در برخی مواد نادر، ماده عمود بر راستای فشردگی، منقبض و عمود بر راستای کشش، منبسط میشود؛ و باعث ایجاد ضریب پواسون منفی میگردد. ضریب پواسون برای مواد پایدار، ایزوتروپیک و کشسان خطی بین ۱- تا ۰ میباشد؛ و برای اغلب مواد بین ۰ تا ۰٫۵ است. برای یک مادهٔ کاملاً تراکم ناپذیر که به صورت کشسان تغییر شکل داده است، به ازای کرنشهای کوچک ضریب پواسون برابر با ۰٫۵ خواهد بود. اکثر فولادها و پلیمرهای سخت (صلب) قبل از تسلیم ضریب پواسون ۰٫۳ دارند، که این مقدار برای تغییر شکلهای بعد از تسلیم تا ۰٫۵ افزایش مییابد. لاستیک ضریب پواسونی نزدیک به ۰٫۵ دارد. ضریب پواسون چوب پنبه نزدیک یه ۰ میباشد به این معنا که انبساط جانبی بسیار اندکی هنگام فشرده شدن از خود نشان میدهد. برخی مواد از جمله: فومهای پلیمری، دارای ضریب پواسونی منفی هستند که به آن مواد "اکستیک" میگویند. بعضی مواد انیزوتروپیک مثل: نانو لولههای کربنی، میتوانندضریب پواسون بالای در برخی جهات معین داشته باشند. اگر فرض کنیم ماده در راستای محورش (محور "x" در رابطهٔ زیر) کشیده یا فشرده میشود، خواهیم داشت:
تغییرات طولی[ویرایش]

برای یک مکعب تحت کشش در راستای x با تغییر طول در جهت "x" و تغییر طول در راستای "y" و "z" کرنشهای کوچک به صورت زیر است:
اگر ضریب پواسون در کل تغییر حالت ثابت باشد، با انتگرالگیری از این روابط و با استفاده از تعریف ضریب پواسون داریم:
پس:
برای مقادیر بسیار کوچک و با تقریب درجهٔ یک خواهیم داشت:
تغییرات حجمی[ویرایش]
تغییر حجم نسبی ΔV/V یک مکعب که تحت کشش است اکنون قابل محاسبه است: با استفاده از و :
و برای مقادیر بسیار کوچک و با تقریب درجهٔ یک خواهیم داشت:
و برای مواد ایزوتروپ میتوانیم از رابطهٔ لامه[۱] استفاده کنیم:
که مدول بالک است.
تغییرات ضخامت[ویرایش]
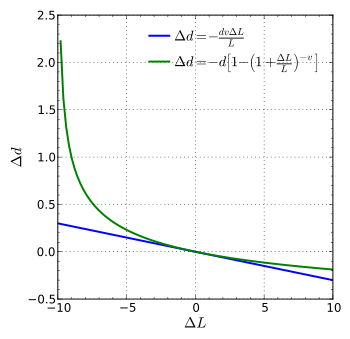
اگر میلهای با قطر (یا ضخامت) "d" و طول "L" تحت کشش باشد و طول آن به مقدار ΔL تغییر کند؛ قطر آن به مقدار زیر تغییر خواهد کرد:
رابطهٔ بالا تنها زمانی قابل استفاده است که تغییر شکل کوچک باشد. اگر تغییر شکل بزرگ بود، رابطهٔ زیر دقیق تر است:
مقدار ضریب پواسون برای مواد مختلف[ویرایش]
| مواد | ضریب پواسون |
|---|---|
| لاستیک | ۰٫۴۹۹۹ |
| طلا | ۰٫۴۲–۰٫۴۴ |
| رس اشباع | ۰٫۴۰–۰٫۴۹ |
| منیزیم | ۰٫۲۵۲–۰٫۲۸۹ |
| تیتانیوم | ۰٫۲۶۵–۰٫۳۴ |
| مس | ۰٫۳۳ |
| آلومینیوم-آلیاژ | ۰٫۳۲ |
| رس | ۰٫۳۰–۰٫۴۵ |
| فولاد ضدخش | ۰٫۳۰–۰٫۳۱ |
| فولاد | ۰٫۲۷–۰٫۳۰ |
| چدن | ۰٫۲۱–۰٫۲۶ |
| شن | ۰٫۲۰–۰٫۴۵ |
| بتن | ۰٫۱–۰٫۳ |
| شیشه | ۰٫۱۸–۰٫۳ |
| فوم | ۰٫۱۰–۰٫۵۰ |
| چوب پنبه | ۰٫۰ |
ضریب پواسون منفی[ویرایش]
ضریب پواسون منفی ابتدا در سال ۱۹۴۷ میلادی توسط Love گزارش شد. در آنزمان عقیده بر آن بود که مواد با ضریب پواسون منفی دست یافتنی نیستند و این پدیده به عنوان یک نقص در کریستال سولفید آهن خاطر نشان گردید.[۲] در ۱۹۸۷ Lakes ضریب پواسون منفی را در فومهای پلییورتان کشف کرد.[۳]
تعداد کمی مواد با ضریب پواسون منفی به صورت طبیعی وجود دارند. یک مثال از مواد اکستیک طبیعی استخوان است. ضریب پواسون منفی استخوان نخست توسط Williams و Evans اندازهگیری شد.[۴][۵]
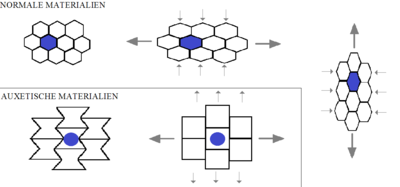
اکستیکها (به انگلیسی: Auxetics) موادی با ضریب پواسون منفی هستند. اکستیکها در هنگام اعمال تنش کششی عمودی، برخلاف مواد معمول، در راستای عمود بر نیروی وارده، ضخیمتر میشوند.[۳] این خاصیت در کامپوزیتهای لایهای،[۶] فومهای پلیمری و فلزی[۷] دیدهشدهاست. جامدات اتمی با ساختار مکعبی هنگامی که در جهت [۱۱۰] کشیده شوند نیز چنین رفتاری از خود نشان میدهند.[۸]
مواد اکستیک از لحاظ نحوه تشکیل به چهار دسته تقسیمبندی میشوند.[۹]
۱-جامدات با ساختار سلولی
۲-پلیمرهای ریزحفره Microporous material اکستیک
۳-کامپوزیتهای اکستیک
۴-مواد اکستیک مولکلی
کاربرد اثر پواسون[ویرایش]
یکی از حوزههایی که اثر پواسون در آن اثر بسزایی دارد، جریان تحت فشار درون لوله هاست. هنگامی که هوا یا مایع درون یک لوله به شدت تحت فشار باشد، نیروی یکنواختی را به سطح داخلی لوله اعمال میکند که باعث ایجاد تنش حلقوی در لوله میشود. به دلیل اثر پواسون این تنش حلقوی باعث افزایش قطر لوله و اندکی کاهش طول آن میگردد. این کاهش طول میتواند تأثیر بسیار زیادی در اتصالات لوله داشته باشد؛ که حتی میتواند باعث جدا شدن اتصالات شود.
دیگر کاربرد اثر پواسون در زمینهٔ زمینشناسی ساختاری است. سنگها نیز همانند بسیاری از مواد هنگامی که تحت تنش قرارمیگیرند اثر پواسون در آنها نمایان میگردد. فرسایش بیش از حد یا رسوب گذاری پوستهٔ زمین میتواند باعث ایجاد یا از بین رفتن مقدار زیادی تنش عمودی روی سنگهای زیرین گردد. این امر باعث منبسط یا منقبض شدن سنگ در راستای عمودی میگردد و به علت اثر پواسون در راستای افقی نیز تغییر شکل میدهد.[۱۰]
استفادهٔ چوب پنبه به عنوان در بطری نوشیدنیها به علت ضریب پواسون نزدیک به صفر آن است؛ بنابراین هنگامی که چوب پنبه وارد بطری میشود بخش بالایی از آن که هنوز وارد بطری نشدهاست افزایش قطر نمیدهد؛ در حالی که در راستای محورش فشرده شدهاست. نیروی لازم برای وارد کردن چوب پنبه به داخل بطری تنها به علت اصطکاک بین چوب پنبه و در بطری است؛ که به علت فشردگی شعاعی ایجاد میشود. برای مثال: اگر درب بطری از لاستیک ساخته میشداحتیاج به نیروی نسبتاً بزرگی برای غلبه بر انبساط شعاعی آن در بالایی درب میبود.
منابع[ویرایش]
- ↑ http://arxiv.org/ftp/arxiv/papers/1204/1204.3859.pdf - Limits to Poisson’s ratio in isotropic materials – general result for arbitrary deformation.
- ↑ A.E.H. Love, A treatise on the mathematical theory of elasticity, (Dover,1944) 4th ed.
- ↑ ۳٫۰ ۳٫۱ Roderic Lakes, Foam structures with a negative Poisson’s ratio, Science Vol. 235 (1987), pp. 1038-1040 doi:10.1126/science.235.4792.1038
- ↑ Williams JL, Lewis JL. Properties and an anisotropic model of cancellous bone from the proximal tibial epiphyris. Journal of Biomechanical Engineering 1982; 104(1): 50-56.
- ↑ Evans KE (1990). Tailoring the negative Poisson's ratio. Chemistry and Industry 1990; 20: 654-657
- ↑ Graeme W. Milton, Composite materials with poisson's ratios close to — 1, Journal of the Mechanics and Physics of Solids, Vol. 40 (1992), pp. 1105-1137. doi:10.1016/0022-5096(92)90063-8
- ↑ E. A. Friis, R. S. Lakes, and J. B. Park, Negative Poisson's ratio polymeric and metallic foams, Journal of Materials Science, Vol. 23 (1988), pp. 4406-4414. doi:10.1007/BF00551939
- ↑ Ray H. Baughman, Justin M. Shacklette, Anvar A. Zakhidov, Sven Stafström, Negative Poisson's ratios as a common feature of cubic metals, Nature, Vol. 392 (1998), pp. 362-365. doi:10.1038/32842
- ↑ Yang W, Li Z, Shi W, Xie B and Yang M , Review on auxetic materials , Journal of materials science 39 (2004) 3269-3279
- ↑ http://www.geosc.psu.edu/~engelder/geosc465/lect18.rtf
| رابطههای تبدیل مدولها به یکدیگر | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| خواص کشسانی مواد کشسان خطی همگن و همسانگرد را میتوان با داشتن دو مدول دلخواه به طور کامل و منحصر به فردی تعیین کرد. بنابراین با در دست داشتن دو مدول و با استفاده از فرمولهای زیر میتوان سایر مدولها را محاسبه کرد. | ||||||||||
| توضیحات | ||||||||||
There are two valid solutions. | ||||||||||
| Cannot be used when | ||||||||||














































































































