روش نلدر-مید

روش نلدر-مید (به انگلیسی: Nelder-Mead method) یا روش سیمپلکس سراشیبی، یک روش عددی رایج در پیدا کردن کمینه یا بیشینه یک تابع هدف در فضای بهینه‌سازی چند بعدی می‌باشد. این یک روش جستجوی مستقیم (بر اساس مقایسه عملکرد) است و اغلب برای مشکلات بهینه‌سازی غیرخطی است که مشتقات آن ممکن است مشخص نباشد، استفاده می‌شود. با این حال، تکنیک Nelder-Mead یک روش جستجوی اکتشافی است که می‌تواند به نقاط غیر ثابت،^[۱] در مورد مسائلی که می‌توان با روشهای جایگزین حل گردد، همگرا شود.^[۲]

روش نلدر-مید توسط جان نلدر و راجر مید در سال ۱۹۶۵ پیشنهاد شد،^[۳] که به عنوان توسعه ای از روش Spendley و همکاران بود.^[۴]

بررسی اجمالی[ویرایش]

در این روش از مفهوم سیمپلکس استفاده شده‌است، که یک چندبر ویژه با n+1 راس در یک n بعدی می‌باشد. نمونه‌هایی از سیمپلکس‌ها عبارتند از: یک پاره خط بر روی یک خط، یک مثلث در صفحه، یک چهار وجهی در فضای سه بعدی و غیره.

هنگامی که تابع هدف به نرمی تغییر می‌کند و یکتا می‌باشد، این روش یک بهینه‌سازی محلی برای یک مسئله با n متغیر را تقریب می‌کند. پیاده‌سازی‌های معمولی توابع را به حداقل می‌رسانند، یا با به کمینه کردن $-f(\mathbf {x} )$ ، $f(\mathbf {x} )$ را بیشینه می‌کنند.

به عنوان مثال، در یک پل تعلیق مهندس باید انتخاب کند که هر بند، کابل و اسکله چقدر ضخیم باشد. این عناصر به هم وابسته هستند، اما تجسم تأثیر تغییر هر عنصر خاص کار ساده ای نیست. شبیه‌سازی چنین ساختارهای پیچیده‌ای از لحاظ محاسباتی اغلب پر هزینه بوده و احتمالاً ساعت‌ها برای اجرای آن طول می‌کشد. روش Nelder-Mead، در نوع اصلی نیاز به بیش از دو ارزیابی در هر تکرار ندارد، به جز عملیات منقبض شدن که در ادامه شرح داده شده‌است، که در مقایسه با برخی دیگر از روش‌های بهینه‌سازی جستجوی مستقیم، مورد توجه است. با این حال، مجموع تعداد تکرارها، ممکن است از حد مطلوب پیشنهادی بیشتر باشد.

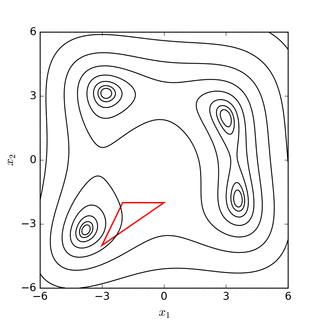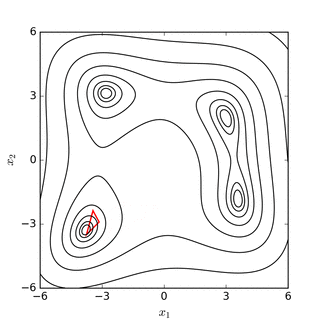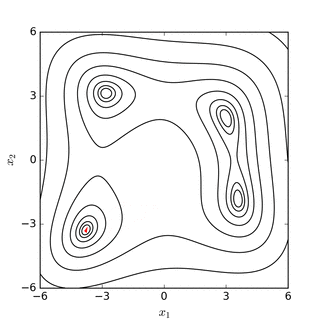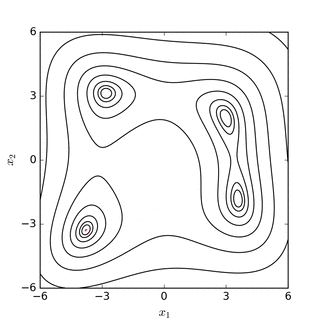
روش نلدر – مید در یک مسئله n بعدی، مجموعه از n+1 نقطه آزمایشی که به صورت سیمپلکس است را در نظر می‌گیرد. سپس به منظور پیدا کردن یک نقطه آزمایشی جدید و جایگزینی یکی از نقاط آزمایشی قدیمی با مورد جدید، رفتا تابع مورد نظر در هر نقطه آزمایشی، مورد بررسی قرار می‌گیرد و سپس این روش ادمه پیدا می‌کند. ساده‌ترین رویکرد جایگزینی بدترین نقطه، از لحاظ مقدار، با یک نقطه منعکس شده، از طریق مرکز n نقطه باقی مانده می‌باشد. اگر این نقطه منعکس شده بهتر از نقطه فعلی باشد، می‌توانیم کشیدگی را در امتداد این خط امتحان کنیم. از طرفی دیگر، اگر این نکته جدید بهتر از مقدار نقطه قبلی نباشد، در واقع ما در یک دره قدم می‌گذاریم، بنابراین سیمپلکس را در جهت بدست آوردن یک نقطه بهتر منقبض می‌کنیم. توضیح شهودی الگوریتم از "دستور العمل‌های عددی":^[۵]

روش سرازیر سیمپلکس یک سری مراحل را طی می‌کند به طوریکه بیشتر مراحل فقط نقاط سیمپلکس را در جایی که خروجی تابع بیشینه است، از طریق نقطه مقابل سیمپلکس، به یک نقطه کمینه انتقال می‌دهد. این مراحل بازتاب نامیده می‌شوند، و برای حفظ حجم سیمپلکس ساخته می‌شوند. وقتی این مراحل انجام می‌شود، سیمپلکس در جهت یا جهت دیگر گسترش می‌یابد تا گام‌های بزرگتری برداشته شود. هنگامی که به «کف دره» رسید، این روش خود را در جهت عرضی منقبض می‌کند و سعی می‌کند از دره بیرون رود. اگر شرایطی وجود داشته باشد که سیمپلکس سعی کند «از چشم سوزن عبور کند»، خود را از همه جهات منقبض می‌کند، و خود را به پایین‌ترین (بهترین) نقطه می‌کشد.

بر خلاف روش‌های بهینه‌سازی مدرن، روش اکتشافی نلدر-مید می‌تواند به یک نقطه غیر ثابت همگرا شود، مگر اینکه این ممسئله شرایط قوی تری از آنچه برای روش‌های نوین لازم است را برآورده کند.^[۱] بهبودهای جدیدی بر روش اکتشافی نلدر-مید از سال ۱۹۷۹ شناخته شده‌است.^[۲]

بسته به ماهیت واقعی مسئله حل شده، تغییرات زیادی وجود دارد. یک نوع رایج از یک سیمپلکس کوچک با اندازه ثابت استفاده می‌کند که تقریباً از جهت شیب پیروی می‌کند. این روش همچنین به عنوان روش چندضلعی انعطاف‌پذیر شناخته می‌شود.

حالتی از الگوریتم ممکن برای NM[ویرایش]

هدف ما به حداقل رساندن تابع $f(\mathbf {x} )$ می‌باشد، جایی که $\mathbf {x} \in \mathbb {R} ^{n}$ . نقاط آزمایشی فعلی ما $\mathbf {x} _{1},\ldots ,\mathbf {x} _{n+1}$ هستند.

۱. مرتب‌سازی با توجه به مقادیر تابع در رئوس:

f(\mathbf {x} _{1})\leq f(\mathbf {x} _{2})\leq \cdots \leq f(\mathbf {x} _{n+1}).

بررسی کنید که آیا روش باید متوقف شود. خاتمه را در زیر مشاهده کنید. گاهی اوقات به گونه ای نامناسب «همگرایی» خوانده می‌شود.

۲. محاسبه $\mathbf {x} _{o}$ ، که مرکز همه نقاط به جز $\mathbf {x} _{n+1}$ می‌باشد.

۳. بازتاب

محاسبه نقطه منعکس شده

\mathbf {x} _{r}=\mathbf {x} _{o}+\alpha (\mathbf {x} _{o}-\mathbf {x} _{n+1})

با

\alpha >0

.

اگر نقطه منعکس شده

f(\mathbf {x} _{1})\leq f(\mathbf {x} _{r})<f(\mathbf {x} _{n})

،

سپس با جایگزین کردن بدترین نقطه

\mathbf {x} _{n+1}

، با نقطه منعکس شده

\mathbf {x} _{r}

، سیمپلکس جدید را به دست آورید و به مرحله ۱ بازگردید.

۴. گسترش

اگر نکته منعکس شده بهترین نقطه تا کنون است،

f(\mathbf {x} _{r})<f(\mathbf {x} _{1})

،

سپس نقطه گسترش یافته را محاسبه کنید

\mathbf {x} _{e}=\mathbf {x} _{o}+\gamma (\mathbf {x} _{r}-\mathbf {x} _{o})

با

\gamma >1

.

اگر نقطه گسترش یافته بهتر از نقطه منعکس شده باشد،

f(\mathbf {x} _{e})<f(\mathbf {x} _{r})

،

سپس با جایگزین کردن بدترین نکته

\mathbf {x} _{n+1}

، با نقطه گسترش یافته

\mathbf {x} _{e}

سیمپلکس جدید را بدست آورید و به مرحله ۱ بروید؛:: در غیر اینصورت با جایگزین کردن بدترین نکته

\mathbf {x} _{n+1}

، با نکته منعکس شده

\mathbf {x} _{r}

سیمپلکس جدید را بدست آورید و به مرحله ۱ بروید.

۵. انقباض

در اینجا مسلم است که

f(\mathbf {x} _{r})\geq f(\mathbf {x} _{n})

. (توجه داشته باشید که

\mathbf {x} _{n}

دوم یا بالاترین «بعدی» است)

محاسبه نقطه انقباض شده

\mathbf {x} _{c}=\mathbf {x} _{o}+\rho (\mathbf {x} _{n+1}-\mathbf {x} _{o})

با

0<\rho \leq 0.5

.

اگر نقطه انقباض شده بهتر از بدترین نقطه باشد، یعنی

f(\mathbf {x} _{c})<f(\mathbf {x} _{n+1})

،

سپس با جایگزین کردن بدترین نکته

\mathbf {x} _{n+1}

، با نقطه انقباض شده

\mathbf {x} _{c}

سیمپلکس جدید را بدست آورید و به مرحله ۱ بروید.

۶. کوچک شدن

همه نقاط را به جز بهترین (

\mathbf {x} _{1}

) با

\mathbf {x} _{i}=\mathbf {x} _{1}+\sigma (\mathbf {x} _{i}-\mathbf {x} _{1})

جایگزین کنید و به مرحله ۱ بروید.

توجه: $\alpha$ ، $\gamma$ ، $\rho$ و $\sigma$ ضرایب بازتاب، گسترش، انقباض و کوچکی هستند. مقادیر استاندارد $\alpha =1$ ، $\gamma =2$ ، $\rho =1/2$ و $\sigma =1/2$ هستند.

برای بازتاب، از آن زمان که $\mathbf {x} _{n+1}$ راس با ارزش بالاتر در بین رئوس است، می‌توان انتظار داشت که در بازتاب، $\mathbf {x} _{n+1}$ مقدار کمتری داشته باشد که توسط همه راسها $\mathbf {x} _{i}$ جز $\mathbf {x} _{n+1}$ در طرف مخالف شکل گرفته‌است.

برای گسترش، اگر نقطه بازتاب $\mathbf {x} _{r}$ کمینه جدید در بین رئوس باشد، می‌توان انتظار داشت که مقادیر جالبی را در طول مسیر از $\mathbf {x} _{o}$ به $\mathbf {x} _{r}$ پیدا کنیم.

در مورد انقباض، اگر $f(\mathbf {x} _{r})>f(\mathbf {x} _{n})$ باشد، می‌توان انتظار داشت که یک مقدار بهتر در بین سیمپلکس تشکیل شده توسط همه راسها $\mathbf {x} _{i}$ باشد.

در نهایت، کوچک شدن یک مورد نادر است، که انقباض از بزرگترین نقطه ای که $f$ افزایش می‌یابد، اتفاق می‌افتد. اتفاقی که نمی‌تواند به اندازه کافی نزدیک به یک حداقل غیر تکین رخ دهد. در این صورت در انتظار یافتن دورنمایی ساده‌تر انقباض می‌یابد که به پایین‌ترین نقطه می‌رسیم. با این حال، نش اشاره می‌کند که با دقت محدود عددی گاهی اوقات نمی‌تواند در کوچک کردن سیمپلکس عمل کند، و بررسی ای را انجام داد که اندازه در واقع کاهش یافته‌است.^[۶]

سیمپلکس اولیه[ویرایش]

سیمپلکس اولیه بسیار مهم است. در واقع، یک سیمپلکس اولیه خیلی کوچک می‌تواند به جستجوی محلی منجر شود، در نتیجه NM می‌تواند به راحتی جوابگو نباشد؛ بنابراین این سیمپلکس باید بستگی به ماهیت مسئله داشته باشد. با این حال، مقاله اصلی سیمپلکس ای را پیشنهاد می‌کند که یک نقطه اولیه به عنوان $\mathbf {x} _{1}$ داده می‌شود، همراه با نقاط دیگر که با یک گام ثابت در طول هر بعد تولید می‌شود؛ بنابراین روش به مقیاس متغیرهای که $\mathbf {x}$ را تشکیل می‌دهد، حساس است.

شرط خاتمه[ویرایش]

معیارهایی برای شکستن چرخه تکراری لازم است. نلدر و مید از انحراف استاندارد برای مقادیر تابع، به ازای سیمپلکس فعلی استفاده کردند. اگر مقادیر تابع کوچکتر از یک مقدار معین گردد، چرخه متوقف می‌شود و پایین‌ترین نقطه در سیمپلکس به عنوان یک نقطه بهینه پیشنهادی بازمی‌گردد. توجه داشته باشید که یک تابع بسیار «مسطح» ممکن است مقادیر عملکرد تقریباً برابر با یک دامنه بزرگ داشته باشد، به طوری که جواب به مقدار تلرانس حساس خواهد بود. نش آزمایشی برای shrinkage به عنوان یکی دیگر از معیارهای خاتمه اضافه می‌کند.^[۶] توجه داشته باشید که برنامه‌ها خاتمه می‌یابند، در حالی که تکرارها ممکن است همگرا شوند.

جستارهای وابسته[ویرایش]

Derivative-free optimization
COBYLA
NEWUOA
LINCOA
Nonlinear conjugate gradient method
Levenberg–Marquardt algorithm
Broyden–Fletcher–Goldfarb–Shanno or BFGS method
Differential evolution
Pattern search (optimization)
CMA-ES

منابع[ویرایش]

↑ ^۱٫۰ ^۱٫۱
* Powell, Michael J. D. (1973). "On Search Directions for Minimization Algorithms". Mathematical Programming. 4: 193–201. doi:10.1007/bf01584660.
- McKinnon, K. I. M. (1999). "Convergence of the Nelder–Mead simplex method to a non-stationary point". SIAM Journal on Optimization. 9: 148–158. CiteSeerX 10.1.1.52.3900. doi:10.1137/S1052623496303482. (algorithm summary online).
↑ ^۲٫۰ ^۲٫۱
* Yu, Wen Ci. 1979. "Positive basis and a class of direct search techniques". Scientia Sinica [Zhongguo Kexue]: 53—68.
- Yu, Wen Ci. 1979. "The convergent property of the simplex evolutionary technique". Scientia Sinica [Zhongguo Kexue]: 69–77.
- Kolda, Tamara G.; Lewis, Robert Michael; Torczon, Virginia (2003). "Optimization by direct search: new perspectives on some classical and modern methods". SIAM Rev. 45 (3): 385–482. CiteSeerX 10.1.1.96.8672. doi:10.1137/S003614450242889.
- Lewis, Robert Michael; Shepherd, Anne; Torczon, Virginia (2007). "Implementing generating set search methods for linearly constrained minimization". SIAM J. Sci. Comput. 29 (6): 2507–2530. CiteSeerX 10.1.1.62.8771. doi:10.1137/050635432.
↑ Nelder, John A.; R. Mead (1965). "A simplex method for function minimization". Computer Journal. 7 (4): 308–313. doi:10.1093/comjnl/7.4.308.
↑ Spendley, W.; Hext, G. R.; Himsworth, F. R. (1962). "Sequential Application of Simplex Designs in Optimisation and Evolutionary Operation". Technometrics. 4 (4): 441–461. doi:10.1080/00401706.1962.10490033.
↑ * Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). "Section 10.5. Downhill Simplex Method in Multidimensions". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Archived from the original on 11 August 2011. Retrieved 22 November 2019.
↑ ^۶٫۰ ^۶٫۱ Nash, J. C. (1979). Compact Numerical Methods: Linear Algebra and Function Minimisation. Bristol: Adam Hilger. ISBN 978-0-85274-330-0.

خواندن بیشتر[ویرایش]

Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 978-0-486-43227-4.
Coope, I. D.; Price, C. J. (2002). "Positive Bases in Numerical Optimization". Computational Optimization & Applications. 21 (2): 169–176. doi:10.1023/A:1013760716801.
Gill, Philip E.; Murray, Walter; Wright, Margaret H. (1981). "Methods for Multivariate Non-Smooth Functions". Practical Optimization. New York: Academic Press. pp. 93–96. ISBN 978-0-12-283950-4.
Kowalik, J.; Osborne, M. R. (1968). Methods for Unconstrained Optimization Problems. New York: Elsevier. pp. 24–27. ISBN 0-444-00041-0.
Swann, W. H. (1972). "Direct Search Methods". In Murray, W. (ed.). Numerical Methods for Unconstrained Optimization. New York: Academic Press. pp. 13–28. ISBN 978-0-12-512250-4.

پیوند به بیرون[ویرایش]

توضیح و تجسم نلدر مید (Downhill Simplex) با عملکرد موز روزنزبروک
جان بورکارد: کد نلدر-مید در ماتلب - توجه داشته باشید که تغییر روش Nelder-Mead نیز توسط fminsearch عملکرد Matlab انجام شده‌است.
بهینه‌سازی Nelder-Mead در پایتون در کتابخانه SciPy.
nelder-mead - اجرای پایتون از روش Nelder-Mead -
SOVA 1.0 (نرم‌افزار رایگان) - بهینه‌سازی ساده برای کاربردهای مختلف
[۱] - HillStormer، ابزاری عملی برای بهینه‌سازی ساده غیر محدود، چند متغیره و خطی توسط Nelder Mead.

[PM-1] ۱٫۰ ^۱٫۱ * Powell, Michael J. D. (1973). "On Search Directions for Minimization Algorithms". Mathematical Programming. 4: 193–201. doi:10.1007/bf01584660.
McKinnon, K. I. M. (1999). "Convergence of the Nelder–Mead simplex method to a non-stationary point". SIAM Journal on Optimization. 9: 148–158. CiteSeerX 10.1.1.52.3900. doi:10.1137/S1052623496303482. (algorithm summary online).

[2] McKinnon, K. I. M. (1999). "Convergence of the Nelder–Mead simplex method to a non-stationary point". SIAM Journal on Optimization. 9: 148–158. CiteSeerX 10.1.1.52.3900. doi:10.1137/S1052623496303482. (algorithm summary online).

[YKL-2] ۲٫۰ ^۲٫۱ * Yu, Wen Ci. 1979. "Positive basis and a class of direct search techniques". Scientia Sinica [Zhongguo Kexue]: 53—68.
Yu, Wen Ci. 1979. "The convergent property of the simplex evolutionary technique". Scientia Sinica [Zhongguo Kexue]: 69–77.

Kolda, Tamara G.; Lewis, Robert Michael; Torczon, Virginia (2003). "Optimization by direct search: new perspectives on some classical and modern methods". SIAM Rev. 45 (3): 385–482. CiteSeerX 10.1.1.96.8672. doi:10.1137/S003614450242889.

Lewis, Robert Michael; Shepherd, Anne; Torczon, Virginia (2007). "Implementing generating set search methods for linearly constrained minimization". SIAM J. Sci. Comput. 29 (6): 2507–2530. CiteSeerX 10.1.1.62.8771. doi:10.1137/050635432.

[4] Yu, Wen Ci. 1979. "The convergent property of the simplex evolutionary technique". Scientia Sinica [Zhongguo Kexue]: 69–77.

[5] Kolda, Tamara G.; Lewis, Robert Michael; Torczon, Virginia (2003). "Optimization by direct search: new perspectives on some classical and modern methods". SIAM Rev. 45 (3): 385–482. CiteSeerX 10.1.1.96.8672. doi:10.1137/S003614450242889.

[6] Lewis, Robert Michael; Shepherd, Anne; Torczon, Virginia (2007). "Implementing generating set search methods for linearly constrained minimization". SIAM J. Sci. Comput. 29 (6): 2507–2530. CiteSeerX 10.1.1.62.8771. doi:10.1137/050635432.

[NM-3] Nelder, John A.; R. Mead (1965). "A simplex method for function minimization". Computer Journal. 7 (4): 308–313. doi:10.1093/comjnl/7.4.308.

[SHH-4] Spendley, W.; Hext, G. R.; Himsworth, F. R. (1962). "Sequential Application of Simplex Designs in Optimisation and Evolutionary Operation". Technometrics. 4 (4): 441–461. doi:10.1080/00401706.1962.10490033.

[NR-5] * Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). "Section 10.5. Downhill Simplex Method in Multidimensions". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Archived from the original on 11 August 2011. Retrieved 22 November 2019.

[CNM-6] ۶٫۰ ^۶٫۱ Nash, J. C. (1979). Compact Numerical Methods: Linear Algebra and Function Minimisation. Bristol: Adam Hilger. ISBN 978-0-85274-330-0.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]