تابع روزن‌بروک

طرح Rosenbrock تابع دو متغیر است.

در بهینه‌سازی‌های ریاضی تابع روزن‌بروک تابع غیر محدب استفاده می‌شود که توسط هاوارد اچ روزن بروک در سال ۱۹۶۰ به عنوان یک آزمون عملکرد برای بهینه‌سازی الگوریتم‌ها معرفی شده‌است. همچنین به عنوان دره روزن بروک یا Rosenbrock's banana function شناخته می‌شود.

که هدف آن پیدا کردن مینیمم و بهینه کردن تابع سهمی‌وار شکل شده تخت

شکل کلی تابع اینگونه تعریف شده‌است:

$f(x,y)=(a-x)^{2}+b(y-x^{2})^{2}$

نقطه مینیمم بهینه $(x,y)=(a,a^{2})$جایی که $f(x,y)=0$. که معمولاً $a=1$ و $b=100$.

توضیح کلیات بحث

در دو نوع معمولاً اتفاق می‌افتد اولی مجموع $N/2$ و دومی مشکلات غیر همراه 2D Rosenbrock

$f(\mathbf {x} )=f(x_{1},x_{2},\dots ,x_{N})=\sum _{i=1}^{N/2}\left[100(x_{2i-1}^{2}-x_{2i})^{2}+(x_{2i-1}-1)^{2}\right].$

این نوع دیگر که تنها تعریف شده برای هر $N$ و راه حل‌های ساده قابل پیش‌بینی.

A بیشتر درگیر نوع است

$f(\mathbf {x} )=\sum _{i=1}^{N-1}100(x_{i+1}-x_{i}^{2})^{2}+(1-x_{i})^{2}\quad {\mbox{where}}\quad \mathbf {x} =[x_{1},\ldots ,x_{N}]\in \mathbb {R} ^{N}.$

این نوع نشان داده شده‌است که دقیقاً یک حداقل $N=3$ (در $(1,1,1)$) و دقیقاً دو کمترین برای $4\leq N\leq 7$جهانی حداقل همه آنهایی که محلی حداقل در نزدیکی $(x_{1},x_{2},\dots ,x_{N})=(-1,1,\dots ,1)$. این نتیجه به دست آمده است با تنظیم شیب تابع برابر صفر توجه است که در نتیجه معادله یک تابع منطقی $x$است. برای $N$ چندجمله‌ای تعیین می‌شود و دقیقاً قضیه استورم می‌تواند مورد استفاده برای تعیین تعداد ریشه‌های واقعی در حالی که ریشه‌ها را می‌توان محدود در منطقه $|x_{i}|<2.4$است. برای بزرگتر $N$ این روش معافیت‌های پایین با توجه به اندازه ضرایب درگیر است.

نقاط ثابت

بسیاری از نقاط ثابت از تابع نشان یک الگوی منظم که رسم شده‌است؛ که این ساختار می‌تواند برای آن‌ها را بیابید.

Rosenbrock ریشه‌های برگزاری نمایشگاه قوز سازه

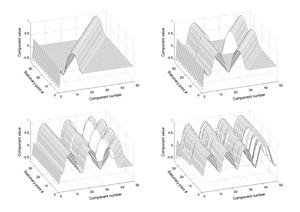
به عنوان مثال بهینه‌سازی

این تابع روزن بروک می‌تواند کارآمد بهینه‌سازی شده توسط تطبیق مناسب و هماهنگ کردن سیستم بدون استفاده از هر گونه شیب اطلاعات و بدون ساختمان محلی تقریب (در مقایسه با بسیاری از derivate-رایگان بهینه). شکل زیر نشان می‌دهد به عنوان مثال از ۲ بعدی Rosenbrock تابع بهینه‌سازی توسط تطبیقی هماهنگ تبار از نقطه شروع $x_{0}=(-3,-4)$. این راه حل با مقدار تابع را $10^{-10}$ می‌توان پس از ۳۲۵ تابع ارزیابی است.

جستارهای وابسته

• تست برای بهینه‌سازی توابع

منابع

• Rosenbrock, H. H. (1960), "An automatic method for finding the greatest or least value of a function", The Computer Journal, 3: 175–184, doi:10.1093/comjnl/3.3.175, ISSN 0010-4620, MR 0136042

پیوند به بیرون

• Rosenbrock رسم تابع در 3D
• به حداقل رساندن Rosenbrock تابع توسط مایکل Croucher با Wolfram Demonstrations Project.
• Weisstein, Eric W. "Rosenbrock Function". MathWorld.