استنباط بیزی تبارزایش

استنباط بیزی فیلوژنی از تابع درست نمایی برای ایجاد کمیتی به نام احتمال پسین درخت‌ها (درخت‌های فیلوژنی) استفاده می‌کند. محتمل‌ترین درخت فیلوژنتیک برای داده‌های داده شده با استفاده از مدل فرگشت و بر اساس احتمالات پیشین تولید خواهد شد. دلیل محبوبیت رویکرد بیزی، پیشرفت سرعت محاسبات و یکپارچه الگوریتم‌های زنجیره مارکوف مونت کارلو (MCMC) می‌باشد. استنباط بیزی در فیلوژنتیک مولکولی و سیستماتیککاربرد دارد.

ریشه و اساس استنباط بیزی فیلوژنی

قضیه بیز

تصویر نشان دادن مراحل روش MCMC

استنباط بیزی روش احتمالی توسعه یافته مبتنی بر قضیه بیز می‌باشد که توسط توماس بیز ارائه شده‌است. استنباط بیزی در سال ۱۷۶۳ پس از مرگ بیز منتشر شده‌است. این اولین بیان احتمال معکوس و اساس استنباط بیزی می‌باشد. پی یر سیمون لاپلاس به‌طور مستقل و بدون آگاهی از کار بیز، قضیه بیز را در سال ۱۷۷۴ توسعه داده است.

استنباط بیزی تا سال ۱۹۰۰ به دلیل محدودیت محاسبات به‌طور گسترده‌ای استفاده می‌شد. در سال ۱۹۰۰ شاهد انتقال از استنباط بیزی به استنباط فراوانی‌گرایانه بودیم. بر اساس قضیه بیز رویکرد بیزی احتمال پیشین درخت P(A) را با احتمال درست نمایی داده P(B) ترکیب می‌کند تا توزیع احتمال پسین P(A|B) را روی درخت تولید کند. احتمال پسین درخت، احتمال درست بودن درخت را نشان می‌دهد. درخت با بالاترین احتمال پسین، بهترین گزینه برای نمایش فیلوژنی است. استنباط بیز مقدمه‌ای برای روش‌های زنجیره مارکوف مونت کارلو (MCMC) بود که توسط نیکولاس متروپلیس در سال ۱۹۵۳ عرضه شد. این روش استنباط بیزی منقلب شده‌است و phylogeneticistها تا دهه 1990s به‌طور گسترده‌ای از این روش استفاده کردند. از مزایای ای روش نسبت به روش‌های مرسوم بیشینه صرفه جویی و بیشینه درست نمایی می‌توان به امکان عدم قطعیت فیلوژنتیک، استفاده از اطلاعات پیشین و اختلاط مدل‌های پیچیده تکامل اشاره کرد که برای روش‌های مرسوم محدودیت تحلیل‌های محاسباتی دارند. با وجود غلبه بر پیچیدگی عملیات تحلیلی احتمال پسین، هنوز شامل پیچیدگی جمع روی تمام درختان است و برای هر درخت ادغام تمام ترکیبات جایگزینی مقادیر پارامتر مدل و طول انشعاب‌ها.

روش MCMC را می‌توان در سه مرحله توصیف کرد: اول با استفاده از مکانیزم تصادفی حالت جدید برای زنجیره مارکوف پیشنهاد می‌شود. دوم، احتمال درست بودن حالت جدید محاسبه می‌شود. سوم، یک متغیر تصادفی جدید در بازه (۰٬۱) پیشنهاد می‌شود. اگر این مقدار جدید کمتر از احتمال پذیرش باشد، حالت جدید پذیرفته شده‌است و حالت زنجیره آپدیت می‌شود. این فرایند هزاران یا میلیون‌ها بار اجرا می‌شود. مقدار زمانی که یک درخت مجزا در طول زنجیره‌ای مشاهده می‌شود تقریب معتبری از احتمال پسین آن می‌باشد. تعدادی از رایج‌ترین الگوریتم‌های مورد استفاده در روش‌های MCMC شامل الگوریتم متروپلیس‌هستینگز، MCMCMC (MC³) و الگوریتم محلی لارگت و سیمون می‌باشد.

الگوریتم متروپلیس‌هستینگز

یکی از رایج‌ترین روش‌های MCMC مورد استفاده در الگوریتم متروپلیس‌هستینگز نسخه اصلاح شده از الگوریتم اصلی متروپلیس می‌باشد. برای نمونه برداری تصادفی از توزیع‌های احتمالاتی پیچیده و چند بعدی به صورت گسترده استفاده می‌شود. الگوریتم متروپلیس طبق مراحل زیر توصیف می‌شود:

1. درخت اولیه T_i است که به‌طور تصادفی انتخاب می‌شود.
2. درخت همسایه T_j از مجموعه‌ای از درختان انتخاب می‌شود.
3. نسبت R از احتمالات (یا توابع چگالی احتمال) از T_j و T_i به این صورت محاسبه می‌شود: R = f(T,_j)/f(T_i)
4. اگر R ≥ 1, T_j به عنوان زمان فعلی پذیرفته می‌شود.
5. اگر R < 1, T_j با احتمال R به عنوان درخت فعلی پذیرفته می‌شود در غیر این صورت T_i به عنوان درخت فعلی باقی خواهد ماند.
6. در این مرحله فرایند از مرحله ۲، N بار تکرار می‌شود.

الگوریتم تاز مانی که به توزیع متوازن (متعادل) برسد اجرا خواهد شد. همچنین فرض کرده‌ایم احتمال پیشنهاد درخت جدید Tj، زمانی که ما در درخت حالت قدیم Ti هستیم با احتمال پیشنهاد T_i هنگامی که ما در T_j هستیم یکسان است. اگر این مورد درست نباشد، تصحیح‌های هستینگز اعمال می‌شوند. هدف از الگوریتم متروپلیس‌هستینگز تولید مجموعه‌ای از حالات با توزیع معین است تا زمانی که فرایند مارکف به توزیع مانا برسد. الگوریتم دو جزء دارد:

1. پتانسیل انتقال از یک حالت به حالت دیگر (i→ j) با استفاده از تابع انتقال احتمال q_i,j
2. حرکت زنجیره به حالت j با احتمال α_i,j و ماندن در حالت i با احتمال ۱ – α_i,j.

MCMCMC

الگوریتم MCMCMC (MC³) برای حل نگرانی‌های عملی از مدل زنجیره مارکوف در حال حرکت در سراسر قله‌ها مطرح شده‌است. وقتی که می‌دانیم در فضای درخت توزیع هدف قله‌های محلی (ماکزیمم محلی) متعددی دارد که با دره‌های کم عمق (مینیمم محلی) از هم جدا شده‌اند. این مورد در طول درخت جستجوی اکتشافی تحت بیشینه صرفه جویی (MP)، بیشینه درست نمایی (ML) و معیار حداقل تکامل (ME) و همان را می‌توان برای درخت جستجوی تصادفی با استفاده از MCMC انتظار داشت. نتیجه این مشکل در نمونه‌هایی که به درستی چگالی پسین را تخمین نمی‌زنند خود را نشان می‌دهد. الگوریتم (MC3) ترکیب زنجیره مارکف در حضور قله‌های متعدد محلی در چگالی پسین را بهبود می‌بخشد. زنجیره‌های موازی چندگانه (m) را اجرا می‌کند، برای هر کدام n تکرار و با توزیع‌های مانای مختلف $\pi _{j}(.)$با $j=1,2,...,m$که در آن اولین، $\pi _{1}=\pi$ چگالی هدف است و $\pi _{j}$ با $j=2,3,...,m$ برای بهبود ترکیب انتخاب شده‌اند. برای مثال می‌توان گرمایش افزایشی به فرم زیر را انتخاب کرد:

$\pi _{j}(\theta )=\pi (\theta )^{1/[1+\lambda (j-1)]},\ \ \lambda >0,$

به طوری که اولین زنجیر، زنجیره سرد با چگالی هدف درست است، در حالی که زنجیرهای $2,3,...,m$ زنجیرهای گرم هستند. توجه داشته باشید که بالا بردن چگالی $\pi (.)$ به توان $1/T$ با $T>1$ شبیه گرما دادن به فلز، اثر یکنواخت کردن توزیع را دارد. در چنین توزیعی پیمودن بین قله‌ها (که با دره‌ها از هم جدا شده‌اند) راحت‌تر توزیع اصلی است. پس از هر تکرار تعویض حالتی بین دو زنجیره انتخاب شده تصادفی از طریق گام متروپلیس-نوع پیشنهاد شده‌است. اگر$\theta ^{(j)}$ حالت فعلی در زنجیره$j$ و $j=1,2,...,m$. تعویض بین حالات $i$ و $j$ زنجیر با احتمال زیر پذیرفته می‌شود:

$\alpha ={\frac {\pi _{i}(\theta ^{(j)})\pi _{j}(\theta ^{(i)})}{\pi _{i}(\theta ^{(i)})\pi _{j}(\theta ^{(j)})}}\$

در پایان اجرا، تنها خروجی زنجیره سرد استفاده می‌شود و خروجی‌های زنجیره گرم دور انداخته می‌شوند. به صورت اکتشافی، زنجیرهٔ گرم قله‌های محلی را راحت ملاقات خواهد کرد، و تعویض حالات بین زنجیرها به زنجیره سرد این اجازه را می‌دهد که گاهی اوقات از دره‌ها پرش کند که منجر به خروجی بهتر می‌شود. هرچند اگر$\pi _{i}(\theta )/\pi _{j}(\theta )$ ناپایدار باشد، تعویض پیشنهاد شده به ندرت پذیرفته می‌شود. به همین دلیل از چندین زنجیره مختلف استفاده می‌شود که تنها تفاوتش افزایش بودن آن است.

نقطه ضعف آشکار این الگوریتم این است که $m$ زنجیره اجرا می‌شود و تنها یک زنجیره برای استنباط استفاده می‌شود. به همین دلیل $(MC)^{3}$ به صورت ایده‌آل برای پیاده‌سازی روی ماشین‌های موازی مناسب است، از آن جایی که هر زنجیر در کل نیازمند همان مقدار یکسان محاسبه در هر تکرار است.

الگوریتم محلی لارگت و سیمون

الگوریتم‌های محلی مزیت محاسباتی نسبت به روش‌های پیشین ارائه می‌دهند و نشان می‌دهد که رویکرد بیزی قادر به ارزیابی عدم قطعیت محاسبات عملیاتی در درختان بزرگتر است. الگوریتم محلی بهبودیافته الگوریتم عمومی ارائه شده توسط مائو، نیوتن و لارگت(1999) است که در آن طول تمام شاخه‌ها در هر سیکل در حال تغییر است. الگوریتم محلی با انتخاب تصادفی یک شاخه درونی درخت، درخت را تغییر می‌دهد. گره‌های انتهایی این شاخه، هر کدام متصل به دو شاخهٔ دیگر متصل می‌شوند. هر کدام از این جفت‌ها به صورت تصادفی انتخاب می‌شود. تصور کنید که این سه یال انتخاب شده را گرفته‌اید و همانند طناب رخت از راست به چپ کشیده‌اید، که جهت کشیدن هم تصادفی انتخاب شده باشد (چپ/راست). دو نقطه انتهایی اولین شاخه انتخاب شده، زیر درخت معلق همانند تکه‌ای از لباس آویزان به طناب خواهد داشت. الگوریتم با تکثیر کردن سه شاخه انتخاب شده به مقدار تصادفی رایج، بسته به جمع شدن یا کشیده شدن رشته ادامه خواهد یافت. در نهایت زیر درخت معلق سمت چپ از دو زیر درخت معلق، قطع خواهد شد و به رشته، در مکانی که به صورت توزیع یکنواخت انتخاب خواهد شد وصل می‌شود. این درخت، درخت کاندید خواهد بود که.

فرض کنید با انتخاب شاخه داخلی با طول$t_{8}$ که $A$ و $B$ از گونه‌های دیگر جدا می‌کند، شروع کنیم. همچنین فرض کنید که ما (به صورت تصادفی) شاخه‌های با طول$t_{1}$ و $t_{9}$ را از هر طرف انتخاب کرده‌ایم و ما این شاخه‌ها را جهت یابی کرده‌ایم. فرض کنید که $m=t_{1}+t_{8}+t_{9}$طول رشته فعلی باشد. طول جدید را به این صورت تعیین می‌کنیم $m^{*}=m\exp(\lambda (U_{1}-0.5))$که در آن $U_{1}$ متغیر تصادفی یکنواخت در بازه $(0,1)$ می‌باشد. سپس برای الگوریتم محلی احتمال پذیرش به این صورت محاسبه می‌شود:

${\frac {h(y)}{h(x)}}\times {\frac {{m^{\star }}^{3}}{m^{3}}}\$

ارزیابی همگرایی

به منظور تخمین طول یک شاخه از یک درخت ۲-تاکسون تحت مدل Jukes-Cantor, که در آن $n_{1}$ مکان تغییرناپذیر و $n_{2}$ مکان تغییرپذیر باشد. فرض می‌کنیم که توزیع اولیع نمایی با پارامتر $\lambda$ باشد. تابع چگالی $p(t)=\lambda e^{-\lambda t}$. احتمالات ممکن مکان الگوها عبارتند از:

$1/4\left(1/4+3/4e^{-4/3t}\right)\$

برای مکان تغییرناپذیر و

$1/4\left(1/4-1/4e^{-4/3t}\right)\$

بنابراین توزیع پسین نرمال نشده:

$h(t)=\left(1/4\right)^{n_{1}+n_{2}}\left(1/4+3/4{e^{-4/3t}}^{n_{1}}\right)\$

یا متناوباً

$h(t)=\left(1/4-1/4{e^{-4/3t}}^{n_{2}}\right)(\lambda e^{-\lambda t})\$

آپدیت کردن طول شاخه با انتخاب مقدار جدید به صورت یکنواخت در تصادفی از یک پنجره نیمه عرض$w$ که مقدار فعلی مرکزش می‌باشد:

$t^{\star }=|t+U|\$

که در آن $U$در بازه $w$ و $-w$. احتمال پذیرش:

$h(t^{\star })/h(t)\$

مثال: $n_{1}=70$و $n_{1}=30$. ما نتایج را برای دو مقدار$w$،$w=0.1$ و $w=0.5$. در هر حالت با طول اولیه$5$ و دفعات تکرار آپدیت طول$2000$ بار.

بیشینه صرفه جویی و حداکثر درست نمایی

روابط فیلوژنتیک ببر، مقادیر خود راه انداز، در شاخه‌ها نشان داده شده‌اند.

مثالی از جذب شاخه طولانی. شاخه‌های بلندتر (A & C) بیشتر از شاخه‌های دیگر مرتبط به نظر می‌رسند.

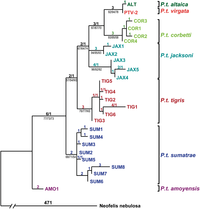
روش‌های زیادی برای بازسازی درختان فیلوژنتیک وجود دارند، هر کدام مزایا و معایب خود را دارد و پاسخ دقیقی برای این سؤال وجود ندارد: "بهترین روش کدام است؟". بیشینه صرفه جویی(MP) و حداکثر درست نمایی (ML) در روش‌های مرسومی هستند که برای تخمین فیلوژنی مورد استفاده قرار می‌گیرند. هر دو روش همانند روش‌های بیزی، از اطلاعات کاراکترها هم به‌طور مستقیم استفاده می‌کنند.

بیشینه صرفه‌جویی یکی (یا بیشتر) درخت بهینه را براساس ماتریس فاصله کاراکترها برای گروه خاصی از تاکسون و این نیازمند مدل تکاملی تغییر نیست. MP ساده‌ترین توضیح برای یک مجموعه داده می‌دهد، بازسازی یک درخت فیلوژنتیک که تا حد ممکن تغییرات کمی را در سراسر توالی داشته باشد، و این درخت کمترین تعداد مراحل تکاملی برای توضیح رابطه بین تاکسون‌ها را نشان می‌دهد. حمایت از شاخه‌های درخت توسط درصد بوت استرپ نمایش داده می‌شود. به همین دلیل سادگی آن است که به‌طور گسترده‌ای از آن استفاده شده‌است، انتقاداتی بر MP وارد شده‌است و توسط روش‌های حداکثر درست نمایی و بیزی به پس زمینه رانده شده‌است. MP ارائه مشکلات و محدودیت‌هایی را ارائه می‌کند. Joseph Felsenstein در سال (۱۹۷۸) نشان داد که MP ممکن است از نظر آماری ناسازگار باشد به این معنی که با داشتن داده‌های بیشتر و بیشتر (به عنوان مثال طول توالی) انباشته شده باشد، ممکن است نتایج به درخت نادرست همگرا شود و منجر به جذب شاخه طولانی - یک پدیده فیلوژنتیکی است که در آن تاکسون‌های با شاخه‌های بلند (تغییرات حالت کاراکتر متعدد)، مایل به این هستند که بیشتر از آن چیزی که در واقعیت هستند، در فیلوژنی ارتباط نزدیکتر داشته باشند - شود.

مثل بیشینه صرفه جویی، حداکثر درست نمایی، درختان دیگری را ارزیابی می‌کند. ضمناً احتمال اینکه هر درخت داده‌های داده شده را براساس مدل تکامل توصیف کند، در نظر می‌گیرد. در این روش درخت با بالاترین احتمال توصیف داده‌ها، انتخاب خواهد شد. به عبارت دیگر مقایسه‌ای بین درختان مختلف انجام می‌دهد، بر اساس اینکه چقدر هر درخت داده‌های مشاهده شده را پیش‌بینی می‌کنند. معرفی یک مدل تکامل در تحلیل ML، مزیتی نسبت به روش MP ارائه می‌کند: احتمال تعویض نوکلئوتید و نرخ این تعویض‌ها در نظر می‌گیرد، روابط فیلوژنتیک تاکسون را در قالب واقعی تر نشان می‌دهد. یک نکته مهم این روش، طول شاخه می‌باشد که تیغ اوکام آن را نادیده می‌گیرد، تغییرات در طول شاخه‌های بلندتر نسبت به رشته‌های کوتاهتر با احتمال بیشتر رخ می‌دهد. این رویکرد ممکن است جذب شاخه طولانی را نادیده بگیرد و سازگاری بیشتری از ML نسبت به MP توضیح دهد. اگر چه از دیدگاه تئوری توسط بسیاری به عنوان بهترین روش برای استنباط فیلوژنی در نظر گرفته شده، ML محاسبات سنگینی دارد و اکتشاف تمام درختان (تعداد بسیار زیاد درختان) تقریباً غیرممکن است. استنباط بیزی همچنین شامل یک مدل تکاملی است و از مزایای اصلی آن بر روش‌های MP و ML این است که از نظر محاسباتی کارآمد تر از روش‌های مرسوم می‌باشد، ضمناً می‌تواند منبع عدم قطعیت را تعیین نماید و قادر به این است که مدل‌های پیچیده تکامل را نیز لحاظ نماید.

مشکلات و مجادلات

• مقادیر بوت استرپ در مقابل احتمالات پسین. مشاهده شده که مقادیر پشتیبانی بوت استرپ، محاسبه شده تحت parsimony یا حداکثر درست نمایی، متمایل به پایین‌تر بودن از احتمالات پسین به دست آمده استنباط بیزی هستند. این واقعیت منجر به تعدادی از سوالات می‌شود: آیا احتمالات پسین منجر به اطمینان بیش از حد در نتایج خواهد شد؟ آیا مقادیر بوت استرپ پایدارتر از احتمالات پسین هستند؟
• جنجال استفاده از احتمالات پیشین. استفاده از احتمالات پیشین برای تحلیل بیزی، توسط بسیاری به عنوان یک مزیت شناخته شده‌است، که یک فرضیه با دیدگاه واقع بینانه تر از جهان واقعی ارائه می‌کند. با این حال برخی از زیست شناسان در مورد موضوعیت احتمال بیزی پسین پس از ترکیب با احتمالات پیشین بحث می‌کنند.
• انتخاب مدل. نتایج حاصل از تحلیل بیزی فیلوژنی به‌طور مستقیم مرتبط با مدل تکاملی انتخاب شده هستند، بنابراین مهم است که مدلی انتخاب شود که مناسب با داده‌های مشاهده باشد، در غیر این صورت استنتاج در فیلوژنی مستعد خطا خواهد بود. بسیاری از دانشمندان سوالاتی در مورد تفسیر استنباط بیزی دارند، زمانی که مدل ناشناخته یا نادرست باشد. برای مثال، یک مدل بیش از حد ساده شده ممکن است احتمالات پسین بالاتری بدهد یا مدل تکاملی ساده با عدم قطعیت کمتر از مقادیر بوت استرپ مرتبط هستند.

نرم‌افزار MRBAYES

MrBayes یک نرم‌افزار رایگان است که استنباط بیزی در فیلوژنی را انجام می‌دهد. این نرم‌افزار توسط John P. Huelsenbeck و Frederik Ronquist در سال ۲۰۰۱ نوشته شده‌است. با افزایش محبوبیت روش‌های بیزی، MrBayes نرم‌افزار منتخب بسیاری از متخصصین فیلوژنتیک مولکولی شد. این نرم‌افزار برای سیستم عامل‌های مکینتاش، ویندوز و یونیکس عرضه شده‌است و واسط خط فرمان دارد. این برنامه از الگوریتم استاندارد MCMC و الگوریتم MCMCMC استفاده می‌کند. MrBayes ماتریس‌های هم تراز یابی توالی (DNA یا اسیدهای آمینه) را از NEXUS format استاندارد می‌خواند.

MrBayes با استفاده از MCMC احتمالات پسین درختان را تقریب می‌زند. کاربر می‌تواند مفروضات مدل جایگزینی، احتمالات پیشین و جزئیات تحلیل MCMCMV را تغییر بدهد. همچنین اجازه حذف و اضافه کردن تاکسون و کاراکترها را به کاربر می‌دهد. این برنامه از استانداردترین مدل جایگزینی DNA، 4x4 یا مدل تعویضی استقاده می‌کند. با این فرض که تغییرات در سراسر نوکلئوتید با احتمال برابر رخ می‌دهد. همچنین تعداد 20x20 مدل جایگزینی اسید آمینه و مدل‌های کدون جایگزینی DNA را پیاده‌سازی کرده‌است. این نرم‌افزار روش‌های مختلف برای ساده‌سازی فرض نرخ جایگزینی یکسان در سراسر مکان‌های نوکلئوتید ارائه می‌دهد. MrBayes همچنین می‌تواند تطبیق عدم اطمینان حالات اجدادی به درخت فیلوژنتیک و پارامترهای مدل را استنباط کند.

MrBayes 3 نسخه کاملاً بازسازی شده تجدید سازمان یافته نسخه اصلی MrBayes می‌باشد. جدیدترین مورد این نسخه، توانایی این نرم‌افزار به تطبیق ناهمگونی از مجموعه داده است. این چارچوب جدید به کاربر اجازه می‌دهد تا مدل‌ها را ترکیب کند و از مزایای کارایی الگوریتم تحلیل بیزی MCMC در هنگام برخورد با نوع داده‌های مختلف استفاده کند (به عنوان مثال پروتئین، نوکلئوتید و ریخت‌شناسی (زیست‌شناسی)). این نرم‌افزار به صورت پیش فرض از الگوریتم MCMCMC استفاده می‌کند.

MrBayes 3.2 نسخه جدید MrBayes منتشر شده در سال ۲۰۱۲ می‌باشد. این نسخه جدید به کاربران اجازه می‌دهد تحلیل‌های چندگانه را به صورت موازی اجرا کنند. همچنین محاسبات سریعتر درست نمایی را فراهم کرده‌است و می‌توان این محاسبات را به GPU محول کرد. نسخه ۳٫۲ خروجی گسترده‌تری سازگار با FigTree و دیگر نرم‌افزارهای مشاهده درخت‌ها فراهم کرده‌است.

لیست نرم‌افزارهای فیلوژنتیک

این جدول شامل برخی از رایج‌ترین نرم‌افزارهای فیلوژنتیک استفاده شده برای درک استنباط فیلوژنی در چارچوب بیزی، می‌باشد. برخی از آن‌ها به‌طور انحصاری از روش‌های بیزی استفاده نمی‌کنند.

نام	توضیحات	روش	نویسنده	لینک وب سایت
نوعی حیوان گورکن پلت فرم گردش کار	گردش کار پلت فرم اختصاص داده شده به فیلوژنتیک و کلی بیوانفورماتیک تجزیه و تحلیل	استنتاج از درختان فیلوژنتیک با استفاده از فاصله‌های حداکثر احتمال Maximum Parsimonyهای بیزی و روش‌های مربوط به گردش	E. خداوند M. Leclercq A. Boc, A. B. دیللو و V. Makarenkov	https://web.archive.org/web/20161024081942/http://www.bioinfo.uqam.ca/armadillo/.
بالی-Phy	همزمان bayesian از تراز و تاریخ نژادی جانور یا گیاه	Bayesian تراز و همچنین درخت جستجو	M. A. Suchard, B. D. Redelings	http://www.bali-phy.org
BATWING	تحلیل بیزی از درختان با داخلی گره نسل	Bayesian جمعیتی تاریخچه جمعیت انشعابات	I. J. Wilson, D. Weale D. ریزش مو	http://www.maths.abdn.ac.uk/ijw
Bayes Phylogenies	Bayesian از درختان با استفاده از زنجیره مارکوف مونت کارلو روش	Bayesian, چند، مدل، مدل مخلوط (auto-پارتیشن‌بندی)	M. Pagel A. مید	http://www.evolution.rdg.ac.uk/BayesPhy.html
PhyloBayes / PhyloBayes MPI	بیزی زنجیره‌ای مارکوف مونت کارلو (MCMC) نمونه فیلوژنتیک برای بازسازی.	ناپارامتری روش‌های مدل‌سازی در میان سایت تنوع در نوکلئوتید یا آمینو اسید گرایش.	N. Lartillot N. Rodrigue D. Stubbs, J. غنی تر	https://web.archive.org/web/20181218053945/http://www.phylobayes.org/
جانور	بیزی تکاملی تجزیه و تحلیل نمونه برداری از درختان	Bayesian, آرام، مولکولی، ساعت جمعیتی تاریخچه	A. J. Drummond, A. Rambaut & M. A. Suchard	http://beast.bio.ed.ac.uk
BUCKy	بیزی تطابق ژن درختان	بیزی تطابق با استفاده از اصلاح حریص اجماع unrooted کوارتت	C. Ané, B. Larget D. A. Baum, S. D. Smith, A. Rokas و B. Larget, S. K. Kotha, C. N. دیویی، C. Ané	http://www.stat.wisc.edu/~ane/bucky/
Geneious (MrBayes پلاگین)	Geneious ابزارهای پژوهش ژنوم و پروتئوم را فراهم می‌کند	همسایه-پیوستن UPGMA با MrBayes پلاگین PHYML پلاگین RAxML پلاگین FastTree پلاگین GARLi پلاگین PAUP** ** پلاگین	A. J. Drummond,M. Suchard V. Lefort et al.	http://www.geneious.com
TOPALi	استنتاج فیلوژنتیک	فیلوژنتیک مدل، انتخاب، بیز، تجزیه و تحلیل و حداکثر احتمال درخت فیلوژنتیک برآورد تشخیص سایت‌های تحت مثبت انتخاب و نوترکیبی انفصال محل تجزیه و تحلیل	I. Milne, D. Lindner, et al.	http://www.topali.org

کاربردها

متخصصین فیلوژنتیک مولکولی به‌طور گسترده از استنباط بیزی استفاده می‌کنند. برخی از این خدمات عبارتند از:

ماده تاریخ به دست آمده از تحلیل ساعت مولکولی با استفاده از BEAST. نمودار دایره‌ای در هر گره توزیع اجدادی ممکن استنتاج شده از تحلیل باینری بیزی MCMC را نشان می‌دهد.

• استنباط فیلوژنی‌ها.
• استنباط و ارزیابی عدم اطمینان فیلوژنی ها
• استنباط اجدادی حالت تکامل ویژگی اجدادی.
• استنتاج نواحی اجدادی.
• تحلیل زمانی مولکولی.
• مدل پویای تنوع و انقراض گونه‌ها.
• بررسی الگوهای پراکندگی پاتوژن‌ها.

پیوند به بیرون

• MrBayes official website
• BEAST official website