گستران

دو گستران (قرمز) یک سهمی

در ریاضیات، گُستَران یا اینولوت (انگلیسی: Involute) نوع خاصی از منحنی است که به شکل یا منحنی دیگری وابسته است. گستران یک منحنی، مکان هندسی یک نقطه روی یک قطعه نخ کشیده است که نخ یا از روی منحنی باز می‌شود یا دور آن پیچیده می‌شود.

گسترندهٔ یک منحنی گستران، منحنی اصلی است.

این مفهوم توسط خانواده منحنی‌های غلتان تعمیم می‌یابد؛ یعنی گستران‌های یک منحنی، غلتان‌های (رولت‌های) منحنی هستند که توسط یک خط مستقیم ایجاد می‌شوند.

مفاهیم گستران و گسترندهٔ (evolute) یک منحنی توسط کریستیان هویگنس در اثر خود با عنوان ساعت آونگی (۱۶۷۳) معرفی شد، جایی که او نشان داد که گستران یک چرخ‌زاد هنوز یک چرخ‌زاد است، بنابراین روشی برای ساخت چرخ‌زاد ارائه داد که دارای ویژگی مفید این است که دوره آن مستقل از دامنه نوسان است.

گستران یک منحنی پارامتری

فرض کنید ${\vec {c}}(t),\;t\in [t_{1},t_{2}]$ یک منحنی در صفحه باشد که انحنا آن هیچ جا صفر نیست و $a\in (t_{1},t_{2})$، سپس منحنی با نمایش پارامتری

${\vec {C}}_{a}(t)={\vec {c}}(t)-{\frac {{\vec {c}}'(t)}{|{\vec {c}}'(t)|}}\;\int _{a}^{t}|{\vec {c}}'(w)|\;dw$

یک گستران از منحنی داده شده است.

اثبات رشته به عنوان یک مماس به منحنی ${\vec {c}}(t)$ عمل می‌کند. طول آن با مقداری برابر با طول قوس طی شده هنگام پیچیدن یا باز شدن تغییر می‌کند. طول قوس منحنی طی شده در بازه $[a,t]$ توسط $\int _{a}^{t}|{\vec {c}}'(w)|\;dw$ داده می‌شود، که $a$ نقطه شروع است که از آنجا طول قوس اندازه‌گیری می‌شود. از آنجایی که بردار مماس نشان دهنده رشته کشیده در اینجا است، بردار رشته را به صورت ${\frac {{\vec {c}}'(t)}{|{\vec {c}}'(t)|}}\;\int _{a}^{t}|{\vec {c}}'(w)|\;dw$ به دست می‌آوریم. بردار مربوط به نقطه انتهایی رشته (${\vec {C}}_{a}(t)$) را می‌توان به راحتی با استفاده از جمع بردار محاسبه کرد و به دست می‌آید ${\vec {C}}_{a}(t)={\vec {c}}(t)-{\frac {{\vec {c}}'(t)}{|{\vec {c}}'(t)|}}\;\int _{a}^{t}|{\vec {c}}'(w)|\;dw$

با اضافه کردن یک عدد دلخواه اما ثابت $l_{0}$ به انتگرال ${\Bigl (}\int _{a}^{t}|{\vec {c}}'(w)|\;dw{\Bigr )}$، یک گستران متناظر با یک نخ که به اندازه $l_{0}$ افزایش یافته است (مانند یک توپ نخ که قبل از باز شدن مقداری نخ از آن آویزان است) به دست می‌آید. از این رو، گستران را می‌توان با ثابت $a$ و/یا اضافه کردن یک عدد به انتگرال تغییر داد (به گستران‌های یک سهمی نیمه‌مکعبی مراجعه کنید).

اگر ${\vec {c}}(t)=(x(t),y(t))^{T}$ باشد، به دست می‌آید:

${\begin{aligned}X(t)&=x(t)-{\frac {x'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(w)^{2}+y'(w)^{2}}}\,dw\\Y(t)&=y(t)-{\frac {y'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(w)^{2}+y'(w)^{2}}}\,dw\;.\end{aligned}}$

ویژگی‌های گستران‌ها

گستران: ویژگی‌ها. زوایای نشان داده شده ۹۰ درجه هستند.

برای به دست آوردن ویژگی‌های یک منحنی منظم، بهتر است فرض کنیم طول قوس $s$ پارامتر منحنی داده شده باشد، که منجر به ساده‌سازی‌های زیر می‌شود: $\;|{\vec {c}}'(s)|=1\;$ and $\;{\vec {c}}''(s)=\kappa (s){\vec {n}}(s)\;$، که $\kappa$ انحنا و ${\vec {n}}$ بردار نرمال واحد است. برای گستران به دست می‌آید:

${\vec {C}}_{a}(s)={\vec {c}}(s)-{\vec {c}}'(s)(s-a)\$ and

${\vec {C}}_{a}'(s)=-{\vec {c}}''(s)(s-a)=-\kappa (s){\vec {n}}(s)(s-a)\;$

و عبارت:

• در نقطه ${\vec {C}}_{a}(a)$ گستران منظم نیست (زیرا $|{\vec {C}}_{a}'(a)|=0$)،

و از $\;{\vec {C}}_{a}'(s)\cdot {\vec {c}}'(s)=0\;$ نتیجه می‌شود:

• نرمال گستران در نقطه ${\vec {C}}_{a}(s)$، مماس منحنی داده شده در نقطه ${\vec {c}}(s)$ است.
• گستران‌ها منحنی موازی هستند، به دلیل ${\vec {C}}_{a}(s)={\vec {C}}_{0}(s)+a{\vec {c}}'(s)$ و این واقعیت که ${\vec {c}}'(s)$ نرمال واحد در ${\vec {C}}_{0}(s)$ است.

خانواده گستران‌ها و خانواده مماس‌های منحنی اصلی یک دستگاه مختصات متعامد را تشکیل می‌دهند. در نتیجه، می‌توان گستران‌ها را به صورت گرافیکی ساخت. ابتدا، خانواده خطوط مماس را رسم کنید. سپس، یک گستران را می‌توان با همیشه عمود ماندن بر خط مماس عبوری از نقطه ساخت.

تیزه‌ها

این بخش بر اساس این منبع است.

به‌طور کلی دو نوع تیزه (کاسپ) در گستران‌ها وجود دارد. نوع اول در نقطه‌ای است که گستران منحنی را لمس می‌کند. این یک تیزه از مرتبه ۳/۲ است. نوع دوم در نقطه‌ای است که منحنی دارای نقطه عطف است. این یک تیزه از مرتبه ۵/۲ است.

این را می‌توان با ساختن یک نگاشت $f:\mathbb {R} ^{2}\to \mathbb {R} ^{3}$ که توسط $$(s,t)\mapsto (x(s)+t\cos(\theta ),y(s)+t\sin(\theta ),t)$$ تعریف می‌شود، به صورت بصری مشاهده کرد، که در آن $(x(s),y(s))$ پارامتری طول قوس منحنی است و $\theta$ زاویه شیب منحنی در نقطه $(x(s),y(s))$ است. این صفحه ۲ بعدی را به یک سطح در فضای ۳ بعدی نگاشت می‌کند. به عنوان مثال، این دایره را به هذلولی‌گون نگاشت می‌کند.

با این نگاشت، گستران‌ها در یک فرایند سه مرحله‌ای به دست می‌آیند: نگاشت $\mathbb {R}$ به $\mathbb {R} ^{2}$، سپس به سطح در $\mathbb {R} ^{3}$، سپس با حذف محور z آن را به $\mathbb {R} ^{2}$ تصویر کنید: $$s\mapsto (s,l-s)\mapsto f(s,l-s)\mapsto (f(s,l-s)_{x},f(s,l-s)_{y})$$ که در آن $l$ هر ثابت حقیقی است.

از آنجایی که نگاشت $s\mapsto f(s,l-s)$ در همه $s\in \mathbb {R}$ دارای مشتق غیرصفر است، تیزه‌های گستران فقط در جایی می‌توانند رخ دهند که مشتق $s\mapsto f(s,l-s)$ عمودی باشد (موازی با محور z)، که فقط در جایی می‌تواند رخ دهد که سطح در $\mathbb {R} ^{3}$ دارای یک صفحه مماس عمودی باشد.

به‌طور کلی، سطح در دو حالت دارای صفحات مماس عمودی است: جایی که سطح منحنی را لمس می‌کند و جایی که منحنی دارای یک نقطه عطف است.

تیزه از مرتبه ۳/۲

برای نوع اول، می‌توان با گستران یک دایره، با معادله زیر شروع کرد: $${\begin{aligned}X(t)&=r(\cos t+(t-a)\sin t)\\Y(t)&=r(\sin t-(t-a)\cos t)\end{aligned}}$$ سپس $a=0$ را قرار داده و برای $t$ کوچک بسط دهید تا به دست آید: $${\begin{aligned}X(t)&=r+rt^{2}/2+O(t^{4})\\Y(t)&=rt^{3}/3+O(t^{5})\end{aligned}}$$ بنابراین منحنی مرتبه ۳/۲ $Y^{2}-{\frac {8}{9r}}(X-r)^{3}+O(Y^{8/3})=0$، یک سهمی نیمه‌مکعبی، به دست می‌آید.

تیزه از مرتبه ۵/۲

مماس‌ها و گستران‌های منحنی مکعبی $y=x^{3}$. تیزه‌های مرتبه ۳/۲ روی منحنی مکعبی هستند، در حالی که تیزه‌های مرتبه ۵/۲ روی محور x (خط مماس در نقطه عطف) هستند.

برای نوع دوم، منحنی $y=x^{3}$ را در نظر بگیرید. قوس از $x=0$ تا $x=s$ طول $\int _{0}^{s}{\sqrt {1+(3t^{2})^{2}}}dt=s+{\frac {9}{10}}s^{5}-{\frac {9}{8}}s^{9}+O(s^{13})$ دارد و مماس در $x=s$ زاویه $\theta =\arctan(3s^{2})$ دارد؛ بنابراین، گستران شروع شده از $x=0$ در فاصله $L$ دارای فرمول پارامتری زیر است: $${\begin{cases}x(s)=s+(L-s-{\frac {9}{10}}s^{5}+\cdots )\cos \theta \\y(s)=s^{3}+(L-s-{\frac {9}{10}}s^{5}+\cdots )\sin \theta \end{cases}}$$ آن را تا مرتبه $s^{5}$ بسط دهید، به دست می‌آید: $${\begin{cases}x(s)=L-{\frac {9}{2}}Ls^{4}+({\frac {9}{2}}L-{\frac {9}{10}})s^{5}+O(s^{6})\\y(s)=3Ls^{2}-2s^{3}+O(s^{6})\end{cases}}$$ که یک تیزه از مرتبه ۵/۲ است. به صراحت، می‌توان برای بسط چند جمله‌ای ارضا شده توسط $x,y$ حل کرد: $$\left(x-L+{\frac {y^{2}}{2L}}\right)^{2}-\left({\frac {9}{2}}L+{\frac {51}{10}}\right)^{2}\left({\frac {y}{3L}}\right)^{5}+O(s^{11})=0$$ یا $$x=L-{\frac {y^{2}}{2L}}\pm \left({\frac {9}{2}}L+{\frac {51}{10}}\right)\left({\frac {y}{3L}}\right)^{2.5}+O(y^{2.75}),\quad \quad y\geq 0$$ که به وضوح شکل تیزه را نشان می‌دهد.

با قرار دادن $L=0$، گستران عبوری از مبدأ را به دست می‌آوریم. این مورد خاص است زیرا شامل هیچ تیزه‌ای نیست. با بسط سری، معادله پارامتری آن به صورت زیر است: $${\begin{cases}x(s)={\frac {18}{5}}s^{5}-{\frac {126}{5}}s^{9}+O(s^{13})\\y(s)=-2s^{3}+{\frac {54}{5}}s^{7}-{\frac {318}{5}}s^{11}+O(s^{15})\end{cases}}$$ یا $x=-{\frac {18}{5\cdot 2^{1/3}}}y^{5/3}+O(y^{3})$

مثال‌ها

گستران‌های یک دایره

گستران‌های یک دایره

برای یک دایره با نمایش پارامتری $(r\cos(t),r\sin(t))$، داریم:

${\vec {c}}'(t)=(-r\sin t,r\cos t)$.

بنابراین $|{\vec {c}}'(t)|=r$، و طول مسیر $r(t-a)$ است.

با ارزیابی معادله گستران داده شده در بالا، به دست می‌آید:

${\begin{aligned}X(t)&=r(\cos(t+a)+t\sin(t+a))\\Y(t)&=r(\sin(t+a)-t\cos(t+a))\end{aligned}}$

برای معادله پارامتری گستران دایره.

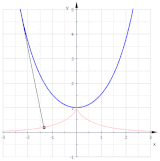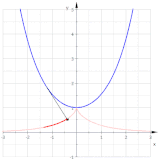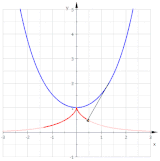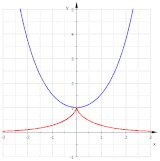
جمله $a$ اختیاری است؛ این برای تنظیم مکان شروع منحنی روی دایره استفاده می‌شود. شکل گستران‌ها را برای $a=-0.5$ (سبز)، $a=0$ (قرمز)، $a=0.5$ (بنفش) و $a=1$ (آبی روشن) نشان می‌دهد. گستران‌ها شبیه مارپیچ ارشمیدس هستند، اما در واقع اینطور نیستند.

طول قوس برای $a=0$ و $0\leq t\leq t_{2}$ از گستران برابر است با:

$L={\frac {r}{2}}t_{2}^{2}.$

گستران‌های یک سهمی نیمه‌مکعبی (آبی). فقط منحنی قرمز یک سهمی است. توجه کنید که چگونه گستران‌ها و مماس‌ها یک دستگاه مختصات متعامد را تشکیل می‌دهند. این یک واقعیت کلی است.

گستران‌های یک سهمی نیمه‌مکعبی

معادله پارامتری ${\vec {c}}(t)=({\tfrac {t^{3}}{3}},{\tfrac {t^{2}}{2}})$ یک سهمی نیمه‌مکعبی را توصیف می‌کند. از ${\vec {c}}'(t)=(t^{2},t)$ به دست می‌آید $|{\vec {c}}'(t)|=t{\sqrt {t^{2}+1}}$ و $\int _{0}^{t}w{\sqrt {w^{2}+1}}\,dw={\frac {1}{3}}{\sqrt {t^{2}+1}}^{3}-{\frac {1}{3}}$. گسترش نخ به اندازه $l_{0}={1 \over 3}$ محاسبات بعدی را بسیار ساده می‌کند و به دست می‌آید:

${\begin{aligned}X(t)&=-{\frac {t}{3}}\\Y(t)&={\frac {t^{2}}{6}}-{\frac {1}{3}}.\end{aligned}}$

حذف t منجر به $Y={\frac {3}{2}}X^{2}-{\frac {1}{3}},$ می‌شود که نشان می‌دهد این گستران یک سهمی است.

سایر گستران‌ها بنابراین منحنی‌های موازی یک سهمی هستند و سهمی نیستند، زیرا منحنی‌هایی از درجه شش هستند.

گستران قرمز یک زنجیره‌وار (آبی) یک کشاننده است.

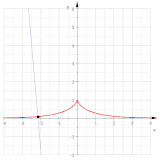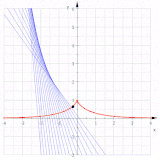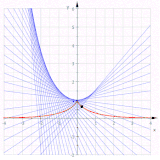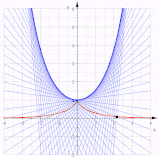
گستران‌های یک زنجیره‌وار

برای زنجیره‌وار $(t,\cosh t)$، بردار مماس ${\vec {c}}'(t)=(1,\sinh t)$ است و، به عنوان $1+\sinh ^{2}t=\cosh ^{2}t,$ طول آن $|{\vec {c}}'(t)|=\cosh t$ است؛ بنابراین طول قوس از نقطه (۰, ۱) برابر است با $\textstyle \int _{0}^{t}\cosh w\,dw=\sinh t.$

از این رو گستران شروع شده از (۰, ۱) توسط

$(t-\tanh t,1/\cosh t),$

پارامتری می‌شود و بنابراین یک کشاننده (تراکتریکس) است.

سایر گستران‌ها کشاننده نیستند، زیرا منحنی‌های موازی یک کشاننده هستند.

گستران‌های یک چرخ‌زاد

گستران‌های یک چرخ‌زاد (آبی): فقط منحنی قرمز یک چرخ‌زاد دیگر است

نمایش پارامتری ${\vec {c}}(t)=(t-\sin t,1-\cos t)$ یک چرخ‌زاد را توصیف می‌کند. از ${\vec {c}}'(t)=(1-\cos t,\sin t)$، (پس از استفاده از برخی فرمول‌های مثلثاتی) به دست می‌آید:

$|{\vec {c}}'(t)|=2\sin {\frac {t}{2}},$

و

$\int _{\pi }^{t}2\sin {\frac {w}{2}}\,dw=-4\cos {\frac {t}{2}}.$

از این رو معادلات گستران متناظر عبارتند از:

$X(t)=t+\sin t,$

$Y(t)=3+\cos t,$

که چرخ‌زاد قرمز منتقل شده در نمودار را توصیف می‌کنند. از این رو

• گستران‌های چرخ‌زاد $(t-\sin t,1-\cos t)$ منحنی‌های موازی چرخ‌زاد زیر هستند:

$(t+\sin t,3+\cos t).$

(منحنی‌های موازی یک چرخ‌زاد، چرخ‌زاد نیستند)

گستران و گسترنده

گسترنده یک منحنی داده شده $c_{0}$ شامل مراکز انحنای $c_{0}$ است. بین گستران‌ها و گسترنده‌ها عبارت زیر برقرار است:

یک منحنی، گسترندهٔ هر یک از گستران‌های آن است.

گستران و گسترنده

• 
  کشاننده (قرمز) به عنوان گستران یک زنجیره‌وار
• 
  گسترنده یک کشاننده یک زنجیره‌وار است

کاربرد

رایج‌ترین پروفیل‌های دندانه‌های چرخ‌دنده مدرن، گستران‌های یک دایره هستند. در یک دستگاه چرخ‌دنده گستران، دندانه‌های دو چرخ‌دنده درگیر در یک نقطه لحظه‌ای واحد که در امتداد یک خط مستقیم حرکت می‌کند، تماس پیدا می‌کنند. نیروهایی که دندانه‌های در تماس بر یکدیگر وارد می‌کنند نیز از این خط پیروی می‌کنند و بر دندانه‌ها عمود هستند. سامانه چرخ‌دنده گستران که این شرایط را حفظ می‌کند، از قانون اساسی چرخ‌دنده‌ها پیروی می‌کند: نسبت سرعت‌های زاویه‌ای بین دو چرخ‌دنده باید در طول حرکت ثابت بماند.

با دندانه‌هایی با شکل‌های دیگر، سرعت‌ها و نیروها با درگیر شدن دندانه‌های متوالی بالا و پایین می‌روند و منجر به لرزش، سر و صدا و سایش بیش از حد می‌شوند. به همین دلیل، تقریباً تمام سامانه‌های چرخ‌دنده مسطح مدرن یا گستران یا سیستم مرتبط چرخ‌دنده چرخ‌زاد هستند.

سازوکار یک کمپرسور غلتشی

گستران یک دایره همچنین یک شکل مهم در کمپرسور است، زیرا یک کمپرسور غلتشی می‌تواند بر اساس این شکل ساخته شود. کمپرسورهای اسکرال صدای کمتری نسبت به کمپرسورهای معمولی تولید می‌کنند و ثابت شده است که بازده مکانیکی بالایی دارند.

راکتور ایزوتوپی با شار بالا از عناصر سوختی به شکل گستران استفاده می‌کند، زیرا این عناصر اجازه می‌دهند یک کانال با عرض ثابت بین آنها برای خنک‌کننده وجود داشته باشد.

جستارهای وابسته

• منحنی محاطی
• چرخ‌دنده گستران

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Involute». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۱۹ ژوئیه ۲۰۲۴.