درگ (فیزیک)

زمانی که یک شیء در گاز یا مایع حرکت می‌کند نیرویی در خلاف جهت حرکت شی به آن وارد می‌شود. یک کره در جریان استوکس در عدد رینولدز پایین نشان داده شده است.

در دینامیک سیالات، درگ یا پسار (به انگلیسی: drag) (گاهی اوقات مقاومت سیال نامیده می‌شود) نیرویی است که برخلاف حرکت نسبی هر جسمی که نسبت به سیال اطراف حرکت می‌کند، عمل می‌کند. این می‌تواند بین دو لایه (یا سطح) سیال یا بین سطح سیال و جامد وجود داشته باشد.

برخلاف سایر نیروهای مقاومتی، مانند اصطکاک خشک، که تقریباً مستقل از سرعت هستند، نیروی پسا به سرعت بستگی دارد. نیروی کشش متناسب با سرعت برای جریان کم سرعت و سرعت مربع برای جریان با سرعت بالا است که در آن تمایز بین سرعت کم و زیاد با عدد رینولدز اندازه‌گیری می‌شود.

نیروهای کششی همیشه تمایل به کاهش سرعت سیال نسبت به جسم جامد در مسیر سیال دارند.

مثال‌ها

نمونه‌هایی از درگ شامل مؤلفه‌ای از نیروی خالص آیرودینامیکی یا هیدرودینامیکی است که برخلاف جهت حرکت یک جسم جامد مانند اتومبیل‌ها (ضریب کشش خودرو)، هواپیماها و بدنه قایق‌ها عمل می‌کند. یا در همان جهت حرکت جغرافیایی جامد عمل می‌کند، مانند بادبان‌های متصل به قایق بادبانی، یا در جهت‌های متوسط روی بادبان بسته به نقاط بادبان یا در مورد کشش چسبناک سیال در یک لوله یا نیروی کشش روی لوله بی حرکت یاسرعت سیال را نسبت به لوله کاهش می‌دهد. در فیزیک ورزش، نیروی درگ برای توضیح حرکت توپ‌ها، نیزه‌ها، تیرها و فریزبی‌ها و عملکرد دوندگان و شناگران ضروری است.

انواع نیروی Drag

شکل و جریان	پسار فشاری	پسار اصطکاکی
	۰٪	۱۰۰٪
	~۱۰٪	~۹۰٪
	~۹۰٪	~۱۰٪
	۱۰۰٪	۰٪

انواع درگ به‌طور کلی به دسته‌های زیر تقسیم می‌شوند:

• حالت درگ یا فشار به اندازه و شکل جسم بستگی دارد.
• درگ اصطکاک سطحی یا درگ گرانروی، اصطکاک بین سیال و سطحی که ممکن است بیرون جسم یا داخل باشد مانند سوراخ لوله بستگی دارد.

اثر جریان‌سازی بر نسبت‌های نسبی اصطکاک سطحی و حالت درگ برای دو بخش مختلف جسم، یک ایرفویل (airfoil)، که بدنه‌ای استریم‌لاین (streamlined) است، و یک سیلندر، که بدنه بلوف (bluff body) است، که در جدول روبه رو نشان داده شده است. همچنین یک صفحه تخت که نشان دهنده تأثیر جهت‌گیری بر نسبت نسبی اصطکاک سطحی و اختلاف فشار بین جلو و عقب است. یک جسم به عنوان بلوف (یا بلانت) شناخته می‌شود اگر منبع درگ تحت تسلط نیروهای فشار باشد و همچنین درگ تحت تسلط نیروهای گرانروی باشد، ساده می‌شود. وسایل نقلیه بدنه بلوفی هستند. برای هواپیما، درگ فشاری و اصطکاکی نیروی مزاحم است. درگ مزاحم غالباً بر حسب یک "معادل مساحت درگ مزاحم " فرضی (تا جایی که هیچ کشش لبه ای وجود ندارد)" بیان می‌شود که مساحت صفحه صاف عمود بر جریان است. برای مقایسه درگ هواپیماهای مختلف استفاده می‌شود. به عنوان مثال، "داگلاس دی سی-۳ "مساحت مزاحم معادل ۲۳٫۷ فوت مربع دارد و "مک دانل داگلاس دی سی-۹" با ۳۰ سال پیشرفت در طراحی هواپیما، مساحتی معادل ۲۰٫۶ فوت مربع را داراست، اگرچه پنج برابر بیشتر، مسافر را حمل می‌کرد.

• درگ ناشی از بالابر با بال یا بدنه بالابر در هوانوردی و با بدنه‌های نیمه برنامه‌ریز یا برنامه‌ریز برای کشتی‌ها ظاهر می‌شود.
• درگ موجی (آیرودینامیک) به دلیل وجود امواج ضربه ای ایجاد می‌شود و اولین بار در سرعت‌های هواپیمای مادون صوت زمانی که سرعت‌های جریان محلی مافوق صوت می‌شود ظاهر می‌شود. درگ موجی هواپیمای نمونه اولیه «کنکورد» مافوق صوت با اعمال قانون منطقه که بدنه عقب هواپیمای تولیدی را ۳٫۷۳ متر افزایش داد، در ۲ ماخ به میزان ۱٫۸ درصد کاهش یافت.
• مقاومت موجی (هیدرودینامیک کشتی) یا درگ موجی زمانی اتفاق می‌افتد که یک جسم جامد در امتداد مرز سیال حرکت می‌کند و امواج سطحی ایجاد می‌کند.
• درگ دم-قایق در هواپیما به دلیله اینکه زاویه ای است به بدنه عقب، یا نازل موتور، یا به قطر اگزوز موتور محدود می‌کند.

معادله درگ

Drag coefficient C_d for a sphere as a function of Reynolds number Re, as obtained from laboratory experiments. The dark line is for a sphere with a smooth surface, while the lighter line is for the case of a rough surface.

درگ به خواص سیال و اندازه، شکل و سرعت جسم بستگی دارد. یکی از راه‌های بیان این موضوع با استفاده از معادله درگ است: $$F_{D}\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{D}\,A$$ که

• $F_{D}$ نیرو درگ
• $\rho$ چگالی سیال
• $v$ سرعت جسم در سیال
• $A$ سطح مقطع
• $C_{D}$ ضریب درگ
  ضریب درگ به شکل جسم و عدد رینولدز بستگی دارد.$$R_{e}={\frac {vD}{\nu }}={\frac {\rho vD}{\mu }},$$که
• D قطر مشخصه
• برای یک مقطع مستطیلی شکل در جهت حرکت$D_{e}=1.30\cdot {\frac {(a\cdot b)^{0.625}}{(a+b)^{0.25}}}$که در آن a و b لبه‌های مستطیل هستند.
• ${\nu }$ ویسکوزیته سینماتیک

در رینولدز و ضریب درگه پایین به‌طور مجانبی متناسب است با معکوس رینولدز به این معنی که کشش به‌طور خطی با سرعت متناسب است، یعنی نیروی پسا روی یک کره کوچک که در یک سیال چسبناک حرکت می‌کند توسط قانون استوکس به دست می‌آید:

$$F_{\rm {d}}=3\pi \mu Dv$$

در رینولدز و ضریب درگه بالا کم و بیش ثابت است و کشیدن به عنوان مربع سرعت تغییر می‌کند. نمودار سمت راست نشان می‌دهد که چگونه ضریب درگ متفاوت است با رینولدز برای مثال یک کره از آنجایی که توان لازم برای غلبه بر نیروی درگ حاصل ضرب نیرو در سرعت است، توان لازم برای غلبه بر درگ به صورت مربع سرعت در اعداد رینولدز پایین و مکعب سرعت در اعداد بالا متفاوت خواهد بود.

می‌توان نشان داد که نیروی پسا را می‌توان به عنوان تابعی از یک عدد بی بعد بیان کرد که از نظر ابعادی با عدد بژان یکسان است. در نتیجه، نیروی پسا و ضریب درگ می‌تواند تابعی از عدد بژان باشد. در واقع از بیان نیروی پسا بدست آمده است:

$$F_{\rm {d}}=\Delta _{p}A_{w}={\frac {1}{2}}C_{D}A_{f}{\frac {\nu \mu }{l^{2}}}Re_{L}^{2}$$

و در نتیجه اجازه بیان ضریب درگ را می‌دهد به عنوان تابعی از عدد بژان و نسبت بین سطح مرطوب$A_{w}$ و مساحت جلو $A_{f}$

$$C_{D}=2{\frac {A_{w}}{A_{f}}}{\frac {Be}{Re_{L}^{2}}}$$

که $Re_{L}$ عدد رینولدز مربوط به طول مسیر سیال L است.

درگ در سرعت‌های بالا

همان‌طور که گفته شد، معادله درگ با ضریب درگ ثابت، نیرویی را که جسمی با سرعت نسبتاً زیادی در یک سیال در حال حرکت است (یعنی عدد رینولدز بالا، Re>~۱۰۰۰) تجربه می‌کند. به این درگ درجه دوم نیز گفته می‌شود. این معادله به لرد ریلی نسبت داده می‌شود، که در ابتدا از L2 به جای A استفاده کرد (L مقداری طول است).

$F_{D}\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{D}\,A$

مشتق این معادله در معادله درگ مشتق ارائه شده است.

ناحیه مرجع A غالباً برآمدگی اشیاء (ناحیه جلویی) - در صفحه ای عمود بر جهت حرکت - است، به عنوان مثال برای اجسام با شکل ساده، مانند یک کره، این سطح مقطع است. گاهی اوقات یک جسم مرکب از قسمت‌های مختلف است که هر یک دارای مناطق مرجع متفاوتی است، در این صورت باید ضریب درگ مربوط به هر یک از آن نواحی مختلف تعیین شود.

در مورد یک بال، مناطق مرجع یکسان هستند و نیروی پسا به همان نسبت نسبت ضریب پسا به ضریب بالابر است؛ بنابراین، مرجع برای یک بال اغلب ناحیه بالابر ("ناحیه بال") به جای ناحیه جلویی است.

برای یک جسم با سطح صاف، و نقاط جداسازی غیر ثابت - مانند یک کره یا استوانه دایره‌ای - ضریب درگ ممکن است با عدد رینولدز Re، حتی تا مقادیر بسیار بالا (Re از مرتبه ۱۰۷) متفاوت باشد. برای یک جسم با نقاط جداسازی ثابت به خوبی تعریف شده، مانند یک دیسک دایره‌ای که صفحه آن در جهت جریان عادی است، ضریب پسا برای Re > 3500 ثابت است. علاوه بر این، ضریب پسا C_d، به‌طور کلی، تابعی از جهت‌گیری جریان نسبت به جسم است (به غیر از اجسام متقارن مانند یک کره).

قدرت

با این فرض که سیال نسبت به سیستم مرجع فعلی مورد استفاده حرکت نمی‌کند، قدرت مورد نیاز برای غلبه بر کشش آیرودینامیکی به صورت زیر داده می‌شود:

$$P_{d}=\mathbf {F} _{d}\cdot \mathbf {v} ={\tfrac {1}{2}}\rho v^{3}AC_{d}$$

قدرت مورد نیاز برای راندن یک جسم از درون یک سیال با مکعب سرعت افزایش می‌یابد. خودرویی که در یک بزرگراه با سرعت ۸۰ کیلومتر در ساعت حرکت می‌کند، ممکن است برای غلبه بر کشش آیرودینامیک تنها به ۱۰ اسب بخار (۷٫۵ کیلووات) نیاز داشته باشد، اما همان خودرو با سرعت ۱۰۰ مایل در ساعت (۱۶۰ کیلومتر در ساعت) به ۸۰ اسب بخار (۶۰ کیلووات) نیاز دارد. با دو برابر شدن سرعت، درگ (نیرو) در هر فرمول چهار برابر می‌شود. اعمال ۴ برابر نیرو در یک فاصله ثابت، ۴ برابر بیشتر کار تولید می‌کند. با سرعت دو برابر کار (که منجر به جابجایی در یک فاصله ثابت می‌شود) دو برابر سریعتر انجام می‌شود. از آنجایی که توان، میزان انجام کار است، ۴ برابر کار انجام شده در نیمی از زمان نیاز به ۸ برابر توان دارد.

هنگامی که سیال نسبت به سیستم مرجع در حال حرکت است (مثلاً اتومبیلی که به سمت باد مخالف حرکت می‌کند) قدرت مورد نیاز برای غلبه بر کشش آیرودینامیکی توسط: $$P_{d}=\mathbf {F} _{d}\cdot \mathbf {v_{o}} ={\tfrac {1}{2}}C_{d}A\rho (v_{w}+v_{o})^{2}v_{o}$$

که $v_{w}$ سرعت باد و $v_{o}$ سرعت جسم (هر دو نسبت به زمین) است.

سرعت یک جسم در حال سقوط

سرعت به عنوان تابعی از زمان برای جسمی که در یک محیط غیر متراکم سقوط می‌کند و با سرعت نسبی صفر v = ۰ در زمان t = ۰ آزاد می‌شود، تقریباً با تابعی شامل یک مماس هذلولی (tanh) داده می‌شود:

$$v(t)={\sqrt {\frac {2mg}{\rho AC_{d}}}}\tanh \left(t{\sqrt {\frac {g\rho C_{d}A}{2m}}}\right).\,$$

مماس هذلولی دارای مقدار حدی یک است، برای زمان t بزرگ. به عبارت دیگر، سرعت به‌طور مجانبی به حداکثر مقداری به نام سرعت نهایی v_t نزدیک می‌شود:

$$v_{t}={\sqrt {\frac {2mg}{\rho AC_{d}}}}.\,$$

برای جسمی که با سرعت نسبی سقوط می‌کند و رها می‌شود v = v_i در زمان t = ۰، با v_i <v_t، بر حسب تابع مماس هذلولی نیز تعریف می‌شود:

$$v(t)=v_{t}\tanh \left(t{\frac {g}{v_{t}}}+\operatorname {arctanh} \left({\frac {v_{i}}{v_{t}}}\right)\right).\,$$

برای v_i > v_t، تابع سرعت بر حسب تابع کاتانژانس هذلولی تعریف می‌شود:

$$v(t)=v_{t}\coth \left(t{\frac {g}{v_{t}}}+\coth ^{-1}\left({\frac {v_{i}}{v_{t}}}\right)\right).\,$$

کوتانژانت هذلولی نیز مقدار حدی یک دارد، برای زمان t زیاد. سرعت به‌طور مجانبی به سرعت پایانی v_t میل می‌کند، دقیقاً از بالای v_t.

برای v_i = v_t، سرعت ثابت است:

$$v(t)=v_{t}.$$

در واقع، این توابع با حل معادله دیفرانسیل زیر تعریف می‌شوند:

$$g-{\frac {\rho AC_{d}}{2m}}v^{2}={\frac {dv}{dt}}.\,$$

یا به‌طور کلی تر (جایی که F(v) نیروهایی هستند که فراتر از کشش بر جسم وارد می‌شوند):

$${\frac {1}{m}}\sum F(v)-{\frac {\rho AC_{d}}{2m}}v^{2}={\frac {dv}{dt}}.\,$$

برای یک جسم سیب زمینی شکل با قطر متوسط d و چگالی ρ_obj، سرعت نهایی حدود

$$v_{t}={\sqrt {gd{\frac {\rho _{obj}}{\rho }}}}.\,$$

برای اجسام با چگالی آب مانند (قطرات باران، تگرگ، اشیاء زنده - پستانداران، پرندگان، حشرات، و غیره) که در هوا در نزدیکی سطح زمین در سطح دریا سقوط می‌کنند، سرعت نهایی تقریباً برابر است با

$$v_{t}=90{\sqrt {d}},\,$$

سرعت پایانی برای موجودات بزرگتر بالاتر است و بنابراین به‌طور بالقوه کشنده تر است. موجودی مانند موش که با سرعت نهایی خود سقوط می‌کند، احتمال بیشتری دارد که از برخورد با زمین جان سالم به در ببرد تا انسانی که با سرعت نهایی خود سقوط کند. حیوان کوچکی مانند جیرجیرک که با سرعت نهایی خود برخورد می‌کند احتمالاً آسیبی نمی‌بیند. این، همراه با نسبت نسبی سطح مقطع اندام به توده بدن (که معمولاً به عنوان قانون مکعب مربع نامیده می‌شود)، توضیح می‌دهد که چرا حیوانات بسیار کوچک می‌توانند از ارتفاع زیاد بیفتند و آسیبی به آنها نرسد.

آیرودینامیک

در آیرودینامیک، کشش آیرودینامیک (همچنین به عنوان مقاومت هوا شناخته می‌شود) نیروی کششی سیالی است که بر هر جسم جامد متحرکی در جهت جریان آزاد هوا عمل می‌کند. از دیدگاه بدن (رویکرد میدان نزدیک)، پسا ناشی از نیروهای ناشی از توزیع فشار بر روی سطح بدن است که نماد آن است.

D_pr, و نیروهای ناشی از اصطکاک پوست که در نتیجه ویسکوزیته است، نشان داده شده است D_f روش دیگر، محاسبه شده از دیدگاه میدان جریان (رویکرد میدان دور)، نیروی پسا از سه پدیده طبیعی ناشی می‌شود: امواج ضربه، ورتکس و ویسکوزیته.

بررسی اجمالی

توزیع فشاری که بر روی سطح بدن اعمال می‌شود، نیروهای عادی را بر بدن وارد می‌کند. این نیروها را می‌توان جمع کرد و جزء آن نیرویی که در پایین دست عمل می‌کند نیروی پسا را نشان می‌دهد. D_pr، به دلیل توزیع فشار بر روی بدن. ماهیت این نیروهای عادی اثرات موج ضربه، اثرات تولید سیستم گردابی و مکانیسم‌های چسبناک بیدار را ترکیب می‌کند. ویسکوزیته سیال تأثیر عمده ای بر درگ دارد. در غیاب ویسکوزیته، نیروهای فشاری که برای عقب‌انداختن خودرو عمل می‌کنند، توسط نیروی فشاری در عقب‌تر که خودرو را به سمت جلو هل می‌دهد، لغو می‌شود. این بازیابی فشار نامیده می‌شود و نتیجه این است که درگ صفر است؛ یعنی کاری که بدن بر روی جریان هوا انجام می‌دهد برگشت‌پذیر است و بازیابی می‌شود زیرا هیچ اثر اصطکاکی برای تبدیل انرژی جریان به گرما وجود ندارد. بازیابی فشار حتی در مورد جریان ویسکوز نیز عمل می‌کند. با این حال، ویسکوزیته منجر به کشش فشار می‌شود و جزء غالب درگ در مورد وسایل نقلیه با مناطق جریان مجزا است که در آن بازیابی فشار نسبتاً بی اثر است. نیروی کشش اصطکاک، که یک نیروی مماس بر روی سطح هواپیما است، به‌طور عمده به پیکربندی لایه مرزی و ویسکوزیته بستگی دارد. کشش اصطکاک خالص، D_f، به عنوان پیش‌بینی پایین دست نیروهای ویسکوز بر روی سطح بدن محاسبه می‌شود. مجموع درگ اصطکاک و پسا فشار (شکل) کشش چسبناک نامیده می‌شود. این جزء درگ به دلیل ویسکوزیته است. در منظر ترمودینامیکی، اثرات چسبناک پدیده‌های برگشت‌ناپذیر را نشان می‌دهند و بنابراین، آنتروپی ایجاد می‌کنند. کشش ویسکوز محاسبه شده D_v از تغییرات آنتروپی برای پیش‌بینی دقیق نیروی پسا استفاده کنید. هنگامی که هواپیما بالابر ایجاد می‌کند، یکی دیگر از اجزای درگ ایجاد می‌شود. کشش القایی، نمادین D_i، به دلیل تغییر در توزیع فشار به دلیل سیستم گردابی دنباله دار است که تولید آسانسور را همراهی می‌کند. یک دیدگاه جایگزین در مورد لیفت و درگ از در نظر گرفتن تغییر تکانه جریان هوا به دست می‌آید. بال جریان هوا را قطع می‌کند و جریان را مجبور می‌کند تا به سمت پایین حرکت کند. این منجر به یک نیروی برابر و مخالف به سمت بالا بر روی بال می‌شود که نیروی بالابر است. تغییر تکانه جریان هوا به سمت پایین منجر به کاهش تکانه عقب جریان می‌شود که نتیجه نیرویی است که به جلو بر جریان هوا وارد می‌شود و توسط بال به جریان هوا اعمال می‌شود. یک نیروی مساوی اما متضاد بر روی بال به سمت عقب اعمال می‌کند که نیروی پسا القایی است. یکی دیگر از اجزای درگ، یعنی کشش موج، D_w، ناشی از امواج ضربه ای در سرعت پرواز فراصوت و مافوق صوت است. امواج ضربه ای باعث ایجاد تغییراتی در لایه مرزی و توزیع فشار در سطح بدن می‌شود.

به‌طور خلاصه، سه راه برای دسته‌بندی درگ وجود دارد.

• کشش فشار و کشش اصطکاک
• کشیدن نمایه و کشیدن القایی
• Vortex drag, wave drag و wake drag

تاریخچه

این ایده که جسم متحرکی که از هوا یا سیال دیگری عبور می‌کند با مقاومت مواجه می‌شود از زمان ارسطو شناخته شده بود. به گفته مروین اوگرمن، آرچیبالد ریث لو آن را «کشیدن» نامیده است. مقاله لوئی چارلز برگه در سال ۱۹۲۲ تلاش‌هایی را برای کاهش کشش با ساده‌سازی آغاز کرد. Breguet با طراحی چندین هواپیمای رکوردشکن در دهه‌های ۱۹۲۰ و ۱۹۳۰ ایده‌های خود را عملی کرد. تئوری لایه مرزی لودویگ پراندتل در دهه ۱۹۲۰ انگیزه ای برای به حداقل رساندن اصطکاک پوست ایجاد کرد. درخواست اصلی دیگر برای ساده‌سازی توسط سر ملویل جونز انجام شد که مفاهیم نظری را برای نشان دادن اهمیت ساده‌سازی در طراحی هواپیما ارائه کرد. در سال ۱۹۲۹ مقاله او با عنوان «هواپیمای ساده» که به انجمن سلطنتی هوانوردی ارائه شد بسیار مهم بود. او یک هواپیمای ایده‌آل را پیشنهاد کرد که دارای حداقل نیروی کششی باشد که منجر به مفاهیم یک هواپیمای تک هواپیمای «تمیز» و زیرشاخه جمع شونده شد. جنبه ای از مقاله جونز که بیشتر طراحان آن زمان را شوکه کرد، طرح قدرت اسب مورد نیاز در مقابل سرعت، برای یک هواپیمای واقعی و ایده‌آل بود. با نگاه کردن به یک نقطه داده برای یک هواپیمای معین و برون یابی آن به صورت افقی به منحنی ایده‌آل، افزایش سرعت برای همان توان قابل مشاهده است. هنگامی که جونز سخنرانی خود را به پایان رساند، یکی از حضار نتایج را به همان اندازه اهمیت چرخه کارنو در ترمودینامیک توصیف کرد.

درگ ناشی از لیفت و درگ مزاحم

درگ ناشی از لیفت (که به آن درگ القایی نیز گفته می‌شود) درگ است که در نتیجه ایجاد بالابر روی بدنه بالابر سه بعدی مانند بال یا پروانه هواپیما اتفاق می‌افتد. درگ القایی اصولاً از دو جزء تشکیل شده است: درگ به دلیل ایجاد گرداب‌های دنباله دار (کشش گردابی). و وجود درگ ویسکوز اضافی (کشش چسبناک ناشی از بالابر) که در زمانی که لیفت صفر است وجود ندارد. گرداب‌های دنباله دار در میدان جریان، که در پی یک جسم بالابر وجود دارند، از اختلاط متلاطم هوا از بالا و پایین بدن ناشی می‌شوند که در نتیجه ایجاد بالابر در جهت‌های کمی متفاوت جریان می‌یابد. با ثابت ماندن سایر پارامترها، با افزایش لیفت تولید شده توسط بدنه، کشش ناشی از لیفت نیز افزایش می‌یابد. این به این معنی است که با افزایش زاویه حمله بال (تا حداکثر به نام زاویه توقف)، ضریب لیفت نیز افزایش می‌یابد و درگ ناشی از لیفت نیز افزایش می‌یابد. در شروع استال، لیفت به‌طور ناگهانی کاهش می‌یابد، همان‌طور که دراگ ناشی از لیفت کاهش می‌یابد، اما کشش فشار چسبناک، جزء درگ انگل، به دلیل تشکیل جریان ناپیوسته آشفته در پشت بدنه افزایش می‌یابد.

درگ مزاحم

کشش مزاحم یا درگ پروفایل، درگ ناشی از حرکت یک جسم جامد در یک سیال است. درگ مزاحم از اجزای متعددی از جمله کشش فشار ویسکوز (کشش فرم) و درگ ناشی از زبری سطح (درگ اصطکاک سطح) تشکیل شده است. علاوه بر این، وجود اجسام متعدد در مجاورت نسبی ممکن است به اصطلاح باعث درگ تداخلی شود که گاهی اوقات به عنوان جزئی از درگ مزاحم توصیف می‌شود. در هوانوردی، درگ القایی در سرعت‌های پایین‌تر بیشتر می‌شود، زیرا برای حفظ بالابر به زاویه حمله بالا نیاز است و درگ بیشتری ایجاد می‌کند. با این حال، با افزایش سرعت، زاویه حمله را می‌توان کاهش داد و درگ القایی کاهش می‌یابد. با این حال، کشش انگلی افزایش می‌یابد زیرا سیال با سرعت بیشتری در اطراف اجسام بیرون زده جریان دارد و اصطکاک یا درگ را افزایش می‌دهد. در سرعت‌های حتی بالاتر (ترانسونیک)، درگ موج وارد تصویر می‌شود. هر یک از این اشکال درگ به تناسب سایر اشکال بر اساس سرعت تغییر می‌کند؛ بنابراین، منحنی درگ کلی ترکیبی، حداقل را در برخی از سرعت‌های هوایی نشان می‌دهد - هواپیمایی که با این سرعت پرواز می‌کند، بازده بهینه یا نزدیک به آن خواهد بود. خلبانان از این سرعت برای به حداکثر رساندن استقامت (حداقل مصرف سوخت) یا به حداکثر رساندن برد سر خوردن در صورت خرابی موتور استفاده خواهند کرد.

منحنی قدرت در هوانوردی

برهمکنش درگ مزاحم و القایی در مقابل سرعت هوا را می‌توان به عنوان یک منحنی مشخصه ترسیم کرد که در اینجا نشان داده شده است. در هوانوردی، این اغلب به عنوان منحنی قدرت نامیده می‌شود و برای خلبانان مهم است، زیرا نشان می‌دهد که در زیر یک سرعت هوایی خاص،

The power curve: parasitic drag and lift-induced drag vs. airspeed

مقالهٔ اصلی: Drag curve

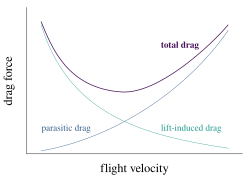
حفظ سرعت هوایی به‌طور غیر مستقیم به نیروی رانش بیشتر با کاهش سرعت نیاز دارد، نه کمتر. عواقب "پشت منحنی" بودن در پرواز مهم است و به عنوان بخشی از آموزش خلبانی آموزش داده می‌شود. در سرعت‌های هوایی مادون صوت که شکل "U" این منحنی قابل توجه است، کشش موج هنوز به یک عامل تبدیل نشده است و بنابراین در منحنی نشان داده نمی‌شود.

کشش موج در جریان فراصوت و مافوق صوت

درگ موجی (که به آن کشش تراکم‌پذیری نیز می‌گویند) به درگی گفته می‌شود که وقتی جسمی در یک سیال تراکم‌پذیر حرکت می‌کند و با سرعت‌هایی نزدیک به سرعت صوت در آن

Qualitative variation in Cd factor with Mach number for aircraft

مقالهٔ اصلی: Wave drag

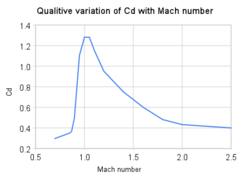
سیال ایجاد می‌شود. در آیرودینامیک، کشش موج از چندین مؤلفه بسته به رژیم سرعت پرواز تشکیل شده است. در پرواز فرا صوت (اعداد ماخ بزرگتر از حدود ۰٫۸ و کمتر از حدود ۱٫۴)، کشش موج نتیجه تشکیل امواج ضربه ای در سیال است که هنگام ایجاد نواحی محلی جریان مافوق صوت (عدد ماخ بیشتر از ۱٫۰) ایجاد می‌شود. در عمل، جریان مافوق صوت در اجسامی که بسیار کمتر از سرعت صوت حرکت می‌کنند، اتفاق می‌افتد، زیرا سرعت محلی هوا با افزایش سرعت روی بدن به سرعت‌های بالاتر از ۱٫۰ ماخ افزایش می‌یابد. با این حال، جریان مافوق صوت کامل روی خودرو تا زمانی که ۱٫۰ ماخ نگذشته باشد، ایجاد نخواهد شد. هواپیماهایی که با سرعت فراصوتی پرواز می‌کنند اغلب در مسیر عادی عملیات متحمل کشش موج می‌شوند. در پرواز فراصوتی، کشش موج معمولاً به عنوان کشش تراکم پذیری فراصونی شناخته می‌شود. با افزایش سرعت پرواز به سمت ۱٫۰ ماخ، کشش تراکم پذیری فراصونی به‌طور قابل توجهی افزایش می‌یابد و بر دیگر اشکال پسا در این سرعت‌ها غالب می‌شود. در پرواز مافوق صوت (اعداد ماخ بزرگتر از ۱٫۰)، کشش موج نتیجه امواج ضربه ای است که در سیال وجود دارد و به بدن متصل می‌شود، معمولاً امواج ضربه ای مورب در لبه‌های جلویی و انتهایی بدن ایجاد می‌شود. در جریان‌های بسیار مافوق صوت، یا در اجسامی با زاویه چرخش به اندازه کافی بزرگ، امواج ضربه‌ای ناپیوسته یا امواج کمانی شکل می‌گیرند. علاوه بر این، نواحی محلی جریان فراصوتی در پشت موج ضربه‌ای اولیه ممکن است در سرعت‌های مافوق صوت پایین‌تر رخ دهد و می‌تواند منجر به ایجاد امواج ضربه‌ای اضافی و کوچک‌تر روی سطوح دیگر اجسام بالابر شود، مشابه آنچه در جریان‌های فراصوت یافت می‌شود. در رژیم‌های جریان مافوق صوت، کشش موج معمولاً به دو جزء، کشش موج وابسته به لیفت مافوق صوت و کشش موج وابسته به حجم مافوق صوت تقسیم می‌شود. راه حل شکل بسته برای کشش موج حداقل یک جسم چرخشی با طول ثابت توسط Sears و Haack پیدا شد و به عنوان Sears-Haack Distribution شناخته می‌شود. به‌طور مشابه، برای یک حجم ثابت، شکل برای کشش حداقل موج، فون کارمان اوگیو است.

مفهوم نظری دوبال Busemann در هنگام کار با سرعت طراحی خود در معرض کشش موج نیست، اما در این شرایط قادر به ایجاد بالابر نیست.

پارادوکس دالامبر

در سال ۱۷۵۲ دالامبر ثابت کرد که جریان پتانسیل، نظریه جریان غیر لزج پیشرفته قرن هجدهم که متمایل به حل‌های ریاضی بود، منجر به پیش‌بینی کشش صفر شد. این در تضاد با شواهد تجربی بود و به پارادوکس d'Alembert معروف شد. در قرن نوزدهم معادلات ناویر-استوکس برای توصیف جریان ویسکوز توسط Saint-Venant, Navier و Stokes ایجاد شد. استوکس کشش به دور یک کره را با اعداد رینولدز بسیار پایین بدست آورد که نتیجه آن قانون استوکس نامیده می‌شود.

در حد اعداد رینولدز بالا، معادلات ناویر-استوکس به معادلات اویلر غیر لزج نزدیک می‌شوند، که راه‌حل‌های جریان پتانسیل در نظر گرفته شده توسط دالامبر راه‌حل‌هایی هستند. با این حال، تمام آزمایش‌ها در اعداد رینولدز بالا نشان دادند که کشش وجود دارد. تلاش برای ساخت راه‌حل‌های جریان پایدار غیر لزج برای معادلات اویلر، به غیر از راه‌حل‌های جریان بالقوه، به نتایج واقعی منجر نشد. مفهوم لایه‌های مرزی - که توسط پراندتل در سال ۱۹۰۴ ارائه شد، هم بر اساس تئوری و هم بر اساس آزمایش‌ها پایه‌گذاری شد - علل درگ در اعداد رینولدز بالا را توضیح داد. لایه مرزی لایه نازکی از سیال نزدیک به مرز جسم است، جایی که اثرات چسبناک حتی زمانی که ویسکوزیته بسیار کوچک است (یا به‌طور معادل عدد رینولدز بسیار بزرگ است) مهم باقی می‌ماند.

جستارهای وابسته

• ضریب پسار
• پسارگیر

منابع

• Currie, I. G. Fundamental Mechanics of Fluids, McGraw-Hill, Inc. , 1974. ISBN 0-07-014950-X
• Munson B.R. Fundamentals of Fluid Mechanics, John Wiley & Sons, Inc. , 2002. ISBN 0-471-44250-X