هفت تکه تانگرام

تانگرام (به چینی: 七巧板)، (به پینیین :qī qiǎo bǎn)، (به انگلیسی: Tangram)یک بازی با ۷ قطعهٔمسطح است که با در کنار هم گذاشتن آنها، شکلهای گوناگونی ساخته میشود. معمولاً طرح کلی شکل حاصل به فرد داده میشود و هدف بازی این است که او بتواند با چینش این قطعات، شکل مورد نظر را بسازد. گفته میشود که این بازی در چین و در دوره دودمان سونگ اختراع شده و در سدهٔ نوزدهم میلادی با کشتیهای تجاری به اروپا راه یافتهاست.[۱]
این بازی، یکی از محبوبترین بازیهای جورچین در جهان است.[۲][۳] یک روانشناس چینی، این بازی را اولین تست روانشناسی جهان دانسته، با این تفاوت که به جای آنالیز روانی برای سرگرمی مورد استفاده قرار میگرفتهاست.[۱]
ریشهٔ واژه[ویرایش]
به نظر میرسد که واژه تنگرام از به هم پیوستن واژه tan (برگرفته از دودمان تانگ) و واژه یونانی gramma (هممعنی گراف) پدید آمدهباشد.
تناقضات[ویرایش]
یک تناقض تنگرام هنگامی پدید میآید که دو شکلی که با همین هفت قطعه ساخته شدهاند چنین به نظر میرسد که مساحتهای متفاوتی را پوشش دادهاند و به نظر میرسد که یکی از آنها قطعهای اضافی دارد. (در حالیکه چنین نیست) یکی از تناقضات مشهور در تنگرام را هنری دودنی کشف کرد که مربوط به دو شکل یک راهب است که یکی از آنها پا دارد و دیگری ندارد. در حقیقت پای اضافه از جابجایی قطعات بدست آمدهاست و هیچ قطعهای در هیچیک از دو شکل اضافه یا کم نشدهاست. یکی دیگر از تناقضات معروف را سم لوید کشف کرده که با نام تناقض جام جادویی تنگرام، در کتاب هشت کتاب تان (The Eighth Book Of Tan) آمدهاست. (چاپشده به سال ۱۹۰۳ میلادی)
-
تناقض دو راهب. هر دو شکل شبیه به یکدیگرند ولی یکی از آنها پا دارد.
-
تناقض جام جادویی تنگرام. با هفت قطعهٔ استاندارد تنگرام، این سه شکل متفاوت ساخته شده که دو تا از آنها در درون خود قسمتهای خالی دارند. چگونگی ساختن هر یک از این سه طرح در پایین تصویر نشان داده شدهاست. (دقت کنید که شکل سمت چپ کوتاهتر از دوتای دیگر و شکل میانی پهنتر از آن دوتای دیگر است.)[۴]
-
تناقض مربع بریده. از کتاب لوید (۱۹۰۳ میلادی)
طرحها[ویرایش]
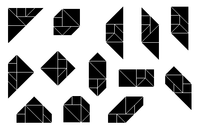
در کتابهایی که در سدهٔ نوزدهم دربارهٔتنگرام نوشته شد، بیش از ۶۵۰۰ شکل آورده شده که با تنگرام میتوان ساخت و تا امروز این تعداد در حال افزایش است؛ با این حال شمار اشکالی که میتوان با تنگرام ساخت پایانپذیراند. فو تراینگ وانگ و چوآن-چین ژیونگ در سال ۱۹۴۲ ثابت کردند که تنها ۱۹ شکل کوژ (یک چندضلعی که اگر قطری بین هر دو راس آن رسم کنیم از محیط آن بیرون نرود) را میتوان با قطعات تنگرام ساخت.[۵][۶]
قطعات[ویرایش]
قطعات به گونهای انتخاب شدهاند که با چینش آنها میتوان به یک مربع دست یافت. اگر هر ضلع این مربع را برابر یک واحد در نظر بگیریم داریم:
- دو مثلث قائمالزاویه بزرگ (طول وتر برابر یک واحد، طول دو ضلع دیگر برابر ، با مساحت یک چهارم واحد)
- یک مثلث قائمالزاویه متوسط (طول وتر برابر ، طول دو ضلع دیگر برابر یک دوم واحد، با مساحت یک هشتم واحد)
- دو مثلث قائمالزاویه کوچک (طول وتر برابر یک دوم واحد، طول دو ضلع دیگر برابر ، با مساحت یک شانزدهم واحد)
- یک مربع (با طول ضلع ، مساحت یک هشتم واحد)
- یک متوازیالأضلاع (با اضلاعی به طول یک دوم واحد و واحد، مساحت یک هشتم واحد)
پانویس[ویرایش]
- ↑ ۱٫۰ ۱٫۱ Jiannong Shi (2 February 2004). Robert J. Sternberg (ed.). International Handbook of Intelligence. Cambridge University Press. pp. 330–331. ISBN 978-0-521-00402-2.
- ↑ Slocum, Jerry (2001). The Tao of Tangram. Barnes & Noble. p. 9. ISBN 978-1-4351-0156-2.
- ↑ Forbrush, William Byron (1914). Manual of Play. Jacobs. p. 315. Retrieved 10/13/10.
{{cite book}}: Check date values in:|accessdate=(help) - ↑ «نسخه آرشیو شده». بایگانیشده از اصلی در ۲۸ ژانویه ۲۰۱۶. دریافتشده در ۱۶ سپتامبر ۲۰۱۴.
- ↑ Fu Traing Wang; Chuan-Chih Hsiung (November 1942). "A Theorem on the Tangram". The American Mathematical Monthly. 49 (9): 596–599. doi:10.2307/2303340. JSTOR 2303340.
- ↑ Read, Ronald C. (1965). Tangrams: 330 Puzzles. New York: Dover Publications. p. 53. ISBN 0-486-21483-4.
منابع[ویرایش]
- مشارکتکنندگان ویکیپدیا. «Tangram». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۵ شهریور ۱۳۹۳.


![تناقض جام جادویی تنگرام. با هفت قطعهٔ استاندارد تنگرام، این سه شکل متفاوت ساخته شده که دو تا از آنها در درون خود قسمتهای خالی دارند. چگونگی ساختن هر یک از این سه طرح در پایین تصویر نشان داده شدهاست. (دقت کنید که شکل سمت چپ کوتاهتر از دوتای دیگر و شکل میانی پهنتر از آن دوتای دیگر است.)[۴]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/f5/The_Magic_Dice_Cup_tangram_paradox.svg/120px-The_Magic_Dice_Cup_tangram_paradox.svg.png)


