الگوریتم جستجوی دودویی
این مقاله به دلیل یک مقدار نامرتب نیازمند تمیزکاری است. لطفاً تا جای امکان آنرا از نظر املا، انشا، چیدمان و درستی بهتر کنید، سپس این برچسب را بردارید. محتویات این مقاله ممکن است غیر قابل اعتماد و نادرست یا جانبدارانه باشد یا قوانین حقوق پدیدآورندگان را نقض کرده باشد. |
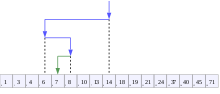 Visualization of the binary search algorithm where 7 is the target value | |
| رده | الگوریتم جستجو |
|---|---|
| ساختمان داده | آرایه (ساختار داده) |
| کارایی بدترین حالت | O(log n) |
| کارایی بهترین حالت | O(1) |
| کارایی متوسط | O(log n) |
| پیچیدگی فضایی | O(1) |
الگوریتم جستجوی دودویی (به انگلیسی: Binary Search) یا جستجوی دودویی خوارزمی، تکنیکی است برای یافتن یک مقدار عددی از میان مجموعهای از اعداد مرتب. این متد محدودهٔ جستجو را در هر مرحله به نصف کاهش میدهد، بنابراین هدف مورد نظر یا به زودی پیدا میشود یا مشخص میشود که مقدار مورد جستجو در فهرست وجود ندارد.
جستجوی دودویی فقط در آرایههای مرتب استفاده میشود. در این روش عنصر مورد نظر با خانه وسط آرایه مقایسه میشود اگر با این خانه برابر بود جستجو تمام میشود اگر عنصر مورد جستجو از خانه وسط بزرگتر بود جستجو در بخش بالایی آرایه و در غیر این صورت جستجو در بخش پایینی آرایه انجام میشود (فرض کردهایم آرایه به صورت صعودی مرتب شدهاست) این رویه تا یافتن عنصر مورد نظر یا بررسی کل خانههای آرایه ادامه مییابد.
جستجوی دودویی نمونهای از الگوریتمهای تقسیم و غلبه (به انگلیسی: Divide and conquer) میباشد.
مقدمه[ویرایش]
پیدا کردن اندیس یک عنصر خاص در یک لیست مرتب شده مفید است زیرا با استفاده از اندیس داده شده میتوان به سایر اطلاعات مربوط دست یافت.
فرض کنید داده ساختاری شامل مجموعهای از اطلاعات نام آدرس و شماره تلفن و غیرهاست و آرایه ای که نامها را دربردارد از ۱ تا N شمارهگذاری شدهاست، یک در خواست میتواند این باشد: شماره فردی به نام X چند است. برای پاسخ دادن به این سؤال آرایه مورد نظر باید جستجو شده و اندیس مربوط به نام داده شده در صورت وجود برگردانده شود، در این حالت شماره تلفن ذخیره شده در آرایه تلفنها در این اندیس، همان شماره فرد X است و به همین ترتیب برای آدرس و غیره نیز میتوان عمل کرد.
خواص درخت دودویی[ویرایش]
n تعداد گرهها در یک درخت دودویی کامل است و با استفاده از این فرمول میتوان آن را یافت (در آن h عمق درخت است) N تعداد گرهها در یک درخت دودویی کامل است حداقل برابر و حداکثر برابر (h عمق درخت است) L تعدادی از گرههای برگ در درخت دودویی کامل است و با استفاده از فرمول محاسبه میگردد.
N تعداد گرهها در یک درخت دودویی کامل نیز میتواند با استفاده فرمول محاسبه میشود. (L، تعدادی از گرههای برگ در درخت است)
تعدادی از لینکهای تهی (فرزندان غایب از گرهها) در یک درخت دودویی کامل از n گره تعداد از گرههای داخلی در یک درخت دودویی کامل از n گره (گرههای غیر برگ) . برای هر درخت غیر تهی با گرههای برگ و گرهها از درجه 2 .
اثبات:
N = تعداد کل گره B = تعداد شاخهها
- n0, n1, n2 برای نشان دادن تعداد گره بدون فرزند، تنها یک فرزند و دو فرزند بود
- B = n - 1 (از آنجا که تمام گرهها به جز گره ریشه از شاخه واحد)
- B = n1 + 2*n2
- n = n1+ 2*n2 + 1
- n = n0 + n1 + n2
- n1+ 2*n2 + 1 = n0 + n1 + n2 ==> n0 = n2 + 1
مثال[ویرایش]
بازیهای حدس شماره[ویرایش]
این بازیهای ساده با چیزی شبیه این شروع میشوند:" من عددی را بین ۴۰ و ۶۰ در نظر گرفتهام و تو آن را حدس میزنی و من با این پاسخها تو را راهنمایی میکنم: کمتر، بیشتر و بله!
فرض کنید تعداد اعداد ممکن برابر N است، بنابراین سؤال لازم است تا عدد مورد نظر پیدا شود چون هر سؤال فضای جستجو را نصف میکند.
حتی اگر محدودهٔ اعداد مورد نظر نا محدود باشد (یعنی توسط N محدود نشده باشد) باز هم میتوان با حداکثر مرحله (که K عدد انتخاب شدهاست) عدد مورد نظر را یافت. بدین ترتیب که با شروع از یک و دو برابر کردن آن در هر مرحله ابتدا مرز بالایی را پیدا نموده و سپس عدد خواسته شده را پیدا میکنیم. به عنوان مثال اگر عدد انتخاب شده ۱۱ باشد ما میتوانیم ترتیب پرسشهای زیر را برای پیدا کردن عدد دنبال کنیم: ۱ ← ۲ ← ۴ ← ۸ ← ۱۶ ← ۱۲ ← ۱۰ ← ۱۱.
هم چنین میتوان این تکنیک را گسترش داد تا شامل اعداد منفی نیز بشود، به عنوان مثال حدسهای زیر دنبال میشوند تا عدد ۱۳- پیدا شود: ۰ ← ۱- ← ۲- ← ۴- ← ۸- ← ۱۶- ← ۱۲- ← ۱۴- ← ۱۳-.
لیستهای کلمات[ویرایش]
انسانها معمولاً ترکیبی از جستجوی دودویی و الگوریتمهای جستجوی الحاقی را هنگام جستجوی دفترچه تلفن به کار میبرند. بعد از حدس اولیه ما از این حقیقت استفاده میکنیم که ورودیها مرتب اند و در نتیجه سریع تر به هدف میرسیم. مثلاً وقتی به دنبال «کریمی» میگردیم اگر «گنجی» و «قلی پور» پیدا شوند ما میتوانیم به صفحهای بین حدسهای قبلی مراجعه کنیم و اگر مثلاً «کمالی» را نشان میداد میدانیم که صفحهٔ مورد نظر جایی بین «قلی پور» و «کمالی» خواهد بود.
تابع[ویرایش]

برای این که وارد جزئیات تابع شویم باید قراردادهای رسمی تری را تعریف کنیم. ایده اولیه این است که داده ساختاری وجود دارد که به صورت آرایه A نمایش داده میشود، و المانهای آن به صورت A(1), A(2),…,A توصیف میشوند و به هر ترتیبی قابل دستیابیاند.
داده ساختاری شامل دادهٔ دیگری به نام Key میشود، آرایه به گونهای مرتب میشود که A(1).Key <= A(2).Key و ….
هدف این است که مقدار x داده شده و اندیس p پیدا شود بهطوریکه A(p).Key = x.
برای آغاز محدودهای که باید جستجو شود کل دادههایی است که با متغیرهای L و R مشخص میشود و این مرزها در هر بار تکرار الگوریتم کاهش مییابند.
پیادهسازی[ویرایش]
تکرار[ویرایش]
یکی از روش ها برای پیدا کردن عنصر مورد نظر x در یک آرایه بنام A روش تکرار است،که مراحل زیر را شامل می شود:
1.دو متغیر i و j به ترتیب مقادیر اولیه 0 و n-1 را می گیرند.(n طول آرایه مورد نظر است.)
2.تا زمانیکه است مراحل زیر را اجرا می کنیم:
2.1.متغیر k مقدار را که همان سقف است را می گیرد.
2.2.اگر باشد، j مقدار k-1 میگیرد.
2.3.اگر باشد، i مقدار k را میگیرد.
3.حال است،اگر بود، i را خروجی میدهیم در غیر این صورت خروجی نخواهیم داشت.
Niklaus Wirth الگوریتم تکرار را در پاسکال ارائه کردهاست:
i := 1;
j := N; {array size: var A: array [1..N] of integer}
repeat
k := (i + j) div 2;
if x> A[k] then
i := k + 1
else
j := k - 1;
until (A[k] = x) or (i> j);
بازگشتی[ویرایش]
پیادهسازی متداول این تابع توسط الگوریتم بازگشتی زیر میباشد:
BinarySearch(A[0..N-1], value, low, high) {
if (high <low)
return -1 // not found
mid = low + ((high - low) / 2) // Note: not (low + high) / 2 !!
if (A[mid]> value)
return BinarySearch(A, value, low, mid-1)
else if (A[mid] <value)
return BinarySearch(A, value, mid+1, high)
else
return mid // found
}
پیادهسازی متداول این تابع توسط الگوریتم بازگشتی در سی شارپ به صورت زیر میباشد:
static bool BinarySearch(int[] A, int x, int i, int j) {
if (i> j)
return false;
int m = (i + j) / 2;
if (x> A[m])
return BinarySearch(A, x, m + 1, j);
else if (x <A[m])
return BinarySearch(A, x, i, m - 1);
else
return true;
}
دیگر کاربردها[ویرایش]
یافتن عنصر سمت چپ[ویرایش]
برای یافتن عنصر سمت چپ عنصر مورد نظرمان یعنی T در آرایه A به ترتیب زیر عمل میکنیم:
1.به ترتیب به L و R مقادیر اولیه 0 و n را می دهیم.
2.تا زمانیکه L<R باشد مراحل زیر را تکرار میکنیم:
2.1.مقدار را به m نسبت می دهیم که همان جزء صحیح می باشد.
2.2.اگر باشد،L مقدار m-1 را میگیرد.
2.3.اگر باشد،R مقدار m را میگیرد.
3.مقدار L خروجی داده می شود.
شبه کد زیر این مراحل را نشان می دهد:
binary_search_leftmost(A, n, T):
L = 0
R = n
while L < R:
m = floor((L + R) / 2)
if A[m] < T:
L = m + 1
else:
R = m
return Lیافتن عنصر سمت راست[ویرایش]
برای یافتن عنصر سمت چپ عنصر مورد نظرمان یعنی T در آرایه A به ترتیب زیر عمل میکنیم:
1.به ترتیب به L و R مقادیر اولیه 0 و n را می دهیم.
2.تا زمانیکه L<R باشد مراحل زیر را تکرار میکنیم:
2.1.مقدار را به m نسبت می دهیم که همان جزء صحیح می باشد.
2.2.اگر باشد،R مقدار m را میگیرد.
2.3.اگر باشد،L مقدار m+1 را میگیرد.
3.مقدار R-1 خروجی داده می شود.
شبه کد زیر این مراحل را نشان می دهد:
binary_search_rightmost(A, n, T):
L = 0
R = n
while L < R:
m = floor((L + R) / 2)
if A[m] > T:
R = m
else:
L = m + 1
return R - 1منابع[ویرایش]
- دانلد کنوت. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Section 6.2.1: Searching an Ordered Table, pp. 409–426.
- Kruse, Robert L. : "Data Structures and Program Design in C++", Prentice-Hall, 1999, ISBN 0-13-768995-0, page 280.
- http://en.wikipedia.org/wiki/Binary_search_algorithm
















![{\displaystyle A[k]>x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ec4e1f5635c27809285b8401b6538e67f09e752)
![{\displaystyle A[k]\leq x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/531f6819f90ad481db6cc784d63acf3528a2b26d)

![{\displaystyle A[i]=x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a71fff78536a3422112515faafcf68dd718b06ad)


![{\displaystyle A[m]<T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73db3053a67cc299a606f9ca4fa22b688f673b49)
![{\displaystyle A[m]\geq T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/deb55a8f2705b9858658ca5a3c5e4cd0a604de6b)
![{\displaystyle A[m]>T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9b15fa5289debfa6fd8212ddadd7a430ea99d23)
![{\displaystyle A[m]\leq T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bdbc763d77a876f9ea1025e3d33695ecdd70351)