اتوماتون پشتهای
اتوماتون پشتهای صوریسازی این مفهوم شهودی، یک تعریف دقیق از آتاماتون پشتهای بدست میدهد. تعریف: یک پذیرندهٔ پشتهای غیر قطعی(NPDA) به شکل ( M=(Q،∑، Γ، ∂،qo،z،F
نمایش داده میشود، بطوریکه در آن
- Qیک مجموعه متناهی از حالتهای داخلی واحد کنترل است،
- ∑الفبای ورودی است،
- Γ یک مجموعه متناهی از نشانهها که الفبای پشته نامیده میشود،
- (∂:Q×(∑υ{⋋})×Γ تابع انتقال،
- Q0€Q حالت اولیه واحد کنترل است،
- z€Γ≤Qنشانهٔ شروع پشته است
شکل پیچیده دامنه و برد تابع انتقال نیاز به بررسی بیشتری دارد.آرگومان ∂ حالتهای فعلی واحد کنترل، نشانه ورودی فعلی و نشانهٔ بالای پشته است.نتیجه یک مجموعه از زوجهای (q،x) میباشد که در آن q حالت بعدی در واحد کنترل است.رشتهٔ x نیز به جای نشانهای که اکنون بر روی پشته است قرار میگیرد.به خاطر داشته باشیم که دومین آرگومان∂ ممکن است برابر با⋋ باشد؛ بنابراین حرکتی که هیچ نشانهای را از ورودی مصرف نمیکند امکانپذیر است. به چنین حرکتی، یک انتقال -⋋ گفته میشود.همچنین ∂ طوری تعریف شدهاست که به نشانهٔ موجود بر روی پشته نیاز دارد. اگر پشته خالی باشد هیچ حرکتی ممکن نیست.بالاخره اینکه، برد تابع انتقال یابد باید یک زیرمجموعه محدود باشد زیرا Q×Γ نامتناهی بوده و بنابراین دارای تعداد نامتناهای زیرمجموعه است. در حالیکه یک npda ممکن است. انتخابهای زیادی برای حرکت داشته باشد، این انتخابها باید به یک مجموعه متناهی از حالتها محدود باشد. فرض کنید که مجموعهٔ قانونهای انتقال یک npdaشامل ∂(q1،a،b)={(q2،cd)،(q3،⋋) باشد . اگر در یک لحظهٔ مشخص، واحد کنترل در حالت q1، نشانه ورودی برابر با a و نشانه موجود در بالای پشته نیز برابر با b باشد، یکی از دو مورد زیر اتقاف می افتد: 1)واحد کنترل به حالت q2 میرودو رشتهٔ cd جایگزین نشانهٔ بالای پشته میشود. 2)واحد کنترل به حالت q3 میشود و نشانهٔ b نیز از بالای پشته حذف میشود. در این روش نشانه گذاری، اضافه کردن یک رشته به پشته، به صورت نشانه به نشانه و از انتهای راست آن رشته انجام میشود.
عملکرد[ویرایش]

اتومات پشتهای با ماشینهای حالات متناهی در دو چیز متفاوت اند:
1-آنها میتوانند از قسمت بالا پشته استفاده کنند
که کدان انتقال صورت گیرد.
2-آنها میتوانند پشته را به عنوان بخشی از انجام
انتقال دستکاری کنند.
اتوماتون پشتهای انتقال را انتخاب میکند که با نمایهسازی یک جدول توسط سیگنال ورودی، وضعیت فعلی و نماد در بالای پشته است.این به این معنا است که این سه پارامتر مسیر انتقال را انتخاب میکنند.ماشینهای وضیعت محدود تنها به سیگنالهای ورودی وحالت حاضر نگاه میکنند.اتومات پشته ای, پشتهای را به عنوان پارامتری برای انتخاب اضافه میکنند.
انوماتون پشتهای میتواند بخشی از پشته را برای انتقال دستکاری کنند.ماشینهای وضیعت محدود حالت جدیدی را که نتیجه انتقال است را انتخاب میکند.دستکاریها یا میتوانند به صورت وارد یا خارج کردن نماد خاصی از پشته باشد.دستکاری شدن یا نشدن توسط جدول انتقال معلوم میشود.
با هم شدن:با توجه به سیگنال ورودی، وضعیت فعلی و نماد پشته،اتومات میتواند دنبال کند انتقال را به حالت دیگر و به صورت اختیاری پشته را دستکاری کند.
بهطور کلی اتوماتون پشتهای ممکن است محاسبات متعددی روی سیگنالهای ورودی انجام دهد.اگر در هر موقعیت فقط یک انتقال برای ادامه محاسبات باشد در آن صورت نتیجه اتوماتون پشتهای قطعی است.(DPDA) در غیر این صورت اتوماتون پشتهای غیر قطعی میشود(NDPDA) .تنها در گرامر مستقل از متن میشود گرامرهای مبهم را از طریق DPDA یعنی گرامرمستقل از متن قطعی,شناخت.تمام گرامرهای مستقل از متن , قطعی نیستند و مشکل شناخت گرامر مستقل از متن قطعی حل نشدهاست.[۱] به عنوان یک نتیجه از بالا DPDA یک نوع به شدت ضعیف تر از PDA است و هیچ الگوریتم برای تبدیل PDA به معادل DPDA وجود ندارد.
اگرما اجازه دسترسی به 2 پشته به جای یک پشته داشتیم آنگاه وسیلهای قوی به مانند ماشین تورینگ داشتیم.اتوماتون خطی محدود ابزاری قوی تر از اتوماتون پشتهای است ولی از ماشین تورینگ ضعیف تر است.
تعریف رسمی[ویرایش]
مااز نمادهای استاندارد زبان رسمی استفاده میکنیم: به رشتهای از حروف و و به رشتهای خالی اشاره میکند.
یک PDA عموماً با 7 عنصر مشخص میشود:
که :
- مجموعه محدودی از حالت هاست.
- مجموعه محدودی است که الفبای ورودی میگویند.
- مجموعه محدودی است که الفبای پشته گویند.
- زیرمجموعهای از (رابطه انتقال)
- حالت آغازین.
- نماد پشته اولیه.
- مجموعهای از حالات پذیرفته شده.
عنصر تابع انتقال است.
- تابع انتقال است.
محاسبات[ویرایش]
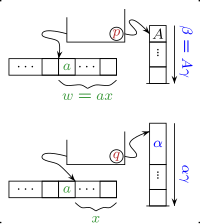
به منظور معناشناسی از ماشین پایین فشردنی شرح وضعیت فعلی معرفی شدهاست.هر سه عنصر شرح لخظهای گویند(ID), که شامل حالت کنونی و قسمتی از نوار ورودی که خوانده نشدهاست و محتویات پشته میشود.رایطه انتقال رابطه گام به گام of در هر لحظه تعریف میکند.برای ساختار مرحله , برای هر و هر وجود دارد.
اتوماتون پشتهای عموماً تبعیض ناپذیرند که در حالت لحظهای چندین راه ممکن است باشد.هر کدام از این روشها ممکن است انتخاب شوند.با تعاریف بالا در هر مرحله سمبل منفرد از بالای پشته خارج میشود و با نمادهایی که لازم تر است جایگزین میشود.به عنوان نتیجه هیچ مرحلهای که زمانی پشته خالی است انجام نمیشود.
محاسبات اتوماتون پشتهای دنبالهای از مراحل است.محاسبات با حالت اولیه و سمبل پشتهای اولیه و رشته ورودی آغاز میشود, بنابراین در حالت اولیه داریم .دو حالت پذیرش اولیه داریم.روش دیگر پذیرش از طریق حالت نهایی است.به این معنی است که پس از خواندن ورودی آن ماشین به یک حالت مورد قبول میرسد یا به وسیله پشته خالی پذیرش میشود.حالت پذیرش برای اولین بار با استفاده از حافظه داخلی و حلت دوم توسط حافظه خارجی است.
بعبارت دیگر تعریف کنیم:
- و با
- با
برای هر اتوماتون پشتهای این دو رابطه ربطی به هم ندارند.شاید در بعضی جاها با هم برابر باشند ولی دلیلی بر یکی بودن نیست.مشخصات ماشین نیز باید حالت مورد نظر را پذیرش میباشد.در تمامی اتوماتون پشتهای 2 حالت پذیرش بیانگر زبان یکیاند.
توصیف آنی[ویرایش]
توصیف آنی یک سهتایی منظم به فرم (q,w,α) است که در آن:
- 1- q یک حالت باشد.
- 2- w باقیماندهٔ رشتهٔ ورودی باشد.
- 3- α محتویات پشته باشد.
را یک توصیف آنی از ماشین پشتهای مینامیم.
- دقت کنید که در نگارش فوق سمت چپترین نماد α، بالاترین عضو پشته است. ضمناً برای نمایش حروف الفبا معمولاً از b,a,....، برای نمایش حرفهای پشته از Y,X,... و برای نمایش محتویات پشته از γ,β,αو... استفاده میشود.
مثال[ویرایش]
در پایین شرح یک PDA را داریم که زبان را از طریق حالت نهایی نشان میدهد:

)]]
, که:
متشکل از شش دستورالعملهای زیر است:
, , , , , و .
آشنایی با روند محاسبات[ویرایش]

در زیر فرق محاسبات را در رشتههای متفاوت در PDA نشان میدهیم: الف)رشته ورودی:0011 .با توجه به حرکت از حالت به حالت , انواع مختلف محاسبات داریم. و فقط یکی از اینان قبول است.
- (i) .حالت نهایی مورد پذیرش است ولی ورودی این راه خواندن را قبول نمیکند.
- (ii) .مراحل دیگر امکان پذیر نیست.
- (iii) .پذیرش محاسبه: در حالت پذیرش به پایان میرسد.، در حالی که ورودی کامل خوانده شدهاست.
ب)رشته ورودی=00111.انواع مختلف محاسبه داریم.هیچ کدام مورد قبول نیست.
- (i) .حالت نهایی مورد پذیرش است ولی ورودی این راه خواندن را قبول نمیکند.
- (ii) .مراحل دیگر امکان پذیر نیست.
- (iii) . حالت نهایی مورد پذیرش است ولی ورودی این راه خواندن را قبول نمیکند.
اتوماتون پشتهای عمومی GPDA[ویرایش]
یک نوع PDA است که رشتههایی را با طول مساوی درون پشته مینویسد و تمام رشته هارا از پشته خارج میکند.
یک GPDA 6 عنصر تعریف میشود.
- که:
, , q0 و F همان تعریف در PDA دارد و
- : تابع انتقال است.
قوانین محاسبه در GPDA مانند PDA است با این تفاوت که ai+1 و bi+1ها به جای نماد , رشته است. یکی میتواند اثبات تحلیلی برای هم ارزی از GPDA و PDAها را با استفاده از شبیهسازی زیر تدوین و فرموله کند:
Let (q1, w, x1x2...xm) (q2, y1y2...yn) be a transition of the GPDA
where , , , , , .
Construct the following transitions for the PDA:
- (q1, w, x1) (p1, )
- (p1, , x2) (p2, )
- (pm-1, , xm) (pm, )
- (pm, , ) (pm+1, yn)
- (pm+1, , ) (pm+2, yn-1)
- (pm+n-1, , ) (q2, y1)
جستارهای وابسته[ویرایش]
منابع[ویرایش]
- Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. Section 2.2: Pushdown Automata, pp. 101–114.
- Jean-Michel Autebert, Jean Berstel, Luc Boasson, Context-Free Languages and Push-Down Automata, in: G. Rozenberg, A. Salomaa (eds.), Handbook of Formal Languages, Vol. 1, Springer-Verlag, 1997, 111-174.
پیوند به بیرون[ویرایش]






































































