مجموعه مندلبرو




مجموعهٔ مندلبرو (به انگلیسی: Mandelbrot set) مجموعهای از نقطهها روی صفحهٔ مختلط است که یک فراکتال را تشکیل میدهند. این مجموعه به خاطر زیباییاش و نیز به خاطر ساختار پیچیدهای که فقط از چند تعریف سادهٔ ریاضی ناشی شده، در بیرون از دنیای ریاضیات هم شناخته شده می باشد.
تاریخچه[ویرایش]
مجموعهٔ مندلبرو اولین بار توسط یک ریاضیدان فرانسوی به نام پیر فاتو که در زمینه آنالیز مختلط پویا فعالیت میکرد در سال ۱۹۰۵ تعریف شد. فاتو در آن زمان به کامپیوتر مستعد برای ترسیم این تابع دسترسی نداشت و با وجود محاسبات زیاد نتوانست اشکالی را که ما امروزه میبینیم ببیند. همزمان ریاضیدان دیگری به نام ژولیا روی توابع گویا روی صفحهٔ اعداد مختلط کار میکرد. امروز مجموعههای ژولیا از شکلهای معروف فرکتالی است. این مباحث به صورت موضوعاتی پراکنده مطرح بودند تا این که بنوا مندلبرو در سال ۱۹۷۹ با انتشار مقالهٔ Fractals: Form, chance and dimension مباحث فوق و بسیاری از مباحث دیگر را تحت عنوان هندسه فرکتالی جمعبندی و عرضه کرد و با انتشار کتاب هندسه فرکتالی طبیعت توسط مندلبرو عملاً شکوفایی هندسهٔ فرکتالی آغاز شد.
تعریف[ویرایش]
مجموعه مندلبرو ، مرکب از «c-مقدارهای» مختلطی ست که دنبالهٔ حاصل از تکرار ترکیب تابع با خودش در نقطهٔ آغازین صفر به بینهایت میل نکند.
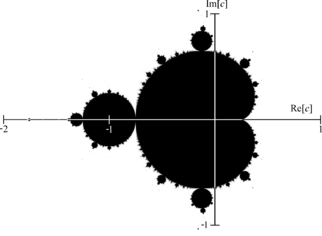
در آنالیز پویا اصطلاحاً به دنبالهای از نقاط که از تکرار ترکیب یک تابع با خودش به دست میآید ابر یا اربیت نقاط تحت آن تابع میگویند. به بیانی دیگر مجموعه مندلبرو مجموعه نقاط اربیتهای بدست آمده تحت تابع است که به بینهایت نمیگراید.
خصوصیات و قضایای مهم[ویرایش]
- قضیه(ملاک میل به بینهایت به انگلیسی The Escape Criterion): فرض کنید عضوی از مجموعه مندلبرو است اگر و تنها اگر اربیت تحت از دایرهای به شعاع ۲ و به مرکز مبدأ خارج نشود. (بیان دیگر به ازای اربیت تحت به بینهایت میل میکند)
این قضیه نشان میدهد مجموعه مندلبرو کاملاً در داخل دیسک به شعاع ۲ قرار دارد.
این مجموعه در صفحه مختلط فشرده است. همچنین دو ریاضیدان به نامهای دوادی و هابارد اثبات کردهاند که این مجموعه در صفحه پیوسته است
رنگ آمیزی تصاویر رایانهای[ویرایش]

برای خلق آثار زیبای بصری رایانهای از این فرکتال، از رنگآمیزیهای مختلف استفاده میشود و اساس آن مرتبهٔ تکرّر (iteration) است به طوری که در هر تکرار در صورت تشخیص خارج بودن نقاط از مجموعه به آن نقاط رنگ مربوط به مرتبه تکرار تعلق میگیرد. به این ترتیب تصاویر رنگی به وجود میآید.
الگوریتم ترسیم[ویرایش]
برای ترسیم فرکتال مندلبرو فلوچارت ذیل اجرا می شود :
ابتدا در صفحه اعداد مختلط عدد 0+0i به توان دو رسیده و با مختصات مورد نظری که می خواهیم بدانیم عضو مجموعه است یا خیر مانند ( 0.8i+0.2 ) جمع می شود. سپس حاصل به توان دو رسیده و با عدد موردنظر دوباره جمع می گردد .
به طور طبیعی حاصل این جمع ها پس از 60 تا 400 بار انجام این حلقه ، بزرگ شده و به سرعت از مبدا مختصات فاصله می گیرد ولی در بازه -2 تا +2 دستگاه اعداد مختلط بعضی از نقاط پس از این آزمون چندان فاصله ای از مبدا نمی گیرند . برنامه های کامپیوتری این نقاط را بر حسب تعداد انجام عمل در این حلقه رنگ می کنند و به این ترتیب تصویر مجموعه در بازه مورد نظر بر اساس این آزمون تک تک نقاط شکل گرفته و رنگ آمیزی می شود. به طور معمول برای ترسیم هر شکل ، حلقه مرکزی این آزمون بین 100 تا 300 میلیون بار انجام می شود .[۱]

منابع[ویرایش]
- https://web.archive.org/web/20070609204229/http://math.bu.edu/DYSYS/FRACGEOM/
- https://web.archive.org/web/20070429120513/http://wmi.math.u-szeged.hu/xaos/doku.php
- https://web.archive.org/web/20070418145902/http://hypertextbook.com/chaos/
- نظامالدین فقیه، آشوب و فراکتال در سیستمهای پویا ۹۶۴-۹۴۳۶۷-۱-۵:شابک[۳]
- نظامالدین فقیه، رموز تحول و توسعه در سیستمهای انسانی (نگرشی نوین) ۹۶۴-۳۵۸-۲۶۵-۵:شابک[۴][۵]
پانویس[ویرایش]
- ↑ مجله دانشمند ، شماره 351 سال 1371 ،دنیای آشوب و برخال ها : محی الدین غفرانی
- ↑ مجله دانشمند ، شماره 351 سال 1371 ،دنیای آشوب و برخال ها : محی الدین غفرانی
- ↑ Chaos and Fractals in Dynamic Systems
- ↑ رموز تحول و توسعه در سیستمهای انسانی (نگرشی نوین)[پیوند مرده]
- ↑ A Modern Cryptography of Change and Development in Human Systems
نگارخانه[ویرایش]
جستارهای وابسته[ویرایش]
پیوند به بیرون[ویرایش]
- Mandelbrot Set - Online Generator
- نرمافزار متن باز XaoS
- نرمافزار هوش مصنوعی IFS Illusions
- گاهنامه ریاضی شمار - الگوریتم مندلبروت
| در ویکیانبار پروندههایی دربارهٔ مجموعه مندلبرو موجود است. |



















