تابع همبستگی (مکانیک آماری)

نمودار تابع همبستگی اسپین مکانی برای مواد فرومغناطیس و پادفرومغناطیس، بالا و پایین دمای بحرانی نسبت به فاصله بهنجار شده نسبت به طول همبستگی. در تمام موارد، همبستگی‌ها نزدیک به مبدأ قوی هستند که حاکی از بیشترین اثر هر اسپین بر نزدیک‌ترین همسایه‌های آن است. تمام همبستگی‌ها با زیاد شدن فاصله از مبدأ به‌تدریج افت می‌کنند. بالای دمای بحرانی، هر چه فاصله بین اسپین‌ها زیاد می‌شود، همبستگی بین اسپین‌ها به صفر میل می‌کند. درحالی که پایین‌تر از دمای بحرانی، با زیاد شدن فاصله از مبدأ، همبستگی بین اسیپن‌ها به‌جای اینکه به صفر متمایل شود، به مقداری میل می‌کند که با نظم بلندبرد سیستم سازگار باشد. تفاوت در رفتار این دو کاهش، اینکه در فواصل دور از مبدأ همبستگی بین متغیرهای تصادفی میکروسکوپیک صفر می‌شود یا نه، یکی از راه‌های تعریف نظم کوتاه‌برد یا بلندبرد است.

در مکانیک آماری، تابع همبستگی (به انگلیسی: Correlation function) معیاری برای نظم موجود در یک سیستم است. درحقیقت، توابع همبستگی چگونگی ارتباط متغیرهای میکروسکوپیک مانند اسیپن و چگالی در نقاط مختلف را توصیف می‌کنند. به‌طور ویژه، توابع همبستگی بیان‌کننده این هستند که به‌طور کمی، متغیرهای میکروسکوپیک به‌طور متوسط چگونه به یکدیگر در بستر فضا و زمان همبسته هستند. یک مثال کلاسیک از این دسته از توابع فضایی را در مواد فرومغناطیس و پادفرومغناطیس می‌توان یافت که در آن‌ها به ترتیب، اسپین‌ها ترجیح می‌دهند که نسبت به نزدیک‌ترین همسایه‌هایشان هم‌جهت یا در خلاف جهت قرار گیرند. همبستگی فضایی بین اسپین‌ها در چنین موادی در شکل سمت چپ نشان داده شده‌است.

تعاریف

رایج‌ترین تعریف از تابع همبستگی برای دو متغیر تصادفی ${\displaystyle }$ و ${\displaystyle }$ در مکان‌های ${\displaystyle }$ و ${\displaystyle }$ و زمان‌های ${\displaystyle }$ و ${\displaystyle }$ برابر است با متوسط هنگرد بندادی ضرب داخلی آن دو: ${\displaystyle }$ $C(r,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle \,.$ ${\displaystyle }$ که در اینجا نماد براکت، $\langle ...\rangle$، به معنای میانگین‌گیری دمایی است. بنابر قرار داد، در حوزه‌های مختلف علوم، علامت تابع همبستگی متفاوت است. بیشترین استفاده از تابع همبستگی برای زمانی است که $s_{1}$ و $s_{2}$ هر دو یک متغیر را توصیف کنند. به عنوان مثال، تابع همبستگی اسپین-اسپین یا تابع همبستگی مکان-مکان برای یک ذره در یک مایع یا جامد (که معمولاً از آن با نام تابع توزیع شعاعی یا تابع همبستگی دوتایی یاد می‌شود) توابع همبستگی بین یک متغیر را توابع خودهمبستگی می‌گویند. با این وجود در مکانیک آماری، همه توابع همبستگی، خودهمبستگی نیستند. به‌عنوان مثال، در فازهای چندمولفه‌ای چگال شده مواد، چیزی که مورد علاقه است تابع همبستگی دوتایی بین مؤلفه‌های مختلف است.

توابع همبستگی فضایی تعادلی

غالباً علاقه‌مند هستیم که تأثیر فضایی یک متغیر تصادفی، مثلاً جهت یک اسپین، را بر محیط پیرامونش مستقل از زمان‌های بعد $\tau$. برای این منظور، در چنین مواردی، تحول زمانی سیستم را نادیده می‌گیریم و تعریف بالا را با $\tau =0$ بازنویسی می‌کنیم؛ بنابراین تابع همبستگی هم‌زمان یا فضایی $C(r,0)$ برابر خواهد شد با:

$C(r,0)=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t)\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t)\rangle \,.$

معمولاً زمان مرجع $t$, و مکان مرجع $R$ با فرض تعادل (و در نتیجه ناوردا بودن زمانی هنگرد) در نظر گرفته نمی‌شود با متوسط گرفت روی همه مکان‌های نمونه، خواهیم داشت:

$C(r)=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (r)\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (r)\rangle \,.$

که مجدداً علامت عبارت فوق قرارداد است. تابع توزیع شعاعی مثالی از تابع همبستگی فضایی است که معمولاً در آن جمله غیرهمبسته وجود ندارد. سایر توابع همبستگی فضایی اسپین-اسپین در صفحه برای مواد و شرایط گوناگونی نمایش داده شده‌اند.

توابع همبستگی زمانی تعادلی

گاهی علاقه‌مند به تحول زمانی متغیرهای میکروسکوپیک هستیم، به عبارت دیگر، می‌خواهیم بدانیم که مقدار متغیر میکروسکوپیکی در مکان $R$ و زمان $t$, چه تأثیری بر مقدار آن در زمان $t+\tau$ این توابع همبستگی زمانی توسط $C(0,\tau )$ شابه با تابع همبستگی مکانی مشخص می‌شوند با این تفاوت که وابستگی مکانی را در نظر نمی‌گیریم. با قرار دادن $r=0$, خواهیم داشت:

$C(0,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R,t+\tau )\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R,t+\tau )\rangle \,.$

با فرض تعادل (و در نتیجه ناوردا بودن زمانی هنگرد) و متوسط‌گیری روی همه خانه‌ها در نمونه مورد نظر، به رابطه ساده‌تری خواهیم رسید:

$C(\tau )=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (\tau )\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (\tau )\rangle \,.$

فرض فوق، ممکن است که در نگاه اول بدیهی به‌نظر نرسد: چگونه هنگردی که زمان-ناورداست می‌تواند تابع همبستگی زمانی غیریکنواخت داشته باشد؟ صحبت از همبستگی‌های زمانی برای سیستم‌های در حال تعادل معنی‌دار است چرا که یک هنگرد 'ماکروسکوپیک' کماکان می‌تواند دینامیک زمانی غیربدیهی به‌طور 'میکروسکوپیک' داشته باشد. به‌عنوان مثال، فرایند پخش را در نظر بگیرید. یک سیستم تک‌فازه در حال تعادل، ترکیب همگن ماکروسکوپیکی دارد. با این وجود، اگر به حرکت هر یک از اتم‌های آن نگاه کنیم، افت‌وخیزهای دائمی که به خاطر حرکت‌های شبه‌تصادفی هر کدام از اتم‌ها هستند را مشاهده می‌کنیم. مکانیک آماری به ما این اجازه را می‌دهد که جملات معناداری در مورد افت‌وخیزهای زمانی این‌گونه سیستم‌های در حال تعادل بزنیم.

تعمیمی فراتر از توابع همبستگی درحال تعادل

تمام توابع همبستگی که تاکنون معرفی شده در بستر مکانیک آماری تعادلی تعریف می‌شوند. با این حال، برای سیستم‌های به‌دور از تعادل نیز می‌توانیم توابع همبستگی تعریف کنیم. با بررسی تعریف عمومی $C(r,\tau )$، واضح است که متغیرهای تصادفی به کاررفته در این توابع همبستگی مانند مکان یا اسپین اتم‌ها را می‌توان به‌دور از تعادل در نظر گرفت. آنگاه حاصل‌ضرب داخلی آن‌ها نیز به دور از بحران خوش‌تعریف خواهد بود. در این صورت عملگری که دیگر به‌دور از بحران خوش‌تعریف نیست، متوسط‌گیری روی هنگردهای تعادلی است. این فرایند متوسط‌گیری برای سیستم‌های غیرتعادلی توسط متوسط‌گیری از ضرب داخلی روی کل نمونه جایگزین می‌شود. این کار در آزمایش‌های پراکندگی و شبیه‌سازی‌های رایانه‌ای متداول است و اغلب برای اندازه‌گیری تابع توزیع شعاعی شیشه‌ها به کار می‌رود.

اندازه‌گیری توابع همبستگی

توابع همبستگی، $C(r,\tau =0)$، به عنوان تابعی از شعاع برای یک سیستم اسپینی فرومغناطیس بالا و پایین دمای بحرانی $T_{C}$. بالای دمای بحرانی، تابع همبستگی، ترکیبی از یک وابستگی نمایی و قانون-توانی نسبت به فاصله است. $C(r,\tau =0)\propto r^{-(d-2+\eta )}e^{-r/\xi (T)}$. در فواصل نزدیک (نسبت به طول همبستگی $\xi$)، وابستگی قانون توانی، رفتار غالب و در فواصل دور، وابستگی نمایی رفتار غالب را دارد. در دمای بحرانی $T_{C}$، طول همبستگی واگرا می‌شود $\xi (T_{C})=\infty$ که به تنهایی سبب رفتار توانی می‌شود: $C(r,\tau =0)\propto r^{-(d-2+\eta )}$. دمای بحرانی، $T_{C}$، توسط ناموضعیت شدید طول همبستگی مکانی بین مقادیر میکروسکوپیک پارامتر نظم مربوط بدون نظم بلندبرد قابل تمیز است. زیر $T_{C}$، اسپین‌ها یک نظم خودبه‌خودی نشان می‌دهند و بنابراین طول همبستگی بی‌نهایت است. گذارفازهای پیوسته نظم-بی‌نظم را می‌توان به عنوان فرایندی دانست که طی آن، $\xi$ از مقداری نامتناهی در حالت منظم در دمای کم به مقداری متناهی در حالت نامنظم در دمای بالا تغییر می‌کند.

توابع همبستگی معمولاً به کمک آزمایش‌های پراکندی اندازه‌گیری می‌شوند. به‌عنوان مثال، آزمایش‌های پراکندگی پرتو ایکس به‌طور مستقیم همبستگی‌های مکانکی الکترون-الکترون را اندازه‌گیری می‌کند. توابع همبستگی مکانی اسپین-اسپین توسط پراکندی نوترون اندازه‌گیری می‌شوند. همچنین به کمک پراکندگی نوترون می‌توانیم اطلاعاتی در مورد همبستگی دوتایی به‌دست آوریم.

برای سیستم‌هایی که از ذراتی با اندازه بزرگتر از یک میکرون تشکیل شده‌اند، به کمک میکروسکوپ نوری می‌توان هم همبستگی زمانی و هم همبستگی مکانی را به دست آورد. برای همین، استفاده از میکروسکوپ نوری برای سوسپانسیون‌های کلوئیدی به ویژه در ۲بعد رایج است.

تحول زمانی توابع همبستگی

لارس اونزاگر در سال ۱۹۳۱ پیشنهاد کرد که «رگرسیون افت‌وخیزهای دمایی میکروسکوپیک در تعادل، از قانون میکروسکوپیک واهلش آشفتگی‌های کوچک غیرتعادلی پیروی می‌کند.» این عبارت به فرض رگرسیون اونزاگر معروف است. از آن‌جا که مقادیر متغیرهای میکروسکوپیکی که توسط بازه‌های زمانی بزرگ $\tau$ از هم تفکیک شده‌اند باید فراتر از آنچه که ما از تعادل ترمودینامیکی انتظار داریم ناهمبسته باشند، می‌توان از نقطه نظر فیزیک به تحول زمانی تابع همبستگی چنان نگاه کرد که گویی سیستم به‌وسیله مشخص کردن یک متغیر میکروسکوپیک، رفته‌رفته «فراموش می‌کند» که شرایط اولیه‌ای که طی کرده چه بوده. در حقیقت، یک راه شهودی برای دیدن ارتباط بین تحول زمانی توابع همبستگی و تحول زمانی سیستم‌های ماکروسکوپیک وجود دارد: به‌طور متوسط، تابع همبستگی همان‌گونه در بستر زمان تحول می‌یابد که اگر سیستم در شرایطی که توسط مقدار اولیه تابع همبستگی مشخص شده بود و اجازه تحول داشت، تحول می‌یافت.

ارتباط بین گذارفازها و توابع همبستگی

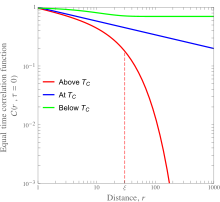
گذارفازهای پیوسته، مانند گذار نظم-بی‌نظمی در آلیاژهای فلزی و گذارهای فرومغناطیس-پارامغناطیس شامل گذاری از یک حالت منظم به یک حالت نامنظم هستند. به زبان تابع همبستگی، تابع همبستگی مکانی برای همه نقاط شبکه زیر دمای بحرانی غیرصفر است و بالای دمای بحرانی، فقط برای فاصله‌های به‌نسبت کوچک، غیرقابل چشم‌پوشی است. از آنجا که گذارفاز پیوسته‌است، هنگامی که سیستم را به قدری گرم کنیم که دمای آن فراتر از دمای بحرانی آن شود، طولی که طی آن متغیرهای میکروسکوپیک همبسته هستند، $\xi$، باید به‌طور پیوسته از بی‌نهایت به مقداری محدود تغییر کند. این سبب می‌شود تا تابع همبستگی یک وابستگی قانون-توانی از فاصله از نقطه بحرانی پیدا کند. این وابستگی برای یک ماده فرومغناطیس، در شکل سمت چپ نشان داده شده. جزئیات این شکل در بخش مغناطش آمده‌است.

کاربردها

مغناطش

تابع همبستگی مکانی در یک سیستم اسپینی به خوبی مورد مطالعه قرار گرفته‌است. این کمیت توصیف‌کنندهٔ متوسط هنگرد بندادی (آنسامبل کانونیک) حاصل‌ضرب داخلی اسپین‌ها در دو نقطه از شبکه رو تمام حالت‌های ممکن است هست:

$G(r)=\langle \mathbf {s} (R)\cdot \mathbf {s} (R+r)\rangle \ -\langle \mathbf {s} (R)\rangle \langle \mathbf {s} (R+r)\rangle \,.$

اینجا منظور از براکت <...> متوسط گرمایی است. نمودار شماتیک این تابع برای یک ماده فرومغناطیس، بالا و پایین دمای بحرانی (دمای کوری) در شکل سمت چپ نمایش داده شده‌است. حتی در یک فاز بی‌نظم از لحاظ مغناطیسی، اسپین‌ها در مکان‌های مختلف با هم همبسته هستند؛ مثلاً اگر فاصله r بسیار کوچک باشد، (در مقایسه با مقیاس مکانی $\xi$)، برهم‌کنش بین اسپین‌ها سبب می‌شود تا آن‌ها همبسته شوند. جهت‌گیری که به‌طور طبیعی به‌خاطر برهمکنش بین اسپین‌ها ایجاد می‌شود، توسط اثرات گرمایی از بین می‌رود. در دماهای بالا، با زیادشدن فاصله، کاهش همبستگی به‌صورت نمایی مشاهده می‌شود که تابع همبستگی به‌طور مجانبی با رابطهٔ زیر توصیف می‌شود:

$G(r)\approx {\frac {1}{r^{d-2+\eta }}}\exp {\left({\frac {-r}{\xi }}\right)}\,,$

که r فاصله بین اسپین‌ها، d بعد سیستم، و $\eta$ یک نمای بحرانی است. در دماهای بالا، همبستگی با زیاد شدن فاصله بین اسپین‌ها، به‌طور نمایی افت می‌کند. پایین‌تر از دمای بحرانی $T_{c}$، نیز چنان رفتار نمایی در افت همبستگی مشاهده می‌شود با این حد که در فواصل بزرگ برابر با مغناطش متوسط $\langle M^{2}\rangle$ می‌شود.

هرچه دما کاهش یابد، بی‌نظمی گرمایی کاهش می‌یابد و در یک گذار فاز پیوسته طول همبستگی واگرا می‌شود، به‌طوری که طول همبستگی باید از یک مقدار متناهی در بالای گذار فاز به‌طور پیوسته به مقداری نامتناهی در پایین گذار فاز تغییر کند:

$\xi \propto |T-T_{c}|^{-\nu }\,,$

که $\nu$ یک نمای بحرانی دیگر است.

این همبستگی قانون-توانی، مسئول بی‌مقیاسی مشاهده شده در این گذارهاست. تمام نماهایی که به آن‌ها اشاره شد مستقل از دما هستند. در حقیقت نماها جهان‌شمول یا عمومی هستند، به این معنا که برای سیستم‌های گوناگونی این نماها مقدار یکسانی دارند.

تابع توزیع شعاعی

تابع توزیع شعاعی یک تابع همبستگی رایج است که اغلب در مکانیک آماری دیده می‌شود. با استفاده از روش پراکندگی معکوس کوانتومی و حدس بیته، تابع همبستگی در برخی از مدل‌ها که دقیقاً حل‌پذیر هستند (گاز بوزونی یک‌بعدی، زنجیره‌های اسپینی و مدل هابرد) قابل حساب کردن می‌باشد.

توابع همبستگی مرتبه بالاتر

توابع همبستگی مرتبه بالاتر شامل مبدأ چندگانه می‌شوند که به سادگی توسط تعمیم رابطه قبلی، با در نظر گرفتن مقدار متوسط حاصل‌ضرب بیش از دو متغیر تصادفی قابل تعریف است:

$C_{i_{1}i_{2}\cdots i_{n}}(s_{1},s_{2},\cdots ,s_{n})=\langle X_{i_{1}}(s_{1})X_{i_{2}}(s_{2})\cdots X_{i_{n}}(s_{n})\rangle .$

با این‌وجود، تفسیر و محاسبه این‌چنین توابع همبستگی مرتبه بالاتر به نسبت کار دشواری است. برای مثال، برای اندازه‌گیری مشابه مرتبه‌بالاتر تابع‌توزیع دوتایی، چشمه‌های هم‌دوس پرتو اکس نیاز است. هم نظریه چنین تحلیل‌هایی و هم اندازه‌گیری آزمایشگاهی پرتو اکس مورد نیاز، زمینه‌های فعال پژوهش هستند.

منابع

ویکی‌پدیای انگلیسی: https://en.wikipedia.org/wiki/Correlation_function_(statistical_mechanics)

برای مطالعه بیشتر

• Sethna, James P. (2006). "Chapter 10: Correlations, response, and dissipation". Statistical Mechanics: Entropy, Order Parameters, and Complexity. Oxford University Press. ISBN 0-19-856677-8.
• Radial distribution function
• Yeomans, J. M. (1992). Statistical Mechanics of Phase Transitions. Oxford Science Publications. ISBN 0-19-851730-0.
• Fisher, M. E. (1974). "Renormalization Group in Theory of Critical Behavior". Reviews of Modern Physics. 46 (4): 597–616. Bibcode:1974RvMP...46..597F. doi:10.1103/RevModPhys.46.597.
• C. Domb, M.S. Green, J.L. Lebowitz editors, Phase Transitions and Critical Phenomena, vol. 1-20 (1972–2001), Academic Press.