تابع توزیع تجمعی

تابع توزیع تجمعی برای توزیع نرمال .

تابع چگالی احتمال برای چند توزیع نرمال، نمودار قرمز رنگ مربوط به توزیع نرمال استاندارد است ..

تابع توزیع تجمعی تابعی است غیر صفر و هم نوای صعودی که برد آن بازه [۰٫۱] بوده و احتمال آنکه متغیر تصادفی X دارای مقداری کوچک‌تر از x باشد را نشان می‌دهد، یعنی:

$x\to F_{X}(x)=\operatorname {P} (X\leq x)$

از این تعریف می‌توان نتیجه گرفت که

$P(a<X\leq b)=F_{X}(b)-F_{X}(a)$

تابع توزیع تجمعی را می‌توان به صورت زیر بر اساس تابع چگالی احتمال نیز تعریف کرد

$F(x)=\int _{-\infty }^{x}f(t)\,dt.$

در مورد متغیرهای تصادفی با مقادیر گسسته این تعریف به صورت زیر است:

$\Pr(X=x)=F(x_{0})-F(x_{0}-),$ که در اینجا $F(x_{0}-)$ به معنی حد چپ تابع $F_{X}(x)$ است وقتی که $x$ به $x_{0}$ میل می‌کند

خواص تابع توزیع تجمعی

• تابع توزیع تجمعی برای متغیر تصادفی گسسته به این شکل تعریف می شود :

$$F_{X}(x)=P(X\leq x)=\sum _{t\leq x}f(t)$$

• 
  نمودار تابع توزیع تجمعی برای متغیر تصادفی گسسته

• تعریف تابع توزیع تجمعی برای متغیر تصادفی پیوسته به این شکل می شود :

$$F_{X}(x)=P(X\leq x)=\int _{t\leq x}f(t)dt$$

• تمام توابع توزیع تجمعی صعودی (ولی نه لزوماً صعودی اکید) و از راست پیوسته هستند.

• $0\leq F_{X}(x)\leq 1$

• $\lim _{x\to -\infty }F(x)=0$

• $\lim _{x\to +\infty }F(x)=1$

• اگر $x_{1}\leq x_{2}$ باشد ، آنگاه :

$$F_{X}(x_{1})\leq F_{X}(x_{2})$$

• $P(X>x)=1-F_{X}(x)$

• $P(x_{1}<x\leq x_{2})=F_{X}(x_{2})-F_{X}(x_{1})$

• اگر M میانه داده ها باشد داریم :

$$F_{X}(M)=\int _{-\infty }^{M}f(x)dx={\frac {1}{2}}$$

و همان تعریف میانه است که نیمی از داده ها مقداری کمتر از M دارند .

مثال

فرض کنید X یک متغیر تصادفی پیوسته است که تابع چگالی احتمال آن به این شکل تعریف شده باشد :

$$f(x)={\begin{cases}0&x\leq -1\\\\x+1&-1<x\leq 0\\\\1-x&0<x<1\\\\0&x\geq 0\end{cases}}$$

نمودار چگالی احتمال این متغیر تصادفی به شکل زیر خواهد بود :

• 
  نمودار تابع چگالی احتمال

با انتگرال گیری از تابع چگالی احتمال در هر بازه تابع توزیع تجمعی آن را به دست می آوریم و خواهیم داشت :

$$F(x)={\begin{cases}0&x\leq -1\\\\{\frac {1}{2}}(x+1)^{2}&-1<x\leq 0\\\\1-{\frac {(1-x)^{2}}{2}}&0<x<1\\\\1&x\geq 0\end{cases}}$$

• 
  نمودار تابع توزیع تجمعی

تابع توزیع تجمعی برای چند توزیع

در این قسمت تابع توزیع تجمعی چند توزیع معروف و نمودار توزیع تجمعی آن ها را بررسی می کنیم :

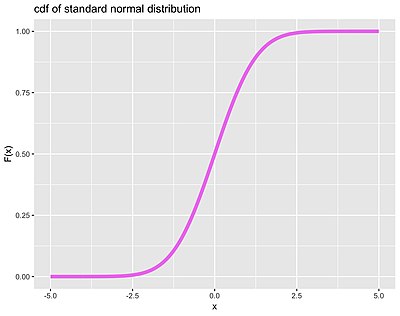
توزیع طبیعی استاندارد

تابع چگالی احتمال توزیع طبیعی استاندارد برای ℝ $x\in$ به شکل زیر تعریف می شود :

$$f(x)={\frac {1}{\sqrt {2\pi }}}e^{\frac {-x^{2}}{2}}$$

و تابع توزیع تجمعی آن برابر است با :

$$F(x)=\int f(x)dx=\int {\frac {1}{\sqrt {2\pi }}}e^{\frac {-x^{2}}{2}}={\frac {1}{2}}\left(1+{\mathrm {erf} }\,{\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\!$$

نمودار

• 
  نمودار تابع توزیع تجمعی توزیع طبیعی استاندارد

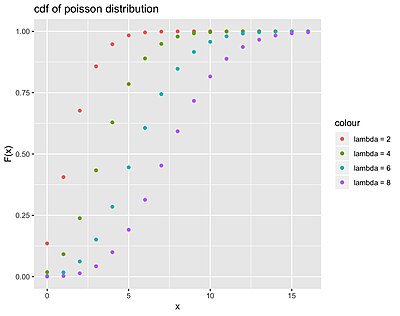
توزیع پواسون

تابع چگالی احتمال توزیع پواسون برای {1,2,3,...} $k\in$ و $\lambda \in (0,\infty )$ به شکل زیر تعریف می شود:

$$f(x)={\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}\!}$$

و تابع توزیع تجمعی آن برابر است با :

$$F(x)=\int f(x)dx=\int {\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}\!}={\displaystyle {\frac {\Gamma (k+1,\lambda )}{k!}}\!}$$

نمودار

• 
  نمودار تابع توزیع تجمعی توزیع پواسون

توزیع نمایی

تابع چگالی احتمال توزیع نمایی برای $x\geq 0$ به شکل زیر تعریف می شود :

$$f(x)=\lambda e^{-\lambda x}$$

و تابع توزیع تجمعی آن برابر است با :

$$F(x)=\int f(x)dx=\int \lambda e^{-\lambda x}=1-e^{-\lambda x}$$

نمودار

• 
  نمودار تابع توزیع تجمعی توزیع نمایی