روش سفتی مستقیم

به عنوان یکی از روش‌های تحلیل سازه، روش سفتی مستقیم (به انگلیسی: Direct stiffness method)، که با عنوان روش سفتی ماتریسی (به انگلیسی: Matrix stiffness method) نیز شناخته می‌شود، برای آنالیز رایانه ای سازه‌های پیچیده از جمله سازه‌های نامعین استاتیکی است. این یک روش ماتریسی است که از روابط سفتی اعضا برای محاسبه نیروها و جابجایی عضوها در سازه‌ها استفاده می‌کند. روش سفتی مستقیم متداول‌ترین اجرای روش المان محدود(FEM) است. در استفاده از این روش، سیستم باید به عنوان مجموعه ای از عناصر ساده‌تر و ایدئال که در گره‌ها به هم متصل شده‌اند، مدل شود. خصوصیات سفتی مواد این المان‌ها، از طریق محاسبات ماتریسی، یک معادله ماتریسی را نتیجه می‌دهد که بر رفتار کل سازهٔ ایدئال حاکم است. جابجایی‌ها و نیروهای مجهول سازه از حل این معادله بدست می‌آید. روش سفتی مستقیم اساس و پایهٔ اکثر نرم‌افزارهای منبع آزاد و تجاری المان محدود را تشکیل می‌دهد.

روش سفتی مستقیم از حوزه هوافضا سرچشمه گرفته‌است. محققان رویکردهای مختلفی را برای تحلیل فریم‌های پیچیده هواپیما مورد بررسی قرار دادند. این رویکردها شامل تئوری الاستیسیته، اصول انرژی در مکانیک ساختاری، روش انعطاف‌پذیری و روش سفتی ماتریسی بود. از طریق تحلیل این متدها، روش سفتی مستقیم به عنوان روشی کارآمد که به‌طور ایدئال برای اجرای کامپیوتر مناسب است، بدست آمد.

تاریخچه

بین سال‌های ۱۹۳۴ و ۱۹۳۸، AR Collar و W.J. Duncan اولین مقالات را با نمایندگی و اصطلاحات مربوط به سیستم‌های ماتریسی منتشر کردند که امروزه مورد استفاده قرار می‌گیرند. تحقیقات هواکشسانی تا جنگ جهانی دوم ادامه یافت، اما محدودیت‌های انتشار از ۱۹۳۸ تا ۱۹۴۷ ردیابی این آثار را دشوار کرده‌است. دومین موفقیت بزرگ در تحلیل ماتریسی سازه‌ها در سال ۱۹۵۴ و ۱۹۵۵ رخ داد که پروفسور جان H. Argyris مفهوم مونتاژ (سرهم‌بندی) المان‌های عنصری یک سازه را به یک سیستم معادلات تبدیل کرد. سرانجام، در ۶ نوامبر ۱۹۵۹، MJ Turner، رئیس واحد دینامیک سازهٔ Boeing، مقاله ای را منتشر کرد که در آن روش سفتی مستقیم را به عنوان یک الگوی کارآمد برای پیاده‌سازی رایانه‌ای نشان می‌دهد. (Felippa 2001).

روابط سفتی اعضا

رابطهٔ رایج برای سفتی یک عضو فرم کلی زیر را دارد:

$\mathbf {Q} ^{m}=\mathbf {k} ^{m}\mathbf {q} ^{m}+\mathbf {Q} ^{om}\qquad \qquad \qquad \mathrm {(1)}$

که در آن

m = عضو شماره m.

$\mathbf {Q} ^{m}$ = بردار نیروهای هر عضو، که نیروهای مجهول داخلی هستند.

$\mathbf {k} ^{m}$ = ماتریس سختی عضو که مشخص کننده مقاومت عضو در برابر تغییر شکل است.

$\mathbf {q} ^{m}$ = بردار جابجایی‌ها یا تغییر شکل‌های هر عضو.

$\mathbf {Q} ^{om}$ = بردار نیروهای خارجی هر عضو، ناشی از اثرات خارجی (مانند نیروهای معلوم و تغییرات دما) که در هنگام $\mathbf {q} ^{m}=0$ به عضو وارد می‌شود.

اگر $\mathbf {q} ^{m}$ بیانگر تغییر شکل اعضا باشد، به جای جابجایی مطلق، آنگاه $\mathbf {Q} ^{m}$ بیانگر نیروهای مستقل اعضا می‌باشد، و در این حالت رابطهٔ (۱) به رابطه‌ای برای به دست آوردن ماتریس انعطاف‌پذیری عضو، که در روش انعطاف‌پذیری استفاده می‌شود، تبدیل شود.

رابطه سفتی سیستم

برای یک سیستم که از تعداد زیادی عضو تشکیل شده که در نقاطی به نام گره به یکدیگر متصل شده‌اند. روابط سفتی اعضا از جمله معادله (۱) با استفاده از نکات زیر می‌تواند جمع شود:

• تغییر شکل اعضا($\mathbf {q} ^{m}$) را می‌تواند با ترم‌هایی مربوط به جابجایی گره‌های سیستم(r) بیان کرد، تا سازگاری بین اعضا بیان شود. این بدان معنی است که r مجهول اصلی خواهد بود.
• نیروهای اعضا ($\mathbf {Q} ^{m}$) به نگه داشتن گره‌ها در حالت تعادل تحت نیروهای گره (R) کمک می‌کند. این بدان معنی است که سمت راست معادله (۱) در سمت راست معادلات تعادل گره برای کل سیستم ادغام می‌شود:

$\mathbf {R} =\mathbf {Kr} +\mathbf {R} ^{o}\qquad \qquad \qquad \mathrm {(2)}$

که در آن:

$\mathbf {R}$ = بردار نیروهای گره ای، نشان‌دهندهٔ نیروهای خارجی اعمال شده روی گره‌ها.

$\mathbf {K}$ = ماتریس سفتی سیستم، که از مجموع ماتریس‌های سختی اعضا ($\mathbf {k} ^{m}$) بدست می‌آید.

$\mathbf {r}$ = بردار جابجایی‌های گره ای سیستم که می‌تواند تمام پیکربندی‌های تغییر شکل احتمالی (هر نوع تغییر شکلی در سیستم) سیستم را تحت نیروهای دلخواه گره R تعریف کند.

$\mathbf {R} ^{o}$ = بردار نیروهای گره معادل، نمایانگر تمام تأثیرات خارجی به غیر از نیروهای گره ای است که قبلاً در بردار نیروی گره ای R به حساب آورده شده‌است. این بردار از جمع $\mathbf {Q} ^{om}$ اعضا بدست می‌آید.

راه حل

ماتریس سفتی سیستم K، ماتریسی مربعی است زیرا بردارهای R و r اندازه یکسان دارند. علاوه بر این، این ماتریس متقارن (سیمتریک) است زیرا $\mathbf {k} ^{m}$ متقارن است. هنگامی که قیدهای کمکی در معادله (۲) اعمال شود، جابجایی گره‌ها از حل دستگاه معادلات خطی (۲)، به صورت نمادین یافت می‌شود:

$\mathbf {r} =\mathbf {K} ^{-1}(\mathbf {R} -\mathbf {R} ^{o})\qquad \qquad \qquad \mathrm {(3)}$

در ادامه، نیروهای مشخصه اعضا ممکن است از معادله (۱) یافت شود؛ که در آن $\mathbf {q} ^{m}$ را با درنظر گرفتن مطابقت می‌توان از r یافت.

روش سختی مستقیم

معمول است که معادلات (۱) را به شکلی نوشت که در آن $\mathbf {q} ^{m}$ و $\mathbf {Q} ^{om}$ به ترتیب، جابجایی‌ها و نیروهای اعضا مطابق با r و R هستند. در چنین موردی ، $\mathbf {K}$ و $\mathbf {R} ^{o}$ را می‌توان از جمع کردن مستقیم ماتریس اعضا ($\mathbf {k} ^{m}$ و $\mathbf {Q} ^{om}$) بدست آورد. این روش به عنوان روش سفتی مستقیم شناخته می‌شود.

مزایا و معایب روش سفتی ماتریسی در مقاله روش انعطاف‌پذیری مقایسه و مورد بحث واقع شده.

مثال

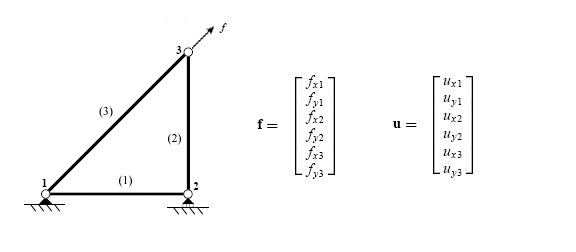
درهم شکستن

اولین گام دراستفاده از روش سختی مستقیم، شناسایی المان‌های مجزایی است که سازه را تشکیل می‌دهند.

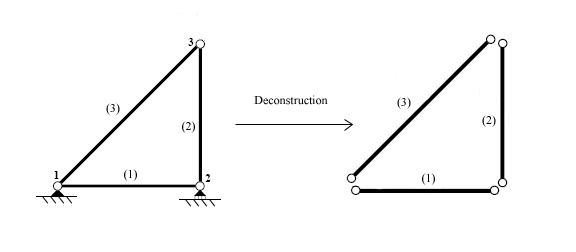
بعد از اینکه المان‌ها معین شدند، سازه در گره‌ها از هم جدا می‌شود، گره‌ها نقاطی هستند که در آن نقاط المان‌های مختلف به یکدیگر متصل می‌شوند.

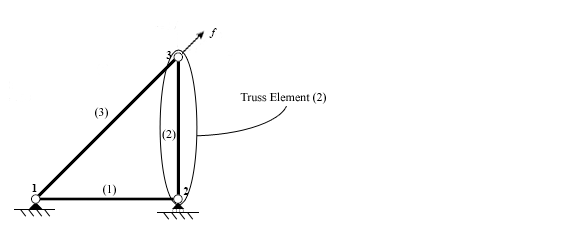
سپس هر المان به صورت جداگانه تحلیل می‌شود تا معادلات سفتی عضو را توسعه دهد. نیروها و جابجایی‌ها از طریق ماتریس سفتی المان به هم وابسته هستند که این ماتریس به هندسه و خصوصیات هر المان بستگی دارد.

یک المان خرپا فقط می‌تواند نیروها را به‌طور فشاری یا کششی منتقل کند. این بدان معنی است که در دو بعد، هر گره دارای دو درجه آزادی (DOF) است: جابجایی افقی و عمودی. معادله حاصل شامل یک ماتریس سفتی چهار در چهار است.

${\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}\\k_{21}&k_{22}&k_{23}&k_{24}\\k_{31}&k_{32}&k_{33}&k_{34}\\k_{41}&k_{42}&k_{43}&k_{44}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}$

یک المان قاب علاوه بر نیروی کششی و فشاری، قادر به مقاومت در برابر ممان‌های خمشی هم می‌باشد. در نتیجه سه درجه آزادی دارد: جابه جایی افقی و عمودی و چرخش صفحه‌ای. در این مورد ماتریس سفتی، ماتریسی ۶ در ۶ است.

${\begin{bmatrix}f_{x1}\\f_{y1}\\m_{z1}\\f_{x2}\\f_{y2}\\m_{z2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}&k_{15}&k_{16}\\k_{21}&k_{22}&k_{23}&k_{24}&k_{25}&k_{26}\\k_{31}&k_{32}&k_{33}&k_{34}&k_{35}&k_{36}\\k_{41}&k_{42}&k_{43}&k_{44}&k_{45}&k_{46}\\k_{51}&k_{52}&k_{53}&k_{54}&k_{55}&k_{56}\\k_{61}&k_{62}&k_{63}&k_{64}&k_{65}&k_{66}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\\theta _{z1}\\u_{x2}\\u_{y2}\\\theta _{z2}\\\end{bmatrix}}$

المان‌های دیگر مانند صفحه‌ها و پوسته‌ها نیز می‌توانند در روش سفتی مستقیم گنجانیده شوند و معادلات مشابهی باید ایجاد شوند.

مونتاژ

پس از بسط روابط فردی سفتی هر المان، آنها باید در سازه اصلی مونتاژ شوند. اولین قدم در این فرایند تبدیل کردن روابط سفتی المان‌ها به یک سیستم جهانی برای کل سازه است. در مورد یک المان خرپا، شکل جهانی روش سفتی بستگی به زاویه این المان با توجه به سیستم مختصات جهانی دارد (این سیستم معمولاً سیستم مختصات دکارتی است).

${\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\frac {EA}{L}}{\begin{bmatrix}c^{2}&sc&-c^{2}&-sc\\sc&s^{2}&-sc&-s^{2}\\-c^{2}&-sc&c^{2}&sc\\-sc&-s^{2}&sc&s^{2}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}{\begin{array}{r }s=\sin \beta \\c=\cos \beta \\\end{array}}$ (برای یک عنصر خرپا با زاویه β) معادل ، $\left[{\begin{array}{c}f_{x1}\\f_{y1}\\\hline f_{x2}\\f_{y2}\\\end{array}}\right]={\frac {EA}{L}}\left[{\begin{array}{c c|c c}c_{x}c_{x}&c_{x}c_{y}&-c_{x}c_{x}&-c_{x}c_{y}\\c_{y}c_{x}&c_{y}c_{y}&-c_{y}c_{x}&-c_{y}c_{y}\\\hline -c_{x}c_{x}&-c_{x}c_{y}&c_{x}c_{x}&c_{x}c_{y}\\-c_{y}c_{x}&-c_{y}c_{y}&c_{y}c_{x}&c_{y}c_{y}\\\end{array}}\right]\left[{\begin{array}{c}u_{x1}\\u_{y1}\\\hline u_{x2}\\u_{y2}\\\end{array}}\right]$

که در آن $c_{x}$ و $c_{y}$ کسینوس‌های عنصر خرپا در جهت ایکس و وای هستند (یعنی آنها اجزای یک بردار واحد هستند که با عضو هماهنگ هستند). این فرم چگونگی تعمیم سفتی عنصر به خرپاهای فضایی ۳ بعدی را با ساده کردن الگویی که در این فرمول مشهود است نشان می‌دهد.

پس از ایجاد ماتریس سفتی عنصر در سیستم مختصات جهانی، آنها باید در یک ماتریس سختی «مستر» یا «جهانی» ادغام شوند. در هنگام ادغام این ماتریس‌ها دو قانون وجود دارد که باید رعایت شود: مطابقت جابجایی‌ها و تعادل نیرو در هر گره. این قوانین با اتصال جابجایی گره المان به جابجایی‌های گره جهانی رعایت می‌شوند.

بردارهای جابجایی جهانی و بردار نیروی جهانی، هر کدام به ازای هر درجه آزادی در سازه دارای یک ورودی هستند. ماتریس‌های سفتی المان با تقویت یا گسترش هر ماتریس در سازگاری با بردارهای جابجایی و بارگذاری جهانی ادغام می‌شوند.

$k^{(1)}={\frac {EA}{L}}{\begin{bmatrix}1&0&-1&0\\0&0&0&0\\-1&0&1&0\\0&0&0&0\\\end{bmatrix}}\rightarrow K^{(1)}={\frac {EA}{L}}{\begin{bmatrix}1&0&-1&0&0&0\\0&0&0&0&0&0\\-1&0&1&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\\end{bmatrix}}$ (برای عنصر (۱) ساختار فوق)

سرانجام، ماتریس سفتی جهانی با اضافه کردن ماتریس‌های فردی بسط یافته هر المان به یکدیگر ساخته می‌شود.

راه حل

هنگامی که ماتریس سفتی کلی، بردار جابجایی و بردار نیرو ساخته شد، سیستم می‌تواند با یک معادله ماتریسی بیان شود.

برای هر درجه از آزادی در سازه، یا جابجایی یا نیرو معلوم است.

پس از درج مقدار معلوم برای هر درجه از آزادی، معادله سفتی مستر، کامل و آماده ارزیابی است. چندین روش مختلف برای ارزیابی یک معادله ماتریسی در دسترس است که شامل محدودیت در تجزیه Cholesky و ارزیابی نیروی خالص سیستم معادلات نیست. اگر یک سازه به درستی مهار نشود، اعمال یک نیرو باعث می‌شود که آن به صورت صلب حرکت کند و قیود اضافی باید اضافه شود.

روشی که در این بخش شرح داده شد، نگاهی کلی بر روش سفتی مستقیم است. برای اطلاعات بیشتر در مورد فرایند و همچنین فرضیات در مورد خواص مادهٔ دخیل در فرایند باید از منابع اضافی استفاده شود.

کاربردها

روش سفتی مستقیم به‌طور اختصاصی برای پیاده‌سازی مؤثر و آسان نرم‌افزارهای رایانه ای برای ارزیابی سازه‌های پیچیده که شامل تعداد زیادی عضو است، ساخته شده‌است. امروزه، تقریباً هر حل‌کنندهٔ المان محدود موجود بر اساس روش سفتی مستقیم است. در حالی که هر برنامه از یک فرایند یکسان استفاده می‌کند، بسیاری از آنها برای کاهش زمان محاسبه و کاهش حافظه مورد نیاز اصلاح شده‌اند. برای دستیابی به این هدف، میانبرهایی ایجاد شده‌است.

یکی از بزرگترین حوزه‌ها برای استفاده از روش سفتی مستقیم حوزهٔ تحلیل ساختاری است که این روش در نرم‌افزار مدل‌سازی گنجانیده شده‌است. این نرم‌افزار به کاربران اجازه می‌دهد تا یک سازه را مدلسازی کنند و پس از تعریف کاربر از خواص مواد عناصر، این برنامه به‌طور خودکار روابط عناصر و سختی جهانی را ایجاد می‌کند. هنگامی که شرایط بارگیری مختلفی اعمال می‌شود، نرم‌افزار ساختار را ارزیابی می‌کند و برای کاربر خیزها را نمایش می‌دهد.

جستارهای وابسته

• روش المان محدود
• روش المان محدود در مکانیک سازه
• تحلیل سازه
• روش انعطاف‌پذیری
• لیست بسته‌های نرم‌افزاری المان محدود

منابع

• Felippa, Carlos A. (2001), "A historical outline of matrix structural analysis: a play in three acts" (PDF), Computers & Structures, 79 (14): 1313–1324, doi:10.1016/S0045-7949(01)00025-6, ISSN 0045-7949, archived from the original (PDF) on 2007-06-29, retrieved 2005-10-05
• Felippa , Carlos A. مقدمه ای از روش عنصر محدود. پاییز ۲۰۰۱ دانشگاه کلرادو ۱۸ سپتامبر ۲۰۰۵
• رابینسون، جان. آنالیز ماتریس ساختاری برای مهندس. نیویورک: جان ویلی و پسران، ۱۹۶۶
• Rubinstein, Moshe F. Matrix تجزیه و تحلیل کامپیوتر ساختارها. New Jersey: Prentice-Hall، ۱۹۶۶
• McGuire, W. ، Gallagher, RH, and Ziemian, RD Structural Analysis Structural، 2nd Ed. نیویورک: جان ویلی و پسران، ۲۰۰۰.

پیوند به بیرون

• استفاده از روش سختی مستقیم در سیستم بهار ۱ بعدی
• تحلیل ماتریسی سازه
• انیمیشن‌های شبیه‌سازی تحلیل سختی