مورچه لنگتون

مورچهٔ لنگتون گونه‌ای خاص از ترمایت (نوعی ماشین محاسبهٔ تورینگ دو بعدی) است که در سال ۱۹۸۶ توسط کریس لنگتون ابداع شده‌است، همچنین می‌توان مورچهٔ لنگتون را اتوماتون سلولی با همسایگی فون نویمان دانست. این ماشین همانند بسیاری از دیگر نمونه‌های اتوماتای سلولی مصداقی از یک سیستم پیچیده با قواعد ساده است که بر حسب قواعد می‌تواند رفتاری پیچیده، تصادفی یا ساده داشته باشد. در سال ۲۰۰۰ با اثبات امکان شبیه‌سازی هر مدار دیجیتال دلخواه با مورچهٔ لنگتون، ماشین محاسبهٔ تورینگ بودن این ماشین اثبات شد. افراد مختلفی ایدهٔ مورچهٔ لنگتون را در جهات مختلف گسترش داده‌اند، برای مثال ترمایت‌ها با الگو گرفتن از مورچهٔ لنگتون ابداع شده‌اند که خود گونه‌ای از ماشین محاسبهٔ تورینگ هستند.

ساختار

مورچهٔ لنگتون از یک صفحهٔ شطرنجی دو بعدی نامتنهاهی تشکیل شده‌است که یک مورچه بر روی آن در چهار جهت اصلی حرکت می‌کند. مورچه بر یکی از این خانه‌های صفحه قرار دارد. در هر نوبت، مورچه با توجه به رنگ خانه‌ای که بر روی آن قرار دارد رنگ آن خانه را به رنگ دیگری تغییر می‌دهد و جهت حرکتش را تغییر می‌دهد و یک خانه حرکت می‌کند.

در نمونهٔ اولیه هر خانه می‌تواند یکی از دو رنگ سفید یا سیاه را داشته باشد. مورچه در صورتی که بر خانهٔ سفید قرار داشته باشد ۹۰ درجه به راست می‌چرخد، رنگ خانه را تغییر می‌دهد و به خانهٔ بعدی می‌رود. در صورتی که مورچه بر روی خانهٔ سیاه قرار داشته باشد ۹۰ درجه به چپ می‌چرخد، رنگ خانه را تغییر می‌دهد و به خانهٔ بعدی می‌رود.

می‌توان با گسترش مجموعهٔ رنگ‌ها، یا تغییر دادن قاعدهٔ حرکت مورچه نمونه‌های متعددی از مورچهٔ لنگتون را به دست آورد که هرکدام رفتاری متفاوت با دیگری دارند. در واقع می‌توان صفحهٔ دو بعدی را مشابه نوار حافظهٔ ماشین تورینگ، محل مورچه را سر ماشین تورینگ و قاعدهٔ حرکت مورچه را قاعدهٔ حرکت سر ماشین تورینگ در نظر گرفت. همچنین می‌توان مورچهٔ لنگتون را یک ماشین سلولی در نظر گرفت که در آن، صفحهٔ شطرنجی صفحهٔ ماشین است و به ازای n رنگ در مورچهٔ لنگتون در ماشین سلولی ۵n رنگ وجود دارد. هر خانهٔ خالی در صفحهٔ مورچهٔ یکی از n رنگ را دارد و برای خانهٔ مورچه دار، یکی از 4n رنگ دیگر را انتخاب می‌کنیم که نشان‌دهندهٔ رنگ خانه در مورچهٔ لنگتون، حضور مورچه در آن و جهت‌گیری مورچه است. قوانین تغییر ماشین هم همسایگی فون نویمان هر خانه را در نظر می‌گیرد و آن خانه و همسایگی آن را مشابه قوانین مورچهٔ لنگتون تغییر می‌دهد.

رفتار مورچهلنگتون در جعبه: این نمودار نشان می‌دهد چگونه مورچه به مرور دیوارهٔ جعبه را می‌شکند و به بیرون آن حرکت می‌کند.

رفتار

رفتار یک مورچهٔ لنگتون: در سمت چپ تصویر یک بزرگراه قابل مشاهده است.

در صورتی که مورچه در نمونهٔ اولیه بر صفحه‌ای سفید حرکت خود را شروع کند، ابتدا طرح‌هایی ساده و عموماً متقارن تولید می‌کند، سپس در صفحه الگوهایی پیچیده تصویر می‌کند و در نهایت شروع به ساختن بزرگراه می‌کند که تکرار مداوم ۱۰۴ حرکت مورچه است و در صفحه ساختاری مشابه نوار به وجود می‌آورد.

اثبات می‌شود که در صورتی که شرایط اولیهٔ صفحهٔ مورچهٔ لنگتون متناهی باشد، رفتار مورچه در نهایت به ساخت بزرگراه منتهی می‌شود.

مورچهٔ لنگتون مثالی از یک سیستم پیچیده‌است که قوانینی بسیار ساده دارد و کریس لنگتون به منظور نشان دادن همین مفهوم (امکان بروز رفتار ظهوریافتهٔ پیچیده، حتی در ساده‌ترین ساختارها) ماشین لنگتون را ابداع کرد. انواع مختلف مورچهٔ لنگتون رفتارهای مختلفی از خود نشان می‌دهند که پیچیده، ساده یا تصادفی است. تفاوت این ماشین‌ها در قواعد حرکت مورچه و شرایط اولیهٔ صفحه است.

تصمیم ناپذیری

مورچهٔ لنگتون یک ماشین محاسبه تورینگ است، این مسئله به آن معنی است که رفتار هر ماشین تورینگی را به ازای ورودی مشخص می‌توان با یک ماشین لنگتون شبیه‌سازی کرد. همان‌طور که پیش‌تر ذکر شد، در صورتی که شرایط اولیهٔ صفحهٔ مورچهٔ لنگتون متناهی باشد، رفتار مورچه در نهایت به ساخت بزرگراه منتهی می‌شود. پس رفتار نهایی هر مورچهٔ لنگتون با صفحهٔ اولیهٔ قابل پیش‌بینی است که عبارت است از تکرار کردن یک پترن ۱۰۴ حرکتی مداوم که به اسم بزرگراه شناخته می‌شود. از طرفی اما می‌دانیم که مسئلهٔ رفتار نهایی ماشین تورینگ یا مسئله توقف تصمیم‌ناپذیر است. تصمیم‌ناپذیری این مسئله به آن معنی است که نمی‌توان ماشینی داشت که به ازای هر ماشین تورینگ و هر ورودی w تعیین کند ماشین تورینگ داده‌شده بر روی ورودی w توقف خواهد کرد یا نه.

با توجه به آنچه که گفته شد، ممکن است به نظر برسد که می‌توان مسئله توقف را به مسألهٔ رفتار نهایی مورچهٔ لنگتون کاهش داد و این مسئله تصمیم پذیر است؛ اما این تصور غلط است، چرا که هر ماشین تورینگی به مورچهٔ لنگتونی با شرایط اولیهٔ متناهی کاهش داده نمی‌شود و مسألهٔ تعیین رفتار نهایی مورچهٔ لنگتون در شرایط کلی مسئله‌ای تصمیم ناپذیر است.

مورچهٔ لنگتون در فضای سه‌بعدی

می‌توان برای مورچهٔ لنگتون در فضای سه‌بعدی نیز تعریفی مشابه فضای دو بعدی ارائه داد با این تفاوت که به جای صفحه، فضای سه بعدی محل حرکت مورچه است و مورچه در هر گام به بالا، پایین، چپ یا راست خود حرکت می‌کند. با این تعریف، مورچهٔ لنگتون در فضای سه بعدی نیز رفتاری مشابه با فضای دو بعدی دارد و در بسیاری از اوقات در نهایت شروع به ساختن بزرگراه می‌کند که حرکتی تناوبی با دورهٔ تناوب ۱۰۴ گام است. همچنین می‌توان برای فضاهای n بعدی نیز تعریفی مشابه برای مورچهٔ لنگتون ارائه داد.

انواع مختلف

می‌توان انواع مختلفی از مورچهٔ لنگتون را با تغییر دادن شرایط اولیهٔ صفحه و تعداد رنگ‌ها به وجود آورد. منطق پشت حرکت مورچه را می‌توان با رشته‌ای از R و L نمایش داد که مشخص می‌کند به ازای هر رنگ مورچه به کدام سمت حرکت می‌کند. با این شیوه مورچهٔ لنگتون اولیه را می‌توان با RL نمایش داد. برخی از این مورچه‌ها در گذر زمان ساختاری متقارن می‌سازند، برای مثال مورچه‌هایی که در قاعدهٔ خود LL یا RR داشته باشند ساختارهای متقارنی را به وجود خواهند آورد. تصاویر زیر چند نمونه از رفتار این‌گونه مورچه‌هاست.

• 
• 
• 
• 

می‌توان به مورچهٔ لنگتون چند وضعیت متفاوت اضافه کرد و گونه‌ای از ترمایت‌ها را تولید کرد. رفتار چند ترمایت از این دست در اشکال زیر قابل مشاهده است.

• 
• 
• 
• 
• 

چند مورچهٔ لنگتون با رنگ‌های متفاوت

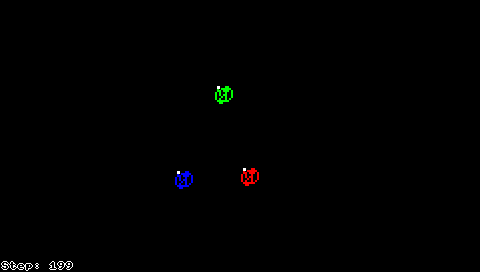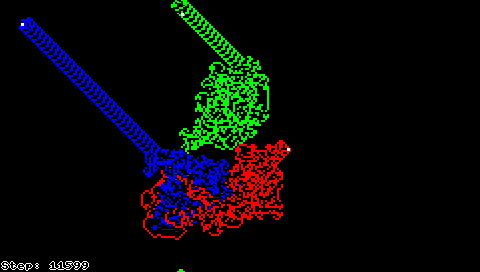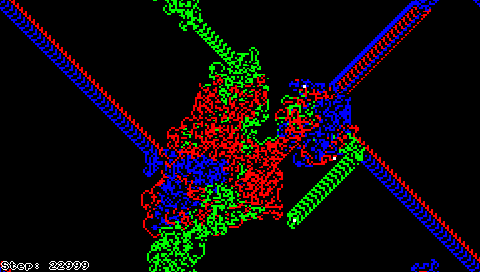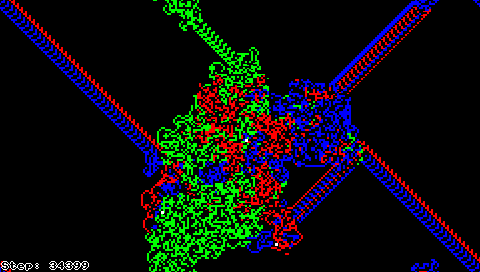
گونهٔ دیگری از مورچهٔ لنگتون با قرار دادن چندین مورچه بر روی صفحه ساخته می‌شود. این مورچه‌ها می‌توانند از قواعد یکسان یا متفاوتی پیروی کنند که در صورتی که قواعد حرکت مورچه‌ها با یکدیگر متفاوت باشد باید از شرایطی که دو مورچه بر یک خانه قرار دارند با تعیین سرنوشت رنگ خانه رفع ابهام کرد.

با افزایش تعداد رنگ‌ها می‌توان نمونه‌هایی مشابه تصویر مقابل به دست آورد: همچنین به جای صفحه، می‌توان فضایی n بعدی در نظر گرفت که خانه‌های همسایه در آن خانه‌هایی هستند که تنها یک درایهٔ آن‌ها به خانهٔ اولیه متفاوت است. در فضای سه بعدی نیز مورچه‌ها برای شرایط اولیهٔ متنهای در نهایت شروع به ساختن بزرگراه‌های با دوره تناوب ۱۰۴ قدم می‌کنند.