جستجوی مینیمم بازهای

در علوم کامپیوتر، یک جستجوی میبنیمم بازهای (Range minimum query) الگوریتمی برای یافتن کوچکترین عنصر در یک زیر آرایه (بازهای از یک آرایه) با عناصر قابل مقایسه است.
الگوریتم جستجوی مینیمم بازهای در علوم و مهندسی کامپیوتر کاربردهای فراوانی دارند. از جمله آنان میتوان به یافتن پایینترین والد مشترک (مثلا در درخت یا هرم یا …) یا طولانیترین پیشوند مشترک (LCP) اشاره کرد. (لینک خارجی LCP array)
تعریف
[ویرایش]با توجه به یک آرایه [A[1 … n از n اشیاء از یک مجموعه منظم(خوش ترتیب) (مانند اعداد)، جستجوی مینیمم بازهای [RMQ A(l,r) =arg min A[k (با ۱ ≤ l ≤ k ≤ r ≤ n ) موقعیت(اندیس ) کوچکترین عنصر را در زیربازهی مشخص شده [A[l … r بازمیگرداند.
به عنوان مثال ، وقتی A = [۰٬۵٬۲٬۵٬۴٬۳٬۱٬۶٬۳]، آنگاه پاسخ به سؤال از دامنه A[۳ … ۸] = [۲٬۵٬۴٬۳٬۱٬۶] برای زیر مجموعه A برابر است با ۷. زیرا A[7] = ۱. و پاسخ، موقعیت کوچکترین عنصر در زیربازهٔ مشخص شده را به ما میدهد. (البته اینجا اندیسها را برای سادگی از یک شروع کردیم. اما در واقعیت از ۰ آغاز میشوند)
الگوریتمها
[ویرایش]راه حل بدیهی
[ویرایش]در یک مجموعه رایج، آرایه A استاتیک است، یعنی عناصر در طی یک سری پرس و جوها درج یا حذف نمیشوند؛ و جستجوهای داده شده باید به صورت درجا پاسخ داده شوند (یعنی کل مجموعه نمایش دادهها از قبل با الگوریتم مشخص نیست) در این حالت، پیش پردازش مناسب آرایه در یک داده ساختار، پاسخ سریع تر پرس و جو را تضمین میکند. یک راه حل ساده این است که پاسخ تمام جستجوهای ممکن را از قبل حساب کنیم، یعنی مینیمم تمام زیر مجموعههای A، و این موارد را در یک آرایه B ذخیره کنید به طوری که [B[i, j] = min(A[i…j) ؛ سپس با استفاده از جستجوی آرایه در B یک جستجوی مینیمم در زمان ثابت حل میشود. تعداد (Θ(n² جستجوی مختلف روی آرایهای به طول n وجود دارد، و پاسخ به این سوالات را میتوان در زمان (Θ(n² توسط برنامهنویسی پویا بدست آورد.
راه حل با استفاده از زمان ثابت و حافظه خطی
[ویرایش]| k | |||||
|---|---|---|---|---|---|
| ۰ | ۱ | ۲ | ۳ | ||
| l | ۱ | ۱ | ۱ | ۱ | ۱ |
| ۲ | ۲ | ۳ | ۳ | ۷ | |
| ۳ | ۳ | ۳ | ۳ | ۷ | |
| ۴ | ۴ | ۵ | ۶ | ۷ | |
| ۵ | ۵ | ۶ | ۷ | ۷ | |
| ۶ | ۶ | ۷ | ۷ | ۷ | |
| ۷ | ۷ | ۷ | ۷ | ۷ | |
| ۸ | ۸ | ۷ | ۷ | ۷ | |
| ۹ | ۹ | ۷ | ۷ | ۷ | |
مانند راه حل بالا، پاسخ دادن به این سؤالات در زمان ثابت با نتایج از پیش محاسباتی حاصل میشود. با این حال، این آرایه جستجوهای مینیمم از پیش محاسبه شده را برای محدودههایی که اندازه آنها توانی از ۲ است برای همه عناصر ذخیره میکند. برای هر موقعیت شروع i به تعداد (Θ(log n از این جستجوها وجود دارد، بنابراین اندازه جدول برنامهنویسی پویا B برابر با (Θ (n log n است. هر عنصر [B [i, j دارای اندیس مینیمم محدوده [A [i … i + 2^j-1 است. جدول به کمک خاصیت بازگشت از اندیسهای مینیممها پر شدهاست.
اگر A[B[i, j-1]] ≤ A[B[i+2j-1, j-1]]،
آن گاه B[i, j] = B[i, j-1].
در غیر این صورت، B[i, j] = B[i+2j-1, j-1].
اکنون با تقسیم آن به دو پرس و جو جداگانه میتوان به پرس و جو (RMQ A(l,r پاسخ داد: یکی پرس و جو از پیش محاسبه شده با دامنه از l تا بالاترین مرز کوچکتر از r (که طول این بازه توانی از ۲ است). مورد دیگر عبارت است از یک بازه با همان طول که r آن را به عنوان مرز سمت راست خود دارد. این فواصل ممکن است با هم هم پوشانی داشته باشند، اما با توجه به اینکه مینیمم به جای جمع، محاسبه میشود، این مهم نیست. نتیجه کلی را میتوان در زمان ثابت بدست آورد زیرا میتوان به این دو پرس و جو در زمان ثابت پاسخ داد و تنها کاری که باقی ماندهاست ، انتخاب عنصر کوچکتر بین دو عنصر جواب این دو نتیجه است. (که حتی ممکن است یکی باشند)
راه حل با استفاده از زمان لگاریتمی و حافظه خطی
[ویرایش]این راه حل RMQ را در (O(log n پاسخ میدهد. داده ساختار آن حافظهای از مرتبهٔ (O(n میگیرد و از این داده ساختار نیز میتوان برای پاسخ به جستجوها در زمان ثابت استفاده کرد. این آرایه ابتدا از نظر مفهومی به بلوکهایی با اندازه تقسیم میشود. سپس عنصر مینیمم برای هر بلوک در (O(n محاسبه میشود و مینیممها در یک آرایه جدید ذخیره میشوند.
اکنون RMQها را میتوان با مراجعه به بلوکهای حاوی مرز سمت چپ و راست بازه داده شده در طرفین، و تمام بلوکهای موجود در زمان لگاریتمی پاسخ دهید:
دو بلوک حاوی مرزها را میتوان به سادگی جستجو کرد. عناصر خارج از مرز حتی لازم نیست مورد بررسی قرار گیرند. این کار در زمان لگاریتمی قابل انجام است.
مینیمم تمام بلوکهایی که بهطور کامل در محدوده موجود است و دو مینیمم ذکر شده در بالا، برای پاسخ به پرس و جو باید مقایسه شوند. از آنجا که آرایه به بلوکهایی با اندازه تقسیم شدهاست، حداکثر بلوک وجود خواهند داشت که کاملاً در داخل محدوده قرار دارند.
با استفاده از راه حل خطی میتوان مینیمم کلی را در بین این بلوکها پیدا کرد. این داده ساختار دارای اندازه (O( * log()) است.
به عنوان مثال، با استفاده از آرایه [A = [۰٬۵٬۲٬۵٬۴٬۳٬۱٬۶٬۳ و اندازه بلوک ۳ (فقط برای اهداف مصور) آرایه مینیمم [A' = [۰٬۳٬۱ را برمیگرداند.
راه حل با استفاده از زمان ثابت و حافظه خطی
[ویرایش]با استفاده از راه حل فوق ، زیر محدودههای داخل بلوکهایی که بهطور کامل در آن محدوده قرار ندارند ، هنوز هم باید در زمان ثابت پاسخ داده شوند. حداکثر دو بلوک وجود دارد: بلوک حاوی l و بلوک حاوی r . با نگه داشتن درختان دکارتی برای تمام بلوکهای موجود در آرایه ، زمان ثابت حاصل میشود. تعدادی از مشاهدات:
- بلوکهای دارای درختان ایزومورفیک یا یکریخت دکارتی نتیجه یکسان را برای همه جستجوهای موجود در آن بلوک میدهند.
- تعداد درختان مختلف دکارتی از s گره برابر است با Cs که s'امین عدد کاتالان است.
- بنابراین، تعداد درختان مختلف دکارتی برای بلوکها در محدوده 4s قرار دارد.
برای هر درخت این چنینی، نتیجه احتمالی برای همه سؤالات باید ذخیره شود. این به ورودیهای از مرتبه s2 یا O (log2 n) بستگی دارد. این بدان معنی است که اندازه کلی جدول (O(n است.
برای جستجوی بهینهٔ نتایج، درخت دکارتی (ردیف) مربوط به یک بلوک خاص باید در زمان ثابت مورد قرار گیرد. راه حل این است که نتایج را برای کلیه درختان در یک آرایه ذخیره کرده و یک تصویرسازی و طرحریزی منحصر به فرد از درختان باینری به اعداد صحیح برای آدرس دهی پیدا کنید. این کار را میتوان با انجام یک پیمایش درخت روی درخت و اضافه کردن گرههای برگ بدست آورد به طوری که هر گره موجود در درخت دکارتی دقیقاً دو فرزند داشته باشد. سپس عدد صحیح با به نمایش گذاشتن هر گره درونی به عنوان یک بیت ۰ و هر برگ به عنوان بیت ۱ در یک بیت کلمه (با عبور دوباره درخت به صورت سطح به سطج) ایجاد میشود. این برای هر درخت به اندازه منجر میشود. برای فعال کردن دسترسی تصادفی در زمان ثابت به هر درخت، درختانی که در آرایه اصلی موجود نیستند نیز باید در آرایه درج شوند. آرایهای با شاخصهای به طول بیت، اندازهای از مرتبهٔ 2 دارند.
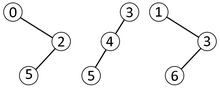
| Index | 1 | 2 | ۳ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ۱ | ۲ | ۳ | ۱ | ۲ | ۳ | ۱ | ۲ | ۳ | |
| 0 | — | ||||||||
| 23 (Bitword 0010111) | 1 | 2 | 3 | — | 2 | 3 | — | — | ۳ |
| 39 (Bitword 0100111) | 1 | 1 | 1 | — | 2 | 3 | — | — | ۳ |
| 127 | — | ||||||||
کاربردها
[ویرایش]RMQها به عنوان ابزاری برای بسیاری از کارها در تطابق دقیق و تقریبی رشته استفاده میشوند. چندین کاربرد را میتوان در مقالههای فیشر و هون (۲۰۰۷) یافت.[۱] : 3
محاسبه پایینترین جد مشترک در یک درخت
[ویرایش]RMQها میتوانند برای حل مسئله پایینترین جد مشترک[۲] استفاده شوند و به عنوان ابزاری برای بسیاری از کارها در تطابق دقیق و تقریبی رشته استفاده میشوند. query LCAS(v, w) از یک درخت ریشه دار S = (V, E) و دو گره v, w ∈ V عمیقترین گره u (که ممکن است v یا w باشد) را در مسیرهای ریشه به هر دو w بازمیگرداند؛ و v گابوو ، بنتلی و تارجان (۱۹۸۴) نشان دادند که مسئله LCA میتواند در زمان خطی به مسئله RMQ تقلیل یابد. از این رو نتیجه میگیرد که مانند مسئله RMQ، مسئله LCA میتواند در زمان ثابت و حافظهٔ خطی حل شود.[۱]
الگوریتم جستجوی مینیمم بازهای در علوم و مهندسی کامپیوتر کاربردهای فراوانی دارند. از جمله آنان میتوان به یافتن پایینترین والد مشترک (مثلا در درخت یا هرم یا …) یا طولانیترین پیشوند مشترک (LCP) اشاره کرد.
محاسبه طولانیترین پیشوند مشترک در یک رشته
[ویرایش]این مفهوم در برنامههای بسیاری بکار میرود.
در زمینه نمایه سازی متن، از RMQها میتوان برای یافتن LCP (طولانیترین پیشوند مشترک) استفاده کرد، جایی که LCPT(i, j) LCP پسوندهایی را که در شاخصهای i و j در T شروع میشود LCPT(i, j) محاسبه میکند. برای این کار ابتدا آرایه پسوند A و آرایه پسوند معکوس A−1 را محاسبه میکنیم. سپس LCP آرایه H را به کمک LCP پسوندهای مجاور در A محاسبه میکنیم. پس از محاسبه این ساختارهای داده، و پردازش RMQ کامل میشود، طول LCP عمومی را میتوان در زمان ثابت با فرمول محاسبه کرد: LCP(i, j) = RMQH(A-1[i] + 1, A-1[j])، جایی که ما برای سادگی فرض میکنیم که A-1[i] + 1 <= A-1[j] (در غیر این صورت مبادله میکنیم).[۳]
جستارهای وابسته
[ویرایش]انگلیسی
[ویرایش]- یافتن نزدیکترین عناصر کوچکتر
- برنامهنویسی پویا
- پیمایش درخت
- جستجوی بازهای (داده ساختار)
- بیشینه و کمینه
فارسی
[ویرایش]منابع
[ویرایش]- Berkman, Omer; Vishkin, Uzi (1993). "Recursive Star-Tree Parallel Data Structure". SIAM Journal on Computing. 22 (2): 221–242. doi:10.1137/0222017.
- Johannes Fischer. Optimal Succinctness for Range Minimum Queries (Report).
- ↑ ۱٫۰ ۱٫۱ Fischer, Johannes; Heun, Volker (2007). A New Succinct Representation of RMQ-Information and Improvements in the Enhanced Suffix Array. Proceedings of the International Symposium on Combinatorics, Algorithms, Probabilistic and Experimental Methodologies. LNCS. 4614. Springer. pp. 459–470. doi:10.1007/978-3-540-74450-4_41.
- ↑ Bender, Michael A.; Farach-Colton, Martín; Pemmasani, Giridhar; Skiena, Steven; Sumazin, Pavel (2005). "Lowest common ancestors in trees and directed acyclic graphs" (PDF). Journal of Algorithms. 57 (2): 75–94. doi:10.1016/j.jalgor.2005.08.001.
- ↑ Fischer, J. and V. Heun (2006). Theoretical and practical improvements on the RMQ-problem, with applications to LCA and LCE. Combinatorial Pattern Matching. Lecture Notes in Computer Science. Vol. 4009. pp. 36–48. doi:10.1007/11780441_5. ISBN 978-3-540-35455-0.
- ↑ Fischer, Johannes; Heun, Volker (2007). A New Succinct Representation of RMQ-Information and Improvements in the Enhanced Suffix Array. Proceedings of the International Symposium on Combinatorics, Algorithms, Probabilistic and Experimental Methodologies. LNCS. 4614. Springer. pp. 459–470. doi:10.1007/978-3-540-74450-4_41.





