الگوریتم ای استار
| رده | الگوریتم جستجو |
|---|---|
| ساختمان داده | گراف (ساختار داده) |
| کارایی بدترین حالت | |
| پیچیدگی فضایی |
در علوم کامپیوتر، الگوریتم A* یک الگوریتم مسیریابی است که برای پیمایش و یافتن مسیر در گراف استفاده میشود. به علت کامل بودن، بهینه بودن (یافتن جواب بهینه) و سرعت مناسب این الگوریتم، استفاده گستردهای از آن میشود. مشکل اصلی این الگوریتم استفادهٔ زیاد از حافظه است که باعث میشود در بسیاری از مسائل عملی ضعیف تر از سایر الگوریتمها عمل کند. پیتر ای هارت (به انگلیسی: Peter E. Hart)، نیلز نیلسون (Nils Nilsson) و برترام رافائل (Bertram Raphael) اولین کسانی بودند که آن را در سال ۱۹۶۸ میلادی شرح دادند. این الگوریتم در واقع تعمیمی از الگوریتم دیکسترا میباشد که با استفاده از روشهای فرا ابتکاری عملکرد بهتری در زمینه جستجو بدست آوردهاست.
تاریخچه[ویرایش]

الگوریتم A* به عنوان بخشی از پروژه [[[:en:Shakey the robot|ربات شیکی]]] ساخته شد. هدف این پروژه ساخت یک ربات متحرک بود که بتواند کاریهای خودش را برنامهریزی کند. نیلز نیلسون الگوریتم پیماینده گراف را برای برنامهریزی حرکت شیکی معرفی کرد. این الگوریتم از یک تابع هیوریستیک به نام استفاده میکند که تخمین فاصله گره تا هدف است. در این الگوریتم اصلاً از تابع که فاصله گره شروع تا را نشان میدهد استفادهای نمیشود. برترام رافائل پیشنهاد استفاده از جمع هر دو این توابع را داد (). پیتر هارت مفاهیمی که امروزه با نامهای قابل قبول و یکپارچه شناخته میشوند را ابداع کرد. در ابتدا A* برای پیدا کردن مسیر با کمترین هزینه (هزینه مسیر، جمع هزینههای یالهایش است) طراحی شده بود. اما امروزه مشخص شده که از این الگوریتم میتواند برای پیدا کردن مسیر بهینه در تمامی مسائلی که شروط Cost-Algebraic[۱] را دارند، استفاده شود.
توضیح[ویرایش]

A* یک [[[:en:Search algorithm#Informed search|جستجوی آگاه]]]، یا یک جستجوی ابتدا بهترین است، که یعنی از یک گره مشخص (گره شروع) جستجو را آغاز میکند و هدفش پیدا کردن یک مسیر به گره نهایی یا هدف است که کمترین هزینه را دارد. این روش با ترکیب هزینه رسیدن به گره و هیوریستیک یا تخمین هزینه رسیدن از گره م تا هدف گرهها را ارزیابی میکند:
از آنجایی که هزینه مسیر از گره شروع به گره و هزینه تخمینی ارزانترین مسیر از به هدف است، داریم:
بنابراین اگر به دنبال ارزانترین راه حل هستیم، اولین کار معقول امتحان گرهای است که کمترین مقدار را داراست. مشخص میشود که این راهبرد کاملاً معقولانهاست. اگر تابع آروین قابل قبول و جستجو درختی باشد الگوریتم بهینه است. اما اگر جستجوی گراف باشد علاوه برای قابل قبول بودن لازم است تا یکپارچه نیز باشد.
اگر A* همراه با الگوریتم جستجوی درخت استفاده شود، آنگاه تحلیل بهینگی آن بسیار ساده و سر راست میشود. A* بهینهاست اگر یک آروین قابل قبول باشد؛ یعنی هرگز هزینه رسیدن به هدف را بیش از اندازه واقعی برآورد نکند. این آروینها ذاتاً بهینه هستند زیرا آنها فکر میکنند که هزینه راه حل مسئله کمتر از مقدار واقعی آن است. از آنجا که هزینه رسیدن به را بهطور دقیق نشان میدهد، میتوان بلافاصله نتیجه گرفت که هرگز هزینه واقعی راه حلی که از میگذرد را اضافه برآورد نمیکند.
پیادهسازی معمول A* از یک صف اولویتدار استفاده میکند تا گرههای دارای کمترین هزینه برآورد شده را در هر مرحله برای باز کردن انتخاب کند. در هر مرحله، گره با کمترین از صف حذف میشود، سپس تابع همسایههای آن گره به روز رسانی میشود و در نهایت همسایهها به صف اضافه میشوند. جستجو زمانی به پایان میرسد که یا مسیری از گره شروع به هدف یافت نمیشود، به عبارت دیگر صف خالی میشود و دیگری گرهای برای باز کردن وجود ندارد. یا به گره هدف میرسد که در این صورت مقدار همان کمترین هزینه است برای رسیدن به گره هدف، زیرا تابع در هدف به علت قابل قبول بودن ۰ است.
شبه کد[ویرایش]
شبه کد زیر الگوریتم را توصیف میکند:
function A*(start,goal)
closedset:= the empty set // The set of nodes already evaluated.
openset:= {start} // The set of tentative nodes to be evaluated,
// initially containing the start node
came_from:= the empty map // The map of navigated nodes.
g_score[start]:= 0 // Cost from start along best known path.
h_score[start]:= heuristic_cost_estimate(start, goal)
f_score[start]:= g_score[start] + h_score[start] // Estimated total cost
// from start to goal through y.
while openset is not empty
x:= the node in openset having the lowest f_score[] value
if x = goal
return reconstruct_path(came_from, came_from[goal])
remove x from openset
add x to closedset
foreach y in neighbor_nodes(x)
if y in closedset
continue
tentative_g_score:= g_score[x] + dist_between(x,y)
if y not in openset
add y to openset
tentative_is_better:= true
else if tentative_g_score <g_score[y]
tentative_is_better:= true
else
tentative_is_better:= false
if tentative_is_better = true
came_from[y]:= x
g_score[y]:= tentative_g_score
h_score[y]:= heuristic_cost_estimate(y, goal)
f_score[y]:= g_score[y] + h_score[y]
return failure
function reconstruct_path(came_from, current_node)
if came_from[current_node] is set
p:= reconstruct_path(came_from, came_from[current_node])
return (p + current_node)
else
return current_node
نکات پیادهسازی[ویرایش]
کارهای زیادی برای بهبود عملکرد این الگوریتم میتوان انجام داد. یکی از این کارها نحوهٔ انتخاب گرههای با هزینههای یکسان از صف اولویت است. اگر در شرایط تساوی چند گره، پیادهسازی به نحوی باشد که آخرین گره ورودی اولین گره خروجی باشد (LIFO)، الگوریتم مشابه جستجو عمق اول عمل میکند و از جستجوی مسیرهای بهینه با هزینه یکسان جلوگیری میکند.
اگر به جز هزینه کمینه خود مسیر هم مورد سؤال باشد، لازم است که در هر گره یک اشارهگر به پدر آن گره وجود داشته باشد که با پایان جستجو بتوان مسیر را با دنبال کردن اشارهگرها یافت. اما در این حالت باید از حضور چند نمونه از یک گره در صف جلوگیری شود. یک روش این است که اگر گره خواست به صف اضافه شود ولی در صف حضور داشت، به جای اضافهکردن مجدد آن، اشارهگر پدر و هزینهٔ گره موجود در صف، بروزرسانی گردد. این کار توسط صفهایی که بر اساس هرم دودویی ساخته شدهاند به تنهایی ممکن نیست ولی میتوان با کمک گرفتن از جدول درهمسازی برای ذخیره مکان گره در هرم بروزرسانی را انجام داد. همچنین روشهای دیگری مثل استفاده از هرم فیبوناچی برای ساخت صف اولویت نیز قابل استفاده هستند.
مثال[ویرایش]

یک مثال از الگوریتم A* در عمل این است که گرهها را شهرهایی فرض کنیم که با جادههایی به هم وصل شدهاند و فاصله اقلیدسی نقطهٔ x تا نقطه هدف باشد:
کلید: سبز:شروع؛ آبی: هدف؛ نارنجی: گره ملاقات شده.
مثالی دیگر برای A* مسئله n-puzzle است که در آن هدف مرتبسازی پازل است به نحوی که اعداد به ترتیب مرتب شوند. برای این مسئله یک تابع هیوریستیک نسبتاً ساده میتواند تعداد خانههایی باشد که در مکان اشتباه قرار دارند. همچنین g تعداد حرکتهایی میشود که تا حالا انجام شدهاست.
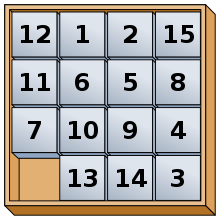
در چند مثال زیر تأثیر تابع هیوریستیک در پیدا کردن مسیر بهینه قابل مشاهده است.




کلید: سبز پر رنگ:شروع -- قرمز: هدف -- آبی: خانههای دیده شده -- سبز کم رنگ: خانههای همسایه.
خصوصیات[ویرایش]
خاتمه و کامل بودن[ویرایش]
در گرافهایی که محدود هستند و یالهایشان وزن نامنفی دارند الگوریتم A* کامل است و خاتمه مییابد، یعنی اگه مسیری از گره شروع به هدف موجود باشد این الگوریتم آن را پیدا میکند. اگر گراف نامحدود باشد تنها در صورتی که یک جواب موجود باشد و برای تمامی یالها یک حد پایین برای وزن موجود باشد مثل ()، تضمین میشود که الگوریتم خاتمه بیابد.
قابل قبول بودن[ویرایش]
یک الگوریتم جستجو قابل قبول است اگر تضمین شود که یک جواب بهینه پیدا میکند. در الگوریتم A* اگر تابع قابل قبول باشد الگوریتم قابل قبول است. یک اثبات شهودی برای این مسئله به صورت زیر است:
وقتی جستجو به پایان میرسد، الگوریتم یک جواب پیدا کردهاست که هزینهاش از تمام مسیرهای دیگر کمتر مساوی است. وقتی هیوریستیک قابل قبول است یعنی یک حد پایینی از مقدار واقعی را دارد پس برای هر مسیر مقدارش کمتر از مقدار واقعی نیست و A* آن مسیرهایی را که کمینه نیستند را در نظر نمیگیرد. با این کار امکان ندارد که مسیری در نظر گرفته نشود اگر هزینه کمتری داشته باشد.
بهرهوری بهینه (Optimal efficiency)[ویرایش]
یک الگوریتم Optimal efficient است اگر به ازای هر مسئله در یک مجموعه از مسائل و هر الگوریتم در یک مجموعه از الگوریتمهای جایگزین، گرههایی که باز میکند یک زیرمجموعه از گرههایی باشد که الگوریتم جایگزین باز میکند. بررسی کامل optimal efficiency الگوریتم A* توسط رینا دچر (Rina Dechter) و جودیا پرل (Judea Pearl) انجام شدهاست[۲]. ولی یک اثبات نسبتاً کوتاه از این موضوع به شرح زیر است:
اگر هزینهٔ کوتاهترین مسیر به هدف باشد و یک الگوریتم دیگر باشد که شروعش با یکی بودهاست و هیوریستیکش هم یکی باشد و بهینه هم باشد (همواره مسیر بهینه را پیدا کند). در این مسئله مسیری مثل را که توسط باز شده را باز نمیکند. () حال اگر یک مسئله دیگر باشد دقیقاً مشابه این مسئله با این تفاوت که یک فرزند دارد که خود هدف است و مثلاً نامش است. در این حالت خود هزینه است و هیوریستیک دقیق است. در این مسئله ، مسیر را باز نمیکند؛ یعنی جوابی که در نهایت پیدا میکند بیشتر از هزینه میشود که این متناقض با بهینه بودن است. درنتیجه یک الگوریتم optimally efficient است.
پیچیدگی[ویرایش]
پیچیدگی زمانی[ویرایش]
پیچیدگی زمانی الگوریتم A* به تابع هیوریستیک آن بستگی دارد. در بدترین حالت، تعداد گرههای فضای جستجوی درون تراز هدف، نسبت به طول راه حل، نمایی میباشد. O(bd) که در این رابطه ضریب انشعاب میباشد و عمق جواب بهینه میباشد.
تعداد گرههایی که در الگوریتم باز میشود به صورت زیر است:
که در این رابطه ضریب انشعاب مؤثر است. هر چه هیوریستیک بهتر باشد این ضریب کمتر است و پیچیدگی زمانی بهتر.
در صورتی که محیط جستجو درخت باشد و یک گره هدف وجود داشتهباشد و خطای تابع آروین سریع تر از لگاریتم هزینه واقعی رشد نکند (عبارت ریاضی در پایین آمدهاست)، پیچیدگی زمانی چندجملهای خواهد بود:
که در آن هزینه واقعی رسیدن از گره به هدف است.
پیچیدگی فضایی[ویرایش]
پیچیدگی فضایی الگوریتم A* تقریباً برابر با سایر الگوریتمهای جستجوی گراف است زیرا تمام گرههای باز شده را در حافظه نگهمیدارد. از این رو زمان محاسبه، نقطه ضعف اصلی A* نیست و معمولاً بیشتر از آنکه وقت کم بیاورد، حافظه کم میآورد. به همین دلیل A* در مورد بسیاری از مسائل بزرگ، عملی نیست و جایگزینهای بهتری مثل [[[:en:Iterative deepening A*|IDA*]]] برایش آمدهاند.
انواع[ویرایش]

در طول سالها انواع مختلفی از A* معرفی شدهاست که چند مورد آن به شرح زیر است:
همچنین میتوان از A* به صورت یک الگوریتم جستجوی دوجهته استفاده کرد که البته نیاز به کمی تغییرات دارد.
ارتباط با سایر الگوریتمها[ویرایش]
الگوریتم A* چیزی بین الگوریتم حریصانه و الگوریتم دکسترا است. از نظر در نظر گرفتن شبیه به الگوریتم حریصانه است در واقع اگر در A* صفر باشد یک الگوریتم حریصانه میشود. از نظر در نظر گرفتن شبیه به الگوریتم دکسترا است در واقع اگر در A* صفر باشد مشابه دکسترا عمل میکند.
از طرفی الگوریتم A* خود یک نمونه از برنامهنویسی پویا است.
کاربردها[ویرایش]
الگوریتم A* در مسائل مسیریابی در بازیهای کامپیوتری کاربرد گستردهای دارد. همچنین در برنامهریزی عصبی زبانی (NLP)، گرامر مستقل از متن تصادفی (PCFG) و مطالبی از این دست نیز کاربرد دارد.
منابع[ویرایش]
مشارکتکنندگان ویکیپدیا. «A* search algorithm». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۸ مهٔ ۲۰۱۹.
- ↑ Edelkamp, Stefan; Jabbar, Shahid; Lluch-Lafuente, Alberto (2005). "Cost-Algebraic Heuristic Search" (PDF). Proceedings of the Twentieth National Conference on Artificial Intelligence (AAAI): 1362–1367.
- ↑ Dechter, Rina; Judea Pearl (1985). "Generalized best-first search strategies and the optimality of A*". Journal of the ACM. 32 (3): 505–536. doi:10.1145/3828.3830.
کتاب هوش مصنوعی: رهیافتی نوین – نوشته استوارت راسل و پیتر نورویگ – ترجمه سعید راحتی، چاپ سیزدهم. مشهد: دانشگاه امام رضا (ع)، ۱۳۸۹ ۹۷۸-۶۰۰-۵۶۵۰-۰۶-۸.
https://web.archive.org/web/20200413111416/http://qiao.github.io/PathFinding.js/visual/




























