مربع جادویی

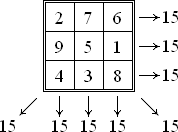
مربع جادویی جدولی ریاضی متشکل از n×n خانه است که خانه‌های آن با اعداد صحیح مثبت از ۱ تا n² چنان پر شده که مجموع اعداد هر ردیف افقی، هر ستون عمودی و هر دو قطر اصلی آن، عددی ثابت است. شکل رایج آن شامل اعداد ۱ تا n² است، اما گاه به‌جای عدد از حرف یا واژه نیز استفاده شده است.

در سنت علوم خفیه و نجوم احکامی، مربع جادویی با نام وفق یا علم اوفاق شناخته می‌شده و به آن خواص فراطبیعی نسبت داده می‌شده است. این نسبت‌ها جنبهٔ اعتقادی و تاریخی دارند و از نظر علمی تأییدنشده و در ردهٔ شبه‌علم قرار می‌گیرند. بنا بر باورهای رایج در سنت اوفاق، هنگامی که مجموع سطرها و ستون‌ها و قطرهای جدول با هم برابر شود، آن را «موفق» می‌خوانند و ادعا شده است که در پی این تنظیم، «انرژی‌های نهفته» در متن واژه‌ها (آیات، اذکار، عزائم و…) که به عدد برگردانده شده‌اند، متمرکز شده و در «عالم مثال» اثر می‌گذارند. چنین ادعاهایی مبنای علمی ندارند.

فرمول ثابت جادویی

عدد ثابتی که مجموع هر سطر، ستون و قطر با آن برابر است، «ثابت جادویی» یا «جمع جادویی» نامیده می‌شود و از رابطهٔ زیر به‌دست می‌آید:

n(n²+۱)/۲

برای نمونه، ثابت جادویی برای n برابر ۳، ۴، ۵ و ۶ به‌ترتیب برابر است با:

۱۵، ۳۴، ۶۵، ۱۱۱

مربع جادویی ۳×۳ و مربع‌های بزرگ‌تر جواب یکتا ندارند؛ برای مثال مربع جادویی ۳×۳ (بدون در نظر گرفتن دوران و بازتاب یک جواب پایه) هشت حالت دارد.

مربع جادویی برای هر n بزرگ‌تر از ۲ ساخت‌پذیر است؛ این مسئله برای n=۲ جواب ندارد و کوچک‌ترین مربع جادویی غیربدیهی، مربع ۳×۳ است.

نام‌گذاری در سنت اوفاق

بنا بر منابع اوفاق، چون مجموع عددی سطرهای افقی و عمودی هر شکل باید ثابت باشد، به همهٔ آن‌ها نام «مربع» داده شده و سپس تعداد خانه‌ها و توضیح شکل نیز افزوده می‌شده تا کد شکل کامل شود. برای نمونه گفته می‌شده «مربع چهار در چهار خماسی»، یعنی شکلی با شانزده خانه که هر خانهٔ آن از پنج خانه ترکیب شده و موفق است.

تاریخچه و مفهوم فرهنگی

مربع جادویی قرن‌ها برای انسان جذاب بوده و بیش از ۴۰۰۰ سال است که در فرهنگ‌های گوناگون از جمله هند، ایران، چین و اروپا دیده شده، بیشتر به‌صورت حکاکی روی سنگ یا فلز.

در برخی فرهنگ‌ها بر این باور بوده‌اند که مربع جادویی پایه‌های نجومی و پیش‌گویانه دارد و برخی پیش‌گویان از آن برای مقاصدی چون تعیین طول عمر یا دفع بیماری بهره می‌برده‌اند. این کاربردها اعتقادی بوده و اعتبار علمی ندارند.

در بین ایرانیان

تاریخ دقیق استفاده از مربع جادویی در ایران روشن نیست، اما برخی بر این گمان‌اند که ایرانیان پیش از اسلام نیز با آن آشنا بوده‌اند. کاربرد مربع جادویی در دورهٔ اسلامی در ایران رواج داشته است. ریاضیدان ایرانی بوزجانی در آثار خود شمار زیادی مربع جادویی و شیوهٔ ساخت آن‌ها را ثبت کرده است.

در بین اعراب

مربع‌های جادویی برای ریاضیدانان مسلمان و عرب نیز شناخته‌شده بودند و به‌نظر می‌رسد این آشنایی از راه تماس با هند به‌دست آمده باشد. از نخستین نمونه‌ها در متون عربی می‌توان به کتاب رسائل اخوان‌الصفا اشاره کرد. احمد بونی در کتاب شمس المعارف الکبری دربارهٔ مربع‌های جادویی بحث کرده و به هریک خواص سحرآمیزی نسبت داده است؛ این نسبت‌ها بخشی از سنت خفیه‌اند و تأییدی علمی ندارند.

مربع جادویی در کتاب شمس المعارف

در هندوستان

مربع‌های جادویی در برخی آیین‌های هندوان کاربرد داشته‌اند. برای نمونه مربع ۳×۳ای به نام Kubera-Kolam روی زمین کشیده می‌شده که همان مربع جادویی درجهٔ ۳ است، با این تفاوت که به هر خانه ۱۹ واحد افزوده شده و ثابت جادویی آن ۷۲ می‌شود:

۲۳	۲۸	۲۱
۲۲	۲۴	۲۶
۲۷	۲۰	۲۵

مربع جادویی شناخته‌شده‌ای در معبد Parshvanath Jain وجود دارد:

۷	۱۲	۱	۱۴
۲	۱۳	۸	۱۱
۱۶	۳	۱۰	۵
۹	۶	۱۵	۴

عدد جادویی این مربع ۳۴ است و بنا بر منابع، در سدهٔ دهم میلادی روی دیوار معبد حکاکی شده است.

در اروپا

در حدود سال ۱۳۰۰ میلادی و پس از ترجمهٔ آثاری چون شمس المعارف، کتاب‌های زیادی دربارهٔ مربع‌های جادویی در اروپا نوشته شد. مانوئل موخوپولوس، دانشور یونانی، از نخستین کسانی است که بر ترجمهٔ اثر بونی کار کرده است. در متون اسپانیایی از حدود ۱۲۸۰ میلادی مسائل مرتبط با مربع‌های جادویی دیده می‌شود. این مربع‌ها در ایتالیای قرون وسطی نیز رایج بودند و لوکا پاچیولی روی مربع‌های ابعاد ۳ تا ۹ کار کرد.

آلبرشت دورر

مربع جادویی آلبرشت

مربع جادویی حکاکی‌شده در اثر Melencolia I آلبرشت دورر از نمونه‌های مشهور اروپایی است و به مربع جادویی منسوب به Yang Hui در چین شباهت دارد. عدد جادویی آن ۳۴ است؛ افزون بر سطرها، ستون‌ها و قطرها، مربع چهارتایی میانی و چهار مربع گوشه‌ای نیز مجموع ۳۴ دارند و دو عدد میانی سطر آخر، سال ساخت اثر یعنی ۱۵۱۴ را نشان می‌دهند.

۱۶	۳	۲	۱۳
۵	۱۰	۱۱	۸
۹	۶	۷	۱۲
۴	۱۵	۱۴	۱

ساگرادا فامیلیا

ژوزپ ماریا سوبیراکس مربعی از درجهٔ ۴ در کلیسای ساگرادا فامیلیا حکاکی کرده که عدد آن ۳۳ است. این مربع به مربع دورر شباهت دارد اما مقدار چهار خانه یک واحد کاهش یافته است.

۱	۱۴	۱۴	۴
۱۱	۷	۶	۹
۸	۱۰	۱۰	۵
۱۳	۲	۳	۱۵

این مربع با مربع جادویی معمول تفاوت دارد، زیرا اعداد ۱۰ و ۱۴ دو بار تکرار شده و ۱۲ و ۱۶ در آن نیامده‌اند؛ بنابراین به معنای دقیق ریاضی، مربع جادویی کامل نیست.

در علوم خفیه

سیگیل‌ها و رابطهٔ آن‌ها با مربع جادویی

در بسیاری از فرهنگ‌ها مربع‌های جادویی با سحر و علوم خفیه پیوند داده می‌شده‌اند. بنا بر این سنت، یک روش رایج ساخت سیگیل و طلسم، رسم خط میان اعداد یا حروف روی مربع جادویی بوده است. در این سنت، مربع‌های جادویی ابعاد ۳ تا ۹ را با هفت «سیارهٔ» نجوم کهن مرتبط می‌دانستند. در سال ۱۵۱۰ میلادی هاینریش کورنلیوس آگریپا در کتاب فلسفهٔ علوم خفیه با تکیه بر متون هرمسی، مربع‌های جادویی هفت سیاره را ترسیم کرد؛ این کتاب در اروپا پرآوازه بود. تأکید می‌شود که خواص فراطبیعی نسبت‌داده‌شده به این مربع‌ها اعتقادی است و پشتوانهٔ علمی ندارد.

زحل=۱۵ ۴ ۹ ۲ ۳ ۵ ۷ ۸ ۱ ۶

مشتری=۳۴ ۴ ۱۴ ۱۵ ۱ ۹ ۷ ۶ ۱۲ ۵ ۱۱ ۱۰ ۸ ۱۶ ۲ ۳ ۱۳

مریخ=۶۵ ۱۱ ۲۴ ۷ ۲۰ ۳ ۴ ۱۲ ۲۵ ۸ ۱۶ ۱۷ ۵ ۱۳ ۲۱ ۹ ۱۰ ۱۸ ۱ ۱۴ ۲۲ ۲۳ ۶ ۱۹ ۲ ۱۵

خورشید=۱۱۱ ۶ ۳۲ ۳ ۳۴ ۳۵ ۱ ۷ ۱۱ ۲۷ ۲۸ ۸ ۳۰ ۱۹ ۱۴ ۱۶ ۱۵ ۲۳ ۲۴ ۱۸ ۲۰ ۲۲ ۲۱ ۱۷ ۱۳ ۲۵ ۲۹ ۱۰ ۹ ۲۶ ۱۲ ۳۶ ۵ ۳۳ ۴ ۲ ۳۱

ناهید=۱۷۵ ۲۲ ۴۷ ۱۶ ۴۱ ۱۰ ۳۵ ۴ ۵ ۲۳ ۴۸ ۱۷ ۴۲ ۱۱ ۲۹ ۳۰ ۶ ۲۴ ۴۹ ۱۸ ۳۶ ۱۲ ۱۳ ۳۱ ۷ ۲۵ ۴۳ ۱۹ ۳۷ ۳۸ ۱۴ ۳۲ ۱ ۲۶ ۴۴ ۲۰ ۲۱ ۳۹ ۸ ۳۳ ۲ ۲۷ ۴۵ ۴۶ ۱۵ ۴۰ ۹ ۳۴ ۳ ۲۸

عطارد=۲۶۰ ۸ ۵۸ ۵۹ ۵ ۴ ۶۲ ۶۳ ۱ ۴۹ ۱۵ ۱۴ ۵۲ ۵۳ ۱۱ ۱۰ ۵۶ ۴۱ ۲۳ ۲۲ ۴۴ ۴۵ ۱۹ ۱۸ ۴۸ ۳۲ ۳۴ ۳۵ ۲۹ ۲۸ ۳۸ ۳۹ ۲۵ ۴۰ ۲۶ ۲۷ ۳۷ ۳۶ ۳۰ ۳۱ ۳۳ ۱۷ ۴۷ ۴۶ ۲۰ ۲۱ ۴۳ ۴۲ ۲۴ ۹ ۵۵ ۵۴ ۱۲ ۱۳ ۵۱ ۵۰ ۱۶ ۶۴ ۲ ۳ ۶۱ ۶۰ ۶ ۷ ۵۷

ماه=۳۶۹ ۳۷ ۷۸ ۲۹ ۷۰ ۲۱ ۶۲ ۱۳ ۵۴ ۵ ۶ ۳۸ ۷۹ ۳۰ ۷۱ ۲۲ ۶۳ ۱۴ ۴۶ ۴۷ ۷ ۳۹ ۸۰ ۳۱ ۷۲ ۲۳ ۵۵ ۱۵ ۱۶ ۴۸ ۸ ۴۰ ۸۱ ۳۲ ۶۴ ۲۴ ۵۶ ۵۷ ۱۷ ۴۹ ۹ ۴۱ ۷۳ ۳۳ ۶۵ ۲۵ ۲۶ ۵۸ ۱۸ ۵۰ ۱ ۴۲ ۷۴ ۳۴ ۶۶ ۶۷ ۲۷ ۵۹ ۱۰ ۵۱ ۲ ۴۳ ۷۵ ۳۵ ۳۶ ۶۸ ۱۹ ۶۰ ۱۱ ۵۲ ۳ ۴۴ ۷۶ ۷۷ ۲۸ ۶۹ ۲۰ ۶۱ ۱۲ ۵۳ ۴ ۴۵

در سنت خفیه ادعا شده است که ساخت مربع‌های جادویی به این شیوه راهی برای «ارتباط با ارواح، اجنه و شیاطین» فراهم می‌کند؛ چنین ادعایی مبنای واقعی ندارد. در بسیاری از جادونامه‌ها به‌جای عدد از حرف استفاده می‌شد. برای نمونه، مربع ساتور که در جادونامه‌هایی چون کلید کوچک‌تر سلیمان آمده و در سنت عامیانه به آن خاصیتی برای دفع «چشم‌زخم» نسبت داده شده است:

S A T O R A R E P O T E N E T O P E R A R O T A S

شعر

اشعاری در بیان رموز این سنت سروده شده که نمونهٔ زیر یکی از آن‌هاست:

حکمای زمانه ماضی		که همه اهل دانشند و هنر
وضع در هندسه نهادستند		که بود بیت خانه نه پیکر
وضع نامش بود سه اندر سه		بنگارم کنون به نقش صور
عدد نقش خانه دور ببین		هست از اعداد نام هفت اختر
شش جهاتست خانه ششمین		خانه چهار نیست نه بشمر
خانه پنجمین که میزانست		شکل پنجست ای فرشته سیر
ششمین خانه یک عدد دارد		هفتمین خانه چار طبع مگر

انواع وفق‌ها در سنت اوفاق

بر پایهٔ منابع اوفاق، وفق‌ها بر دو گونه دسته‌بندی شده‌اند:

الف) تقسیمات شکلی، شامل مربع، مثلث و دایره.

ب) تقسیمات عددی: زوج‌الزوج، زوج‌الفرد و فردالفرد.

مربع‌ها به ثوانی، ثلاثی، رباعی و خماسی و نیز به عددی و ذوالکتابه تقسیم شده‌اند؛ در دستهٔ مثلث نیز اشکالی چون مثلث کامل، مثلث هندی و خاتم سلیمانی نام برده شده است. این تقسیم‌بندی‌ها به سنت خفیه مربوط‌اند و بار ریاضی ندارند.

لوح صد اندر صد

در برخی منابع اسلامی آمده است که نخستین کسی که «لوح صد اندر صد» را تدوین کرد علی بن ابی‌طالب بوده است. بنا بر همین منابع، گفته می‌شود این لوح دربردارندهٔ آیات و کلمات کتب آسمانی و «اسم اعظم» است؛ این انتساب جنبهٔ روایی و اعتقادی دارد.

روش ساخت مربع‌های جادویی

برای ساخت مربع‌های جادویی روش‌های گوناگونی وجود دارد. برای هر n بزرگ‌تر از ۲ مربع جادویی موجود است و تنها برای n=۲ جوابی نداریم. مربع‌های جادویی را بر پایهٔ n به سه دسته تقسیم می‌کنند: n فرد، n=۴k و n=۴k+۲. تعیین شمار مربع‌های جادویی درجهٔ n برای n>۵ از مسائل حل‌نشدهٔ ریاضی است؛ برای نمونه شمار مربع‌های جادویی n×n برای n=۱، ۲، ۳، ۴ و ۵ به‌ترتیب برابر است با:

۱، ۰، ۱، ۸۸۰، ۲۷۵٬۳۰۵٬۲۲۴

روش نخست برای مربع‌های درجه فرد

خانهٔ وسط را مشخص کرده و یک خانه زیر آن را با ۱ پر می‌کنیم، سپس در راستای قطر پایین-راست پیش می‌رویم. هرگاه به خانه‌ای بیرون از مربع رسیدیم، به بالاترین خانهٔ خالی همان سطر یا ستون بازمی‌گردیم. اگر به خانه‌ای پُر رسیدیم، جهت را به سمت پایین-چپ تغییر می‌دهیم و ادامه می‌دهیم تا همهٔ خانه‌ها پر شوند.

روش دیگر برای مربع‌های درجه فرد

اگر n فرد باشد، به هر ضلع مربع از هر سو یک ضلع دیگر به اندازهٔ n−۲ خانه (از وسط) می‌افزاییم و این کار را تا رسیدن به ضلع یک‌خانه‌ای ادامه می‌دهیم. سپس خانه‌ها را به شیوهٔ استاندارد پر کرده و اعدادِ بیرون از مربع n×n را روی همان سطر یا ستون، به تعداد خانه‌ای برابر با درجهٔ مربع، به درون منتقل می‌کنیم تا مربع جادویی ساخته شود.

روش مربع‌های درجهٔ مضرب ۴

اقطار مربع را در بلوک‌های ۴×۴ در نظر می‌گیریم. نخست اعداد ۱ تا n² را به‌ترتیب در سطرها می‌نویسیم اما تنها خانه‌های روی قطرها را پر می‌کنیم و بقیه را خالی می‌گذاریم. سپس از انتها، اعداد را دوباره شمرده و این بار در خانه‌های خالی می‌نویسیم.

جستارهای وابسته

• مربع لوشو
• سودوکو

منابع

• Eric W. Weisstein, Magic Square at MathWorld.
• Magic Squares at Convergence
• W. S. Andrews, Magic Squares and Cubes (New York: Dover, 1960), originally printed in 1917.
• John Lee Fults, Magic Squares (La Salle, Illinois: Open Court, 1974).

پیوند به بیرون

• Manuel Moschopoulos — Mathematics and the Liberal Arts