گراف جانسون

Johnson graph
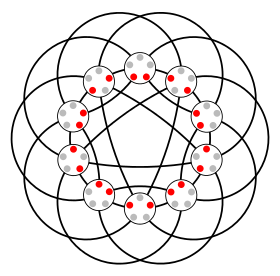The Johnson graph J(5,2)
Named after	Selmer M. Johnson
راس	${\binom {n}{k}}$
ضلع	${\frac {k(n-k)}{2}}{\binom {n}{k}}$
فاصله در گراف	$\min(k,n-k)$
ویژگی‌های	$(k(n-k))$-regular Vertex-transitive Distance-transitive Hamilton-connected
قراردادهای نوشتاری	$J(n,k)$

گراف جانسون یک نوع خاص از گراف بدون جهت تعریف شده از نظام مجموعه ها است. رئوس گراف جانسون ${\displaystyle }$ هستند؛ ${\displaystyle }$زیرمجموعه از یک مجموعه با ${\displaystyle }$; دو راسی مجاور هستند که تقاطع دو راس (زیر مجموعه) شامل ${\displaystyle }$. هر دوی گراف جانسون  و جانسون طرح به نام سلمر مارتین جانسون نام گذاری شده است.

موارد خاص

• ${\displaystyle }$ گراف کامل K_n است.
• ${\displaystyle }$  گراف هشت وجهی است.
• ${\displaystyle }$ گراف مکمل برای گراف پترسن است، بنابراین گراف خط   K₅ است. به طور کلی، به ازای هر n، گراف جانسون ${\displaystyle }$ مکمل گراف نسر ${\displaystyle }$

ویژگی های نظ

• $J(n,k)$ گراف هم ریخت گراف $J(n,n-k)$.
• $0\leq j\leq \mathrm {diam} (J(n,k))$ هر جفت از رئوس که در فاصله $j$ $k-j$. مسیر همیلتونی
• $J(n,k)$ مسیر همیلتونی است، به این معنی که هر جفت از رئوس، مقصد مسیر همیلتونی را در گراف شکل می دهند .
• $J(n,k)~$ $~k(n-k)$.
• $J(n,k)$ گرافی با رئوس و یال ها از چندبری با ابعاد ( n - 1 ) می سازد که hypersimplex نام دارد.
• $\omega \left(J(n,k)\right)=1-{\frac {\lambda _{\mathrm {max} }}{\lambda _{\mathrm {min} }}}$گروهک$J(n,k)$ با کمترین و بیشترین مقدار آن یعنی $\lambda _{\mathrm {min} }$$\lambda _{\mathrm {max} }$.
• $\chi (J(n,k))\leq n$ $J(n,k)$ حداکثر به $n$.

گروه خودسازی

یک زیر گروه فاصله-متعدی از هم ریخت ${\displaystyle }$ به ${\displaystyle }$. در واقع ${\displaystyle }$ ≅ ${\displaystyle }$مگر اینکه ${\displaystyle }$; در غیر این صورت ${\displaystyle }$ ≅ ${\displaystyle }$.

آرایه تقاطع

به عنوان یک نتیجه از در فاصله-متعدی بودن، همچنین با فاصله منظم بودن ${\displaystyle }$. ${\displaystyle }$ ${\displaystyle }$ به صورت ${\displaystyle }$ نمایش داده می شود که در آن:

• ${\displaystyle }$ برای همه ${\displaystyle }$.
• ${\displaystyle }$ برای همه ${\displaystyle }$.

مگر آنکه ${\displaystyle }$ ${\displaystyle }$; آرایه تقاطع ${\displaystyle }$ با سه گراف دیگر با فاصله منظمی که گراف جانسون نباشند به اشتراک گذاشته می شود.

مقادیر ویژه و بردارهای ويژه

• مشخصه چند جمله ای ${\displaystyle }$ به روش زیر به دست می آید: ${\displaystyle }$.
• این بردارهای ويژه از ${\displaystyle }$ توصیف صریحی دارند.

رابطه با طرح جانسون

گراف جانسون ${\displaystyle }$ رابطه نزدیکی با  طرح جانسون دارد، یک طرح انجمنی که در آن هر جفت از k عضو مجموعه در ارتباط با عددی است که نصف اندازه تفاضل متقارن این دو مجموعه است. گراف جانسون برای هر جفت از مجموعه ها که فاصله آن ها در طرح انجمنی یکی است، یک یال دارد، و فواصل در طرح انجمنی دقیقا کوتاهترین مسیر در گراف جانسون است.

طرح جانسون همچنین با دیگر خانواده ها از مسیر-متعدی،  گراف های فرد که رئوس آن ها دارای زیر مجموعه هایی با ${\displaystyle }$ از مجموعه ای شامل ${\displaystyle }$.

مشکلات حل نشده

ویژگی های گسترش راس از گراف جانسون به خوبی ساختار متناظر مجموعه های رئوس از اندازه داده شده، به طور کامل قابل فهم نیست. اگرچه، به طور متناوب محدوده کوچک تر در گسترش مجموعه های بزرگ از رئوس، به تازگی به دست آمده است.

به طور کلی، در تعیین تعداد رنگ ها برای گراف جانسون یک مشکل حل نشده است.