گراف فاکتور بحرانی
در نظریه گرافها، یک مبحث ریاضی، گراف فاکتور بحرانی یا گراف هایپومچبل (به انگلیسی: Factor-critical graph) یک گراف با n راس میباشد به طوری که هر زیر گراف n-1 عضوی دارای خاصیت تطابق کامل میباشد.(تطابق کامل در یک گراف به این معنی است که یک زیر مجموعه از یالهای این گراف هستند که در این زیر مجموعه هر یک از راسها دقیقاً نقطه پایانی یکی از یالها هستند.
نوع دیگری از اتصال که در آن تمامی راسها به جز یکی از آنها پوشش داده میشوند تطابق کامل نزدیک(near-perfect matching) نامیده میشود. پس بهطور مشابه یک گراف فاکتور_بحرانی گرافی است که در آن تطابقهای کامل نزدیک وجود داشته باشد طوری که در هر کدام از یکی از راسها صرف نظر شده باشد.
نمونهها[ویرایش]

هر دور به طول فرد یک گراف فاکتور_بحرانی میباشد، همانطور که هر گراف کامل با تعداد فرد راس یک گراف فاکتور_بحرانی میباشد. بهطور عمومی هر گراف همیلتونی با تعداد فرد راس یک گراف فاکتور_بحرانی میباشد. گرافهای دوستی یا friendship graphs (گرافهایی که از اتصال مجموعهای از مثلثها به وجود آمده و در یک راس مشترک هستند) مثال دیگری از گراف فاکتور_بحرانیها هستند با این تفاوت که این گرافها غیر همیلتونی هستند. هر گراف همبند پنجه آزاد(claw-free) با تعداد فرد راس، یک گراف فاکتور_بحرانی میباشد. برای مثال گراف ۱۱ راسی که از حذف یک راس از بیست وجهی منتظم به وجود میآید و همبند نیز میباشد، یک گراف فاکتور_بحرانی میباشد. این نتیجه بهطور مستقیم از یک قضیه بنیادی تر با این مضمون که هر گراف پنجه آزادِ همبند که دارای تعدادی زوج راس باشد حتماً دارای یک تطابق کامل میباشد، حاصل میشود.
تعاریف و توصیفات[ویرایش]

گرافهای فاکتور- بحرانی را میتوان با چندین راه مختلف توصیف و تشریح کرد، جدا از تعریف آنها به عنوان گرافهایی که در آنها با حذف یک راس میتوان یک تطابق کامل ایجاد کرد، تعاریف و ویژگیهای دیگری نیز دارند به این صورت که:
Tibor Gallai ثابت کرد که گرافی میتواند فاکتور-بحرانی باشد اگر و تنها اگر همبند باشد و به ازای هر راس v از گراف، یک تطابق حداکثری وجود داشته باشد طوری که شامل راس v نشود. این نتیجه از این ویژگی که گراف باید دارای تعدادی فرد راس بوده طوری که هر تطابق حداکثر باید همه راسها به جز یکی را به هم مرتبط کند، استنتاج میشود.
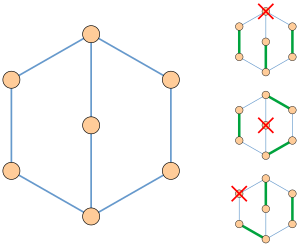
لاسلو لوواس نیز ثابت کرد که گرافی فاکتور بحرانی میباشد اگر و تنها اگر تعدادی فرد تجزیه گوشی داشته باشد (یک دستهبندی از یالهای گراف به دنبالهای از زیرگرافها گفته میشود به طوری که هر یک از این زیرگرافهای دارای دور یا مسیری به طول فرد باشند، به این ترتیب که اولین زیرگراف یک دور باشد و بعد از آن زیرگرافها هرکدام مسیری باشند که دارای نقطههای پایانی هستند و هر راس داخلی نباید در زیرگراف قبلی وجود داشته باشد، همچنین هر دور به غیر از دور اول در دنباله دقیقاً یک راس در زیرگرافهای قبلی داشته باشد. برای مثال گراف نمایش داده شده در شکل ممکن است با این روش به یک دور با ۵ یال و یک مسیر با ۳ یال تقسیمبندی شود. در مواردی که تطابق کامل نزدیک برای گراف فاکتور بحرانی داده شود، دستههای جدا شدنی میتوانند به نحوی انتخاب شوند که دستههای جدا شدنی بین یالهای تطبیق یافته و تطبیق نیافته متبادل شوند.
یک گراف همچنین فاکتور بحرانی است اگر و تنها اگر بتوان این گراف را به وسیله دنبالهای از ادغامهای دورهای به طول فرد به یک گراف ساده تبدیل کرد. علاوه بر این، در این توصیف این امکان وجود دارد تا هر دور در این دنباله را طوری انتخاب کرد که شامل یک راس که از ادغام دور قبلی که به وجود آمده است، باشد. برای مثال اگر یکی, دستههای یک تجزیه گوشی را قطع کند، به ترتیبی که دستهها تجزیه شدهاند، سپس در هر زمان که یکی از دستهها قطع میشود، یک دور فرد به وجود میآید، به همین منظور این ویژگی دستههای جدا شدنی میتواند برای یافتن دنبالهای از دورهای فرد برای ادغام استفاده شود. بهطور عکس از دنبالهای از ادغام دورهای فرد که هر کدام شامل یک راس که از ادغام قبلی میباشد، میتوان یک دسته تجزیه پذیر به وجود آورد به طوری که دستهها مجموعهای از یالهای ادغام شده در هر مرحله باشند.
فرض کنید که گراف G به همراه یک راس منتخب و برگزیده به نام V و یک تطابق به نام M که همه راسها به غیر از V را پوشش میدهد داده شدهاست. پس G زمانی فاکتور بحرانی است اگر و تنها اگر مجموعهای از مسیرها در G وجود داشته باشد طوری که یک در میان از بین یالهای انطباق یافته و انطباق نیافته، راس V را به سایر راسها در G وصل کنند. بر اساس این ویژگی ما میتوانیم در زمان خطی تشخیص بدهیم که آیا گراف G با تطابق کامل نزدیک داده شده فاکتور بحرانی هست یا نه.
خواص و ویژگی ها[ویرایش]
گرافهای فاکتور_بحرانی همیشه تعداد فرد راس دارند و نیز باید همبندی دو یالی داشته باشند (به این معنی که نباید هیچ پلی داشته باشند). با این وجود ضرورتی ندارد که هر دو راس در این گرافها همبند باشند، گرافهای دوستی (friendship) میتوانند یک نوع مثال نقض در این رابطه باشند. دو بخشی بودن گراف فاکتور_بحرانیها امری غیرممکن است، زیرا در گراف دوبخشی با یک تطابق کامل، تنها راسهایی که در قسمت بزرگتر گراف دوقسمتی هستند میتوانند با حذف خود یک گراف دارای تطابق کامل تولید کنند.
هر گراف فاکتور_بحرانی با m یال که دو راس-همبند میباشد، حداقل دارای m عدد تطابق کامل مختلف میباشد، بهطور کلی هر گراف فاکتور_بحرانی با m یال و c بلوک (اجزای دو راس همبند) حداقل عدد تطابق نزدیک مختلف دارد. گرافهایی که این محدودیتها و ویژگیها را شامل میشوند، به گرافهایی با تعداد فرد دسته تجزیه پذیر به یک شکل خاص توصیف میشوند.
هر گراف همبند میتواند با قطع کردن تعداد کافی از یالهایش به یک گراف فاکتور_بحرانی تبدیل شود. حداقل مجموعهای از یالها را که برای تبدیل گراف G به یک گراف فاکتور_بحرانی لازم است قطع کنیم اساس matroid را تشکیل میدهد. Matroid قضیهای است که به یک الگوریتم حریصانه برای یافتن کمترین وزن مجموعهای از یالها که باید قطع شوند تا در زمان چند جملهای یک گراف فاکتور_بحرانی را بسازند، اشاره میکند.
برنامهها[ویرایش]
یک بلاسوم(blossom) یک زیردرخت فاکتور-بحرانی از یک گراف بزرگ است. Blossom یک نقش کلیدی در الگوریتم Jack Edmodns برای تطابق حداکثر و تطابق در وزن حداقل در گرافهای غیر دو بخشی ایفا میکند.
در ترکیبهای چند ضلعی، گرافهای فاکتور-بحرانی یک نقش کلیدی در توضیح شکلهای تطابق یا تطابق جنگلهای چندگانهٔ از یک گراف داده شده ایفا میکند.
کلیات و مفاهیم مرتبط[ویرایش]
گرافی k-factor-critical است اگر هر زیرگراف n-k راسی دارای یک تطابق کامل باشد. بر طبق این تعریف گراف hypomatchable یک 1-factor-critical بهشمار میآید. علاوه بر این بهطور کلی تر یک گراف (a,b)-factor-critical است اگر هر زیر گراف n-k رأسی r عامل مشترک داشته باشد به این صورت که این r عامل مجموعهٔ رأسهای یک زیر گراف r-منظم از گراف داده شده باشند.
یک گراف critical (بدون قید و شرط) معمولاً این گونه تفسیر میشود که حذف هر یک از رأسها تعداد رنگهای لازم برای رنگ آمیزی این گراف را کاهش میدهد. مفهوم critical بودن بهطور عمومی در نظریه گرافها اشاره بر این دارد که حذف هر رأسِ ممکن بعضی از ویژگیهای وابسته به گراف را تغییر میدهد و بعضی را تغییر نمیدهد. یک matching-critical graph گرافی است که حذف هر رأس اندازه بیشترین تطابق را تغییر نمیدهد و طبق تعریف Gallai , گرافهای matching-critical گرافهایی هستند که هر جزء همبند یک factor-critical میباشد. گراف مکمل یک گراف critical لزوماً matching-critical میباشد، این در واقع اصلی بود که Gallai از آن برای اثبات کران پایین تعداد رأسهای یک critical graph استفاده کرد. در نظریه گراف پیشرفته، مفهوم factor-criticality با تعریف نوعی از دستههای جداشدنی روی matroid و توصیف matroid به عنوان یک factor-critical با این شرط که matroid دستهای جداشدنی داشته باشد که تمام دستهها فرد باشند، به قضیه matroid بسط داده شدهاست.

