مسئله تاریخ تولد

در تئوری احتمالات، مسئله تاریخ تولد یا پارادوکس تاریخ تولد به یافتن احتمال حضور بیش از دو نفر در مجموعهٔ تصادفی n نفره که تاریخ تولد یکسانی داشته باشند، مربوط است. طبق اصل لانه کبوتری این احتمال وقتی که تعداد افراد حاضر برابر با ۳۶۶ (با فرض این که سال ۳۶۵ روز است، بدون در نظر سال کبیسه) شود، مساوی ۱۰۰٪ می‌شود. اگرچه احتمال ۹۹٪ وقتی که تعداد افراد تنها برابر ۵۷ نفر است حاصل می‌شود. همچنین با احتمال ۵۰٪ حداقل دو نفر تولد یکسانی بین ۲۳ نفر دارند. این نتایج با این فرض به دست می‌آید که سال دارای ۳۶۵ روز (بجز ۳۰ اسفند) و احتمال تولد افراد در آن‌ها برابر هم باشد.

محاسبات ریاضی پشت این مسئله باعث ایجاد یک حمله رمزنگاری معروف به اسم حمله روز تولد شده‌است. این حمله بر اساس مدل احتمالی مسئله تاریخ تولد، پیچیدگی توابع درهم‌سازی را کاهش می‌دهد و باعث ساده شدن شکستن آن می‌شود.

نموداری که به طور تقریبی احتمال حضور حداقل ۲ نفر را بین مجموعه تصادفی از افراد نشان می‌دهد.

فهم مسئله

مسئله روز تولد این سوال را مطرح می کند که آیا درون یک گروه معین هیچ فردی وجود دارد که با یکی دیگر از افراد گروه تاریخ تولد مشابهی داشته باشد - نه شخص خاصی به طور مشخص. (به قسمت "#هم تاریخ تولد با شما" در زیر نگاه کنید برای تحلیل این مسئله جایگزینی که کمتر جالب به نظر می رسد.) در مثالی که پیش از این مطرح شد، در لیستی شامل 23 نفر، در مقایسه شانس اینکه تاریخ تولد نفر اول لیست با دیگران یکسان باشد 22 است، برای نفر دوم لیست برابر با 21، برای نفر سوم لیست برابر با 20 و همین طور تا آخر. از این رو مجموع شانس ها برابر است با : 22+21+21+...+1 = 253، بنابراین مقایسه هر فرد با تمام افراد دیگر 253 شانس مجزا را به وجود می آورد (ترکیب): در یک گروه 23 نفری (23¦2)= 23.22/2=253جفت وجود دارد. با فرض اینکه احتمال تمام روزهای تولد یکسان باشد، احتمال یک تاریخ تولد داده شده برای فردی که به طور تصادفی از بین جمع انتخاب شده 1/365 (با نادیده گرفتن روز کبیسه، 30 اسفند) است.اگرچه زوج هایی که در یک گروه 23 نفری هستند از لحاظ آماری با 253 زوجی که به طور مستقل انتخاب شده‌اند هم ارز نیستند، اگر یک گروه بر حسب تعداد زوج های آن سنجیده شود، پارادوکس تولد نسبت به زمانی که بر حسب افراد سنجیده شود، کم تر تعجب برانگیز خواهد بود.

محاسبه احتمالات

مسئله مورد نظر، محاسبه احتمال تقریبی حضور حداقل دو نفر در اتاقی با حضور n نفر، با تاریخ تولد یکسان است. برای سادگی، تفاوت ها در توزیع، مانند سال کبیسه، دوقلوها، تغییرات روزهای هفته و تغییرات فصلی را نادیده بگیرید و فرض کنید 365 تاریخ تولدی که امکان پزیرند، احتمال برابری داشته باشند. توزیع تاریخ تولدها در واقعیت یکنواخت نیست، زیرا تمام تاریخ ها احتمال برابری ندارند. اگر P(A) احتمال حضور حداقل 2 نفر در یک اتاق با تاریخ تولدهای یکسان باشد، محاسبه P(A’)، یعنی احتمال نبود هیچ دو نفری که تولد یکسان داشته باشند می تواند آسان تر باشد. بنابراین، به این دلیل که P(A) و P(A') تنها احتمالات ممکن و دو به دو ناسازگار هستند، P(A') = 1 − P(A)). برای احترام به راه حل های منتشر شده ی زیادی که نتیجه گرفته‌اند برای داشتن P(A) بیش تر از 50% حضور 23 نفر ضروری است، در زیر، برای محاسبه P(A)، 23 نفر به عنوان مثال در نظر گرفته می شود. وقتی رویدادها مستقل از یکدیگر باشند، احتمال کل رویدادهایی که اتفاق می افتند برابر است با ضرب احتمالات هر کدام از رویدادها. بنابراین اگر P(A') به عنوان 23 رویداد مستقل تعریف شود، می توان به این صورت آن را محاسبه کرد:

P(1) × P(2) × P(3) × ... × P(23)

این 23 رویداد مستقل، متناظر با این 23 نفر هستند و می توانند به ترتیب تعریف شوند. هر رویداد می تواند با فرد متناظر با آن که با هیچ یک از افراد تحلیل شده قبلی، تاریخ تولد یکسانی ندارد مشخص شود. برای رویداد 1، هیچ فرد تحلیل شده ی قبلی وجود ندارد. بنابراین احتمال P(1) یعنی اینکه تاریخ تولد فرد شماره 1 با هیچ یک از افراد تحلیل شده ی قبلی یکسان نباشد، 1 یا 100% است. بدون در نظر گرفتن سال های کبیسه برای این تحلیل، به دلایلی که در زیر به روشنی خواهد آمد، احتمال برابر با یک می تواند به صورت 365/365 نوشته شود. برای رویداد 2، تنها فرد تحلیل شده ی قبلی نفر 1 است. با فرض اینکه تاریخ تولدها احتمال برابری برای اتفاق افتادن در هریک از 365 روز سال را داشته باشند، احتمال P(2)، اینکه فرد شماره 2 تاریخ تولد متفاوتی با فرد شماره 1 داشته باشد، 364/365 است. این به این دلیل است که اگر فرد شماره 2 در هر کدام از 364 روز دیگر سال متولد شده باشد، فرد شماره 1 و 2 تاریخ تولد یکسانی نخواهند داشت. به طور مشابه اگر فرد شماره 3 در هریک از 363 روز دیگر سال غیر از تاریخ تولد فرد شماره 1 و 2 متولد شده باشد، فرد شماره 3 تاریخ تولد یکسانی با آن ها نخواهد داشت. در نتیجه P(3)=363/365. این تحلیل تا رسیدن به فرد شماره 23 ادامه پیدا می کند، فردی که احتمال آنکه تاریخ تولد یکسانی با افراد تحلیل شده ی قبلی نداشته باشد، یعنی P(23)، 343/365 است. P(A’) برابر با ضرب این احتمالات مجزاست:

(1) P(A') = 365/365 × 364/365 × 363/365 × 362/365 × ... × 343/365

می توان عبارات معادله 1 را اینگونه جمع بندی کرد:

(2) P(A') = (1/365)²³ × (365 × 364 × 363 × ... × 343)

با محاسبه معادله 2 مقدار P(A’)=0.492703 بدست می آید. بنابراین P(A) = 1 − 0.492703 = 0.507297 (50.7297%) این روند می تواند برای یک گروه n نفره تعمیم داده شود، به طوریکه p(n) احتمال وجود حداقل دو نفر از این n نفر است که تاریخ تولد یکسانی دارند. ساده تر این است که ابتدا احتمال pˉ(n)، یعنی اینکه تمام n تاریخ تولدها متفاوت باشند محاسبه شود. با توجه به اصل لانه کبوتری اگر n˃365 باشد، pˉ(n) صفر است. اگر n≤365 باشد آنگاه:

$\begin{align} \bar p(n) &= 1 \times \left(1-\frac{1}{365}\right) \times \left(1-\frac{2}{365}\right) \times \cdots \times \left(1-\frac{n-1}{365}\right) \\ &= { 365 \times 364 \times \cdots \times (365-n+1) \over 365^n } \\ &= { 365! \over 365^n (365-n)!} = \frac{n!\cdot{365 \choose n}}{365^n}\end{align}$

که در اینجا ‘!’ عمل فاکتوریل و factorial operator and ${365 \choose n}$ ضریب دو جمله ای را نشان می دهد. این معادله این حقیقت را تشریح می کند که در نبود افرادی که تاریخ تولد یکسان داشته باشند، یک نفر دوم نمی‌تواند تاریخ تولد مشابهی با نفر اول داشته باشد (364/365)، سومی نمی‌تواند تاریخ تولد یکسانی با دو تای اول داشته باشد (363/365)، و در کل nامین تاریخ تولد نمی‌تواند با n-1 تاریخ تولد قبلی یکسان باشد. این رویداد که حداقل دو نفر از n نفر تاریخ تولد یکسان داشته باشند، متمم این است که کل n تاریخ تولدها متفاوت باشند. بنابراین احتمال آن، یعنی p(n) برابر است با:

$p(n) = 1 - \bar p(n). \,$

احتمال تقریبی این که هیچ دو نفری در یک گروه n نفری تاریخ تولد یکسان نداشته باشند. توجه کنید که مقیاس عمودی لگاریتمی است (به ازای هر واحد کم شونده 1020 مرتبه احتمال، کم ترمی شود).

این احتمال برای n=23 از ½ بیش تر است (با مقداری در حدود 50.7%). جدول زیر این احتمال را برای برخی مقادیر دیگر n نشان می دهد (این جدول همانطور که در بالا شرح داده شد، از وجود سالهای کبیسه چشم پوشی می کند):

n	p(n)
10	11.7%
20	41.1%
23	50.7%
30	70.6%
50	97.0%
57	99.0%
100	99.99997%
200	99.9999999999999999999999999998%
300	(100 − (6×10−80))%
350	(100 − (3×10−129))%
365	(100 − (1.45×10−155))%
366	100%

تقریت ها

نمودار نمایش صحت تقریب $1-e^{-n^2/(2 \times 365)}$

بسط سری تیلور برای تابع نمایی به صورت زیر است:(ثابت e تقریباً برابر است با 2.718281828):

$e^x = 1 + x + \frac{x^2}{2!}+\cdots$

که اولین نوع تقریب برای ex در x«1 را به دست می دهد:

$e^x \approx 1 + x.\$

برای به کار بردن این تقریب در اولین عبارت به دست آمده برای p(n)، $x = -i / 365\$ قرار دهید.آنگاه $e^{-i/365} \approx 1 - i/365 \$ سپس برای هر عبارت در فرمول p(n) $1 - i/365 \approx e^{-i/365} \$.

برای i=1، $1 - 1/365 \approx e^{-1/365} \$

اولین عبارتی که برایp(n) بدست آمد، می تواند به صورت زیر تخمین زده شود:

$\begin{align} \bar p(n) & \approx 1 \times e^{-1/365} \times e^{-2/365} \cdots e^{-(n-1)/365} \\ & = 1 \times e^{-(1+2+ \cdots +(n-1))/365} \\ & = e^{-(n(n-1)/2) / 365}. \end{align}$

در نتیجه:

$p(n) = 1-\bar p(n) \approx 1 - e^{- n(n-1)/(2 \times 365)}.$

یک تقریب غیر دقیق تر که معادل این عبارت است به صورت زیر است:

$p(n)\approx 1-e^{- n^2/(2 \times 365)},\,$

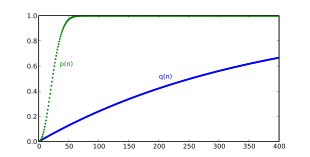
که همانگونه که نمودار نشان می دهد، تقریباً صحیح است. درک این مطلب ساده است که یک روش مشابه برای هر تعداد از "نفرات" و "روزها" می تواند به کار رود. اگر به جای 365 روز، n روز را در نظر بگیریم و m نفر وجود داشته باشند و m«n باشد، آنگاه با استفاده از روش بالا به این نتیجه می رسیم که اگر Pr[(n, m)] احتمال حضور حداقل دو نفر خارج از m نفر که از میان یک مجموعه n روزه تاریخ تولد یکسان دارند باشد، آنگاه: $Pr[(n, m)] \approx 1-e^{-m^2 / 2n}.\$

یک توان ساده

احتمال حضور هر دو نفری که تاریخ تولد یکسان نداشته باشند 364/365 است. در یک اتاق شامل n نفر،C(n, 2)=n(n-1)/2 تعداد زوج از نفرات حضور دارند، یعنی C(n, 2)رویداد. احتمال عدم حضور دو نفر که تاریخ تولد یکسانی داشته باشند، می تواند با این فرض که این رویدادها مستقل اند و بنابراین با ضرب احتمالات آنها در یکدیگر تخمین زده شود. مختصراً 364/365 می تواندC(n, 2) بار در خودش ضرب شود که در این صورت خواهیم داشت:

$\left(\frac{364}{365}\right)^{C(n,2)}.$

و اگر این، احتمال عدم حضور فردی با تولد یکسان باشد، آنگاه احتمال اینکه برخی نفرات تاریخ تولد یکسان داشته باشند به صورت زیر است:

$p(n) \approx 1 - \left(\frac{364}{365}\right)^{C(n,2)}.$

تقریب پوواسون

با استفاده از تقریب پوواسون برای این دوجمله ای داریم:

$\mathrm{Poi}\left(\frac{C(23, 2)}{365}\right) =\mathrm{Poi}\left(\frac{253}{365}\right) \approx \mathrm{Poi}(0.6932)$

$\Pr(X>0)=1-\Pr(X=0)=1-e^{-0.6932}=1-0.499998=0.500002.$

که باز هم این بالای 50% است.

تقریب تعداد افراد

این مسئله نیز می تواند به وسیله فرمول زیر برای تعداد نفراتی که حضورشان برای داشتن حداقل 50% شانس برای تطبیق ضروری است تخمین زده شود:

$n \approx \frac{1}{2} + \sqrt{\frac{1}{4} - 2 \times 365 \times \ln(0.5)} = 22.999943.$

این، نتیجه ای برای این تخمین مناسب است که اگر یک رویداد با احتمال 1 در k، k ln 2 مرتبه تکرار شود، برای حداقل یک بار اتفاق افتادن 50% شانس دارد.

جدول احتمال

مقاله اصلی: ''حمله روز تولد''

length of hex string	#bits	hash space size (2#bits)	Number of hashed elements such that (probability of at least one hash collision) = p
			p = 10−18	p = 10−15	p = 10−12	p = 10−9	p = 10−6	p = 0.1%	p = 1%	p = 25%	p = 50%	p = 75%
8	32	4.3 × 109	2	2	2	2.9	93	2.9 × 103	9.3 × 103	5.0 × 104	7.7 × 104	1.1 × 105
16	64	1.8 × 1019	6.1	1.9 × 102	6.1 × 103	1.9 × 105	6.1 × 106	1.9 × 108	6.1 × 108	3.3 × 109	5.1 × 109	7.2 × 109
32	128	3.4 × 1038	2.6 × 1010	8.2 × 1011	2.6 × 1013	8.2 × 1014	2.6 × 1016	8.3 × 1017	2.6 × 1018	1.4 × 1019	2.2 × 1019	3.1 × 1019
64	256	1.2 × 1077	4.8 × 1029	1.5 × 1031	4.8 × 1032	1.5 × 1034	4.8 × 1035	1.5 × 1037	4.8 × 1037	2.6 × 1038	4.0 × 1038	5.7 × 1038
(96)	(384)	(3.9 × 10115)	8.9 × 1048	2.8 × 1050	8.9 × 1051	2.8 × 1053	8.9 × 1054	2.8 × 1056	8.9 × 1056	4.8 × 1057	7.4 × 1057	1.0 × 1058
128	512	1.3 × 10154	1.6 × 1068	5.2 × 1069	1.6 × 1071	5.2 × 1072	1.6 × 1074	5.2 × 1075	1.6 × 1076	8.8 × 1076	1.4 × 1077	1.9 × 1077

مربع های سفید در این جدول تعداد هش های مورد نیاز برای رسیدن به احتمال رخداد تصادم (ستون) در یک فضای هش داده شده از یک اندازه معین به بیت(ردیف) را نشان می دهد.

(با استفاده از مقایسه تولدها: "اندازه فضای هش" (ردیف ها) "365 روز" خواهند بود. "احتمال تصادم" (ستون ها) 50% خواهند بود و "تعداد نفرات مورد نیاز" 26 نفر خواهد بود (تقاطع ستون ها و ردیف ها). همچنین از این جدول می توان برای تعیین کوچک ترین hash size مورد نیاز استفاده کرد (کران های بالای معین روی hash ها و احتمال خطا)، یا احتمال تصادم (برای تعداد ثابت hash ها و احتمال خطا).

برای مقایسه،

10⁻¹⁵

تا

10⁻¹⁸

سرعت خطای بیت اصلاح نشدنی برای یک دیسک سخت نوعی است. در تئوری، MD5، 128 بیت، باید تا تقریباً 820 میلیارد سند در آن محدوده باقی بماند، حتی اگر این احتمال وجود داشته باشد که تعداد خروجی ها بسیار بیشتر باشد.

منابع

• Coincidences: the truth is out there Experimental test of the Birthday Paradox and other coincidences
• http://www.efgh.com/math/birthday.htm
• http://planetmath.org/encyclopedia/BirthdayProblem.html
• Eric W. Weisstein, Birthday Problem at MathWorld.
• A humorous article explaining the paradox
• SOCR EduMaterials activities birthday experiment
• Understanding the Birthday Problem (Better Explained)