فهرست مرکزهای هندسی

در این مقاله فهرست مرکزوارهای چند شکل گفته شده است. فرض بر این است که تمامی شکل ها همگن اند.

نام	نگاره	$\bar x$	$\bar y$	مساحت
مثلث راست‌گوشه		$\frac{-b}{3}$	$\frac{h}{3}$	$\frac{bh}{2}$
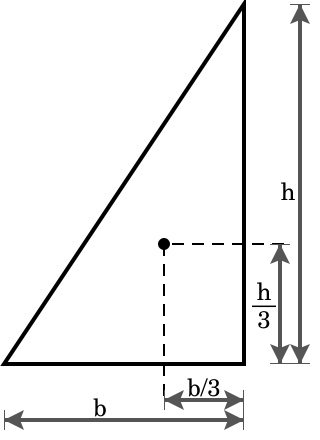
ربع دایره		$\frac{4r}{3\pi}$	$\frac{4r}{3\pi}$	$\frac{\pi r^2}{4}$
نیم‌دایره	\| align="center"\| $\,\!0$	$\frac{4r}{3\pi}$	$\frac{\pi r^2}{2}$
ربع بیضی	\| align="center"\| $\frac{4a}{3\pi}$	$\frac{4b}{3\pi}$	$\frac{\pi a b}{4}$
نیم‌بیضی		$\,\!0$	$\frac{4b}{3\pi}$	$\frac{\pi a b}{2}$
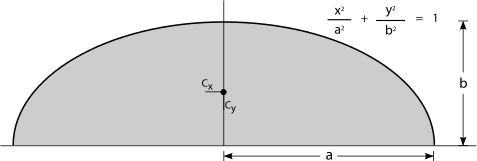
نیمه سهمی گون	The area between the curve $y = \frac{h}{b^2} x^2$ and the $\,\!y$ axis, from $\,\!x = 0$ to $\,\!x = b$	$\frac{3b}{8}$	$\frac{3h}{5}$	$\frac{2bh}{3}$
سهمی	The area between the curve $\,\!y = \frac{h}{b^2} x^2$ and the line $\,\!y = h$	$\,\!0$	$\frac{3h}{5}$	$\frac{4bh}{3}$
Parabolic spandrel	The area between the curve $\,\!y = \frac{h}{b^2} x^2$ and the $\,\!x$ axis, from $\,\!x = 0$ to $\,\!x = b$	$\frac{3b}{4}$	$\frac{3h}{10}$	$\frac{bh}{3}$
General spandrel	The area between the curve $y = \frac{h}{b^n} x^n$ and the $\,\!x$ axis, from $\,\!x = 0$ to $\,\!x = b$	$\frac{n + 1}{n + 2} b$	$\frac{n + 1}{4n + 2} h$	$\frac{bh}{n + 1}$
قاچ دایره	The area between the curve (in polar coordinates) $\,\!r = \rho$ and the pole, from $\,\!\theta = -\alpha$ to $\,\!\theta = \alpha$	$\frac{2\rho\sin(\alpha)}{3\alpha}$	$\,\!0$	$\,\!\alpha \rho^2$
قطاع دایره		$\,\!0$	$\frac{4R\sin^3{\frac{\theta}{2}}}{3(\theta-\sin{\theta})}$	$\frac{R^2}{2}(\theta -sin{\theta})$
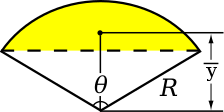
Quarter-circular arc	The points on the circle $\,\!x^2 + y^2 = r^2$ and in the first quadrant	$\frac{2r}{\pi}$	$\frac{2r}{\pi}$	$\frac{\pi r}{2}$
کمان نیم دایره	The points on the circle $\,\!x^2 + y^2 = r^2$ and above the $\,\!x$ axis	$\,\!0$	$\frac{2r}{\pi}$	$\,\!\pi r$
کمان دایره	The points on the curve (in polar coordinates) $\,\!r = \rho$ , from $\,\!\theta = -\alpha$ to $\,\!\theta = \alpha$	$\frac{\rho\sin(\alpha)}{\alpha}$	$\,\!0$	$\,\!2\alpha \rho$