الگوریتم کساراجو

الگوریتم کساراجو

کلاس	الگوریتم گراف
داده ساختار	گراف و پشته
بدترین زمان اجرا	$O(|E| + |V| )$

الگوریتم کساراجو الگوریتمی است که به منظور پیدا کردن مولفه های قویا همبند در یک گراف جهت دار. این الگوریتم توسط سامباسیوا کساراجو در سال ۱۹۷۸
در یک مقاله ارایه شد. کساراجو این الگوریتم را با استفاده از این نکته که مولفه‌های قویا همبند در یک گراف جهت‌دار با مولفه‌های قویا همبند در معکوس آن گراف جهت‌دار برابر هستند، ارایه کرد. الگوریتم دیگری که بر پایه همین الگوریتم است، الگوریتم تارجان است که در واقع نسخه‌ی بهبودیافته الگوریتم کساراجو است. در حدود ۲۰ سال بعد یعنی در سال ۱۹۹۶ نسخه‌ی بهبودیافته‌ی دیگری از این الگوریتم، توسط گابو منتشر شد.

مفاهیم

• گراف قویا همبند

به گرافی گویند که هر جفت راس آن از یکدیگر قابل دسترس باشد. مانند شکل زیر:

گراف قویا همبند

• مولفه قویا همبند:

مولفه قویا همبند یک گراف به بیشینه زیرمجموعه‌ای از راس ها گویند که قویا همبند هستند. یعنی از هر جفت راس در آن مجموعه به یکدیگر مسیر مستقیم وجود دارد. مانند شکل زیر:

مولفه های قویا همبند

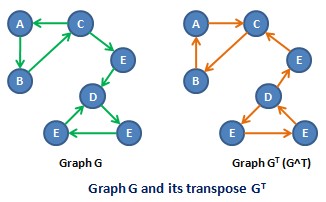
• گراف معکوس:

گراف معکوس یا همان G^T که در آن راس u به راس v یال دارد اگر و فقط اگر در گراف G راس v به راس u یال داشته باشد. یعنی مجموعه یال‌های آن به صورت زیر است:

{ E^T = { (u,v) | (v,u) ∈ E

مانند شکل زیر:

معکوس گراف

الگوریتم

این الگوریتم از یک نکته‌ی بسیار ساده استفاده می کند. این نکته که مولفه‌های قویا همبند یک گراف جهت‌دار با مولفه‌های قویا همبند معکوس آن گراف جهت‌دار یکی است، پایه‌ی اصلی این الگوریتم است.

ابتدا یک پشته خالی در نظر می گیریم . گراف جهت‌دار داده شده را، G در نظر می گیریم. این گراف را پیمایش می کنیم. پیمایش این گراف را از یک راس دلخواه به وسیله‌ی یکی از الگوریتم‌های پیمایش گراف یعنی جستجوی عمق اول انجام می دهیم. وقتی الگوریتم جستجوی عمق اول کار خود را با یک راس به اتمام رساند، آن را در داخل پشته قرار می دهیم. به همین ترتیب ادامه می دهیم تا کل گراف پیمایش شود.
در این مرحله تمامی راس ها در داخل پشته قرار دارند.
سپس گراف معکوس G یعنی G^T را به دست می‌آوریم.این بار گراف معکوس را با توجه به اولویت راس ها در پشته، پیمایش می‌کنیم. به این ترتیب که در ابتدا از راسی شروع می‌کنیم که در بالای پشته قرار دارد. فرض کنید راس v در بالای پشته است. جستجوی عمق اول را از آن راس شروع می کنیم. فرض کنید در راسی به نام w به پایان برسد. تمام راس‌هایی که در این بین ملاقات شده جزو یک مولفه‌های قویا همبند هستند. تمام راس های ملاقات شده را از پشته خارج و همین الگوریتم را بر روی راسی که در بالای پشته قرار دارد، تکرار می‌کنیم، تا زمانی که پشته خالی شود.

مثال

برای درک بیشتر الگوریتم مثال زیر را در نظر بگیرید. فرض کنید می خواهیم مولفه های قویا همبند را در گراف شکل زیر پیدا کنیم.

ابتدا گراف مورد نظر را با استفاده از الگوریتم جستجوی عمق اول با شروع از راس A پیمایش می‌کنیم.
مطابق آنجه در توضیح الگوریتم گفتیم بعد از اجرای جستجوی عمق اول بر روی گراف از راس A، راس H وارد پشته می شود. به این خاطر که جستجوی عمق اول در راس H متوقف می شود. بعد از آن، به ترتیب راس های F - E - C - G وارد پشته می شوند. سپس جستجوی عمق اول بار دیگر از A ادامه پیدا کرده و در انتها، پشته به صورت زیر پر می شود:
سر پشته --> [H, G, C, E, F, D, B, A]
پس از آن معکوس گراف را محاسبه می‌کنیم. معکوس گراف مورد نظر مطابق شکل زیر است:

حال مطابق آنچه در توضیح الگوریتم گفته شد، جستجوی عمق اول را بر روی گراف معکوس، با شروع از راسی که در سر پشته است (یعنی A)، اجرا می‌کنیم.با پیمایش گراف از راس A، تنها دو راس B و D ملاقات می شوند. بنابراین ۳ راس A و B و D، تشکیل یک مولفه‌ی قویا همبند می‌دهند. پس کافی است این ۳ راس را mark کرده (از پشته و گراف خارج کنیم) و الگوریتم را ادامه دهیم. راس F اکنون سر پشته است و قبلا ملاقات (mark) نشده است. پس الگوریتم جستجوی عمق اول را بر روی آن اجرا می‌کنیم و F و E را به عنوان یک مولفه‌ی قویا همبند دیگر، گزارش می کنیم. با ادامه الگوریتم H و G و C نیز که در پشته باقی مانده‌اند، به عنوان آخرین مولفه‌ی قویا همبند گزارش می کنیم.

اثبات درستی الگوریتم

در نگاهی عمیق‌تر به الگوریتم، می‌توان متوجه شد که هر چه یک راس در قسمت بالاتری از پشته قرار گیرد، به این معناست که در زمان دیرتری مراحل الگوریتم بر روی آن به پایان رسیده است . به بیان دیگر اگر (f(u زمان به پایان رسیدن مراحل جستجوی عمق اول بر روی راس u نظر گرفته شود، هر چه راس u در پشته بالاتر (به سر پشته نزدیک‌تر) باشد، دارای (f(u بزرگتری نیز است. برای به دست آوردن f مربوط به هر راس، کافی است الگوریتم جستجوی عمق اول را به صورت زیر تغییر دهیم:

Algorithm DFS(G)
1 for each vertex u ∈ V [G]
2    mark U as not visited  
3 time ← 0
4 for each vertex u ∈ V [G]
5   do if u is unvisited 
6     then DFS-Visit (u)   

Algorithm DFS-Visit(u) 
1 mark u as visited
2 d[u] ← time
3 time + 1
4 for each v ∈ Adj[u]
5    do if v is unvisited
6      then DFS-Visit (v)
7 f [u] ← time
8 time + 1

پس الگوریتم کساراجو در واقع به این صورت است که

• الگوریتم جستجوی عمق اول را بر روی گراف G اجرا می‌کند و (f(u را به ازای تمام راس‌ها بدست می‌آورد.(پشته در الگوریتم کساراجو نقش ترتیب نزولی (f(uها به ازای تمامی راس‌ها است)
• معکوس گراف G، یعنی G^T را محاسبه می‌کند.
• الگوریتم جستجوی عمق اول را بر روی G^T اجرا می‌کند ولی راس‌ها را با اولویت (f(u با ترتیب نزولی در نظر می‌گیرد ( همان ترتیب راس‌ها در پشته )
• راس‌ها را در هر درخت حاصل از جستجوی عمق اول به عنوان یک مولفه قویا همبند (SCC) چاپ می‌کند.

تعریف

به ازای هر زیر مجموعه‌ای از راس‌ها مانند U  :

f(U) = max _u∈U { f(u) }

لم

فرض کنید C₁ و C₂ دو مولفه متمایز قویا همبند در گراف G باشند و وجود دارد یک یالی از راس u به راس v به طوری که u ∈ C₁ و v ∈ C₂ در این صورت (f(C₁ بزرگتر از (f(C₂ است. اثبات: دو حالت وجود دارد:

• ابتدا C₁ توسط الگوریتم جستجوی عمق اول ملاقات شود:

در ابتدا تمامی راس‌های موجود در C₁ ملاقات شده و سپس از طریق یال u به v، راس‌های C₂ ملاقات می‌شوند. چون C₂ یالی به خارج از خود ندارد پس در ابتدا راس های آن به پایان می رسد و سپس راس‌های C1 به پایان می‌رسد.

• ابتدا C₂ توسط الگوریتم جستجوی عمق اول ملاقات شود

در ابتدا تمامی راس‌های موجود در C₂ ملاقات شده و چون C₂ یالی به خارج از خود ندارد پس الگوریتم در همان مولفه به پایان می رسد. سپس با شروع از راس‌های C₁ به کار خود ادامه می‌دهد.
بنابراین در هر دو حالت (f(C₁ بزرگتر از (f(C₂ خواهد بود.

مولفه‌های همبندی C1 و C2

نتیجه

یک نتیجه حاصل از این لم، این است که اگر در گراف G، داشته باشیم (f(C₁ بزرگتر از (f(C₂، در گراف معکوس یعنی G^T، برعکس خواهد بود و (f(C₁ کوچکتر از (f(C₂ خواهد بود. چون مولفه‌های قویا همبند در G و G^T برابر هستند و تنها جهت یال‌ها عوض خواهد شد.
بنابراین چون این الگوریتم در ابتدا (f(uها را محاسبه می‌کند و سپس در G^T، الگوریتم جستجوی عمق اول را از راسی که بیشینه (f(u را در گراف G دارد، اجرا می‌کند، این راس یعنی u مطابق نتیجه‌ای که در بالا گرفته شد، دارای کمینه (f(u است.
به این ترتیب، اگر مولفه‌ای که u در آن وجود دارد را C₃ بنامیم، الگوریتم جستجوی عمق اول در ابتدا تمامی همسایگان u را در C₃ ملاقات می کند. حال ادعا می‌کنیم که جستجوی عمق اول در این مرحله به پایان می‌رسد. چون در غیر این صورت باید از C3 به یکی دیگر از مولفه‌ها مانند Ci یال وجود داشته باشد. درحالیکه از C₃ به هیچ مولفه دیگری مانند Ci، یال وجود ندارد. چون اگر یالی از یک راس در C₃ به یک راس در مولفه دیگر مانند C_i وجود داشت، طبق لم بالا، (f(C₃ از (f(C_i بزرگتر بود که این با کمینه بودن (f(C₃ تناقض است. بنابراین الگوریتم به درستی اولین مولفه قویا همبند را مشخص کرد. در مرحله بعد (f(C_i به گونه‌ای انتخاب می شود که در گراف G، از (f(C مربوط به تمامی مولفه‌ها به جز (f(C₃ بزرگتر است. به این ترتیب الگوریتم به درستی کار خود را به پایان می‌برد.

تحلیل زمانی

همان طور که در توضیح الگوریتم گفته شد، الگوریتم شامل ۳ مرحله است:

• پیمایش گراف و پر کردن پشته
• معکوس کردن گراف
• پیمایش گراف با توجه به اولویت راس‌ها با استفاده از پشته

در صورتی که گراف به وسیله ماتریس مجاورت پیاده سازی شود، زمان اجرای این الگوریتم از (^۲|O(|V خواهد بود.
از طرف دیگر می‌دانیم اگر گراف به وسیله لیست مجاورت پیاده سازی شود، الگوریتم جستجوی عمق اول به زمان (|O(|V|+|E نیاز دارد که در آن V تعداد راسها و E تعداد یال هاست. برای معکوس کردن گراف نیز کافی است یک بار گراف را به وسیله جستجوی اول عمق پیمایش کرده و در گذر از هر یال جهت آن یال را عوض کنیم. پس آن نیز به (|O(|V|+|E زمان نیاز دارد.
پس در کل ۳ بار جستجوی اول عمق نیاز داریم .می توان مرحله اول و مرحله معکوس کردن را در یک بار پیمایش گراف انجام دهیم به این ترتیب تنها به دو جستجوی اول عمق نیاز داریم پس در کل زمان اجرا برابر(|O(|V|+|E است.

پیاده سازی

شبه‌کد الگوریتم کساراجو به صورت زیر است:

 1  Algorithm  Kosaraju(G,v)
 2  Input : G=(V,E),)
 3  Output : strongly connected component (SCC)
 4  begin
 5      while(stack does not contain all vertices)
 6         Choose an arbitrary vertex v not in S
 7         Depth First Search(G,V)
 8         Each time that depth-first search finishes expanding a vertex u, push u onto S
 9      compute GT
10      While(stack is not empty)
11           pop vertex v form stack
12           Depth First Search(GT,v)
13           Output set of visited vertices as a seprate SCC 
14           mark this set of vertices form stack and graph 
12  end

پیاده‌سازی الگوریتم با استفاده از جاوا:

import java.util.ArrayList;
 
public class Kosaraju {
 
   private ArrayList<Node> stack;
 
   public ArrayList<ArrayList<Node>> getSCC(Node root, AdjacencyList list){
       stack = new ArrayList<Node>();
 
       // search the graph (depth-first search), adding nodes to the stack
       search(root, list, true);
 
       // reverse all the edges in the graph
       list.reverseGraph();
 
       // search the graph again in the stack's order
       ArrayList<ArrayList<Node>> SCC = new ArrayList<ArrayList<Node>>();
       while(!stack.isEmpty()){
           ArrayList<Node> component = new ArrayList<Node>();
           search(stack.get(0), list, false);
 
           // any components we visited are strongly connected
           // remove them from the stack and add them to the component
           for(Iterator<Node> it = stack.iterator(); it.hasNext(); ){
               Node n = it.next();
               if(!n.visited){
                   component.add(n);
                   it.remove();
               }
           }
 
           // add the component to the result set
           SCC.add(component);
       }
       return SCC;
   }
 
   private void search(Node root, AdjacencyList list, boolean forward){
       root.visited = forward;
       if(list.getAdjacent(root) == null){
           if(forward) stack.add(0, root);
           return;
       }
       for(Edge e : list.getAdjacent(root)){
           if(e.to.visited != forward){
               search(e.to, list, forward);
           }
       }
       if(forward) stack.add(0, root);
   }
}

کاربرد

پیدا کردن مولفه‌های قویا همبند از مهمترین مسایل در نظریه گراف است. با بدست آوردن گراف مولفه‌های قویا همبند، بسیاری از مسایل نظریه گراف به راحتی قابل حل است. مانند:

• به دست آوردن راس برشی
• به دست آوردن یال برشی
• به دست آوردن تور اویلر

که همه این مسایل با داشتن گراف مولفه‌های قویا همبند، در (|O(|E قابل حل است.
علاوه بر این مساله مولفه‌های قویا همبند در مخابرات و شبکه نیز بسیار کاربرد دارد.

جستار های وابسته

• گراف همبند
• پیمایش گراف
• تجزیه گراف به مؤلفه‌های دوهمبند و قویا همبند

منابع

• http://scienceblogs.com/goodmath/2007/10/computing_strongly_connected_c.php
• http://lcm.csa.iisc.ernet.in/dsa/node171.html#fig:strong2
• http://www.cs.huji.ac.il/course/2003/dast/lectures/lect14.pdf

پیوند به بیرون

• الگوریتم کساراجو به همراه توضیحات و شبه کد
• کساراجو به همراه توضیحات و اثبات
• m پیاده‌سازی الگوریتم به زبان جاوا
• j توضیح الگوریتم به همراه شبه‌کد و اثبات

در ویکی‌انبار پرونده‌هایی دربارهٔ الگوریتم کساراجو موجود است.