الگوریتم ساختمان تامپسون
در علوم نظری کامپیوتر ، به ویژه در نظریه زبان رسمی ، الگوریتم ساختمان تامپسون (TCA) یک عبارت منظم را به یک اتوماتای قطعی متناهی (NFA) تبدیل میکند، که یک تبدیل بین دو نوع از چند نوع فرمت تعریف زبانهای منظم ایجاد میکند. هنگامی که عبارتهای منظم به عنوان مثال برای توصیف الگوهای جستجوی پیشرفته در عملیاتهایی شبیه "پیدا و جایگزین کردن" در خدمات پردازش متن مورد استفاده قرار میگیرند، فرم NFA برای اجرا روی کامپیوتر مناسب تر است.
الگوریتم به صورت بازگشتی کار میکند به این صورت که با قطعه قطعه کردن عبارت به زیرعبارتهای اصلی ، و با استفاده از یک سری قوانین، NFA ساخته میشود.[۱] چنین اتوماتایی میتواند با ساختمان پاورست و بعد مینیمم سازی آن با هدف تولید اتوماتایی بهینه ، به یک اتوماتای قطعی متناظر با عبارت منظم داده شده تبدیل شود.
برعکس الگوریتم تامپسون ، الگوریتم کلین یک اتوماتای متناهی را به یک عبارت منظم تبدیل میکند.
قوانین
[ویرایش]قوانینی که در ادامه می آیند مطابق با (Aho et al(1986 ، [۲] صفحه 122 شرح داده شدهاند. (N(s و (N(t به ترتیب NFA زیر عبارتهای s و t میباشند.
- یک عبارت تهی ε تبدیل میشود به
- یک نماد a از الفبای ورودی تبدیل میشود به
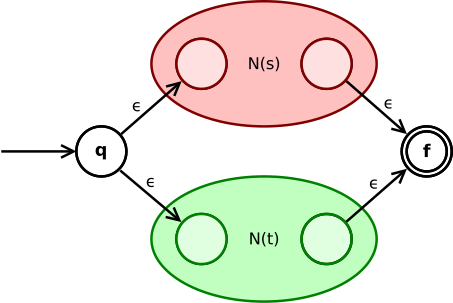
- عبارت اجتماع s|t تبدیل میشود به
وضعیت q با ε به وضعیتهای شروع (N(s یا (N(t میرود. وضعیتهای پایانی آنها تبدیل به وضعیتهای واسطه NFA کل میشوند و با دو انتقال ε به وضعیت پایانی NFA میروند.
- عبارت الحاق st تبدیل میشود به
وضعیت شروع (N(s تبدیل به وضعیت شروع NFA کل میشود. وضعیت پایانی (N(s تبدیل به وضعیت شروع (N(t میشود. وضعیت پایانی (N(t تبدیل به وضعیت پایانی NFA کل میشود.
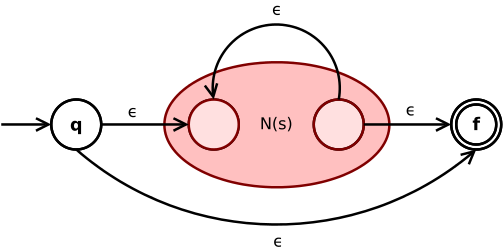
- عبارت ستاره کلین s* تبدیل میشود به
یک انتقال ε عبارتهای شروع و پایان NFA با زیر-NFA (N(s در وسط ، آنها را به هم وصل میکند. یک انتقال ε دیگر نیز از وضعیت پایانی داخلی به وضعیت شروع داخلی (N(s ، تکرار عبارت s را با توجه به عملگر ستاره را ممکن میسازد.
- عبارت پرانتزگذاری شده (s) به خود (N(s تبدیل میشود.
یک الگوریتم نیز قبل از این توسط McNaughton و Yamada معرفی شده بود.[۳]
مثال
[ویرایش]
(0|(1(01*(00)*0)*1)*)*
به عنوان یک مثال ، تصویر نتیجه الگوریتم ساخت تامپسون را بر روی عبارت منظم(0|(1(01*(00)*0)*1)*)* که مجموعه اعداد دودویی بخش پذیر بر ۳ را نمایش میدهد:
{ ε, "0", "00", "11", "000", "011", "110", "0000", "0011", "0110", "1001", "1100", "1111", "00000", ... }.بخش بالا سمت راست ساختار منطقی (درخت سینتکس) عبارت را نشان میدهد ، که در آن الحاق با "." نشان داده شده (فرض شده که آرگومان متغیر دارد). زیرعبارتها برای مقاصد ارجاع با a-q نامگذاری شدهاند. بخش چپ اتوماتای متناهی منطقی بدست آمده از الگوریتم تامپسون را نشان میدهد. وضعیت ورودی یا خروجی هر زیرعبارت به ترتیب با رنگ ارغوانی و فیروزهای نشان داده شدهاست. از نماد ε به عنوان نماد انتقال برای وضوح بیشتر صرف نظر شدهاست. انتقالهای بدون برچسب در واقع همان انتقالهای ε هستند. وضعیت ورودی و خروجی متناظر با ریشه عبارت q به ترتیب وضعیت شروع و پذیرش اتوماتا است.
گامهای الگوریتم به شرح زیر میباشد:
| q: | شروع تبدیل عبارت ستاره کلین | (0|(1(01*(00)*0)*1)*)*
| ||||||||
| b: | شروع عبارت اجتماع | 0|(1(01*(00)*0)*1)*
| ||||||||
| a: | نماد تبدیل | 0
| ||||||||
| p: | شروع تبدیل عبارت ستاره کلین | (1(01*(00)*0)*1)*
| ||||||||
| d: | شروع تبدیل عبارت الحاق | 1(01*(00)*0)*1
| ||||||||
| c: | نماد تبدیل | 1
| ||||||||
| n: | شروع تبدیل عبارت ستاره کلین | (01*(00)*0)*
| ||||||||
| f: | شروع تبدیل عبارت الحاق | 01*(00)*0
| ||||||||
| e: | نماد تبدیل | 0
| ||||||||
| h: | شروع تبدیل عبارت ستاره کلین | 1*
| ||||||||
| g: | نماد تبدیل | 1
| ||||||||
| h: | پایان تبدیل عبارت ستاره کلین | 1*
| ||||||||
| l: | شروع تبدیل عبارت ستاره کلین | (00)*
| ||||||||
| j: | شروع تبدیل عبارت الحاق | 00
| ||||||||
| i: | نماد تبدیل | 0
| ||||||||
| k: | نماد تبدیل | 0
| ||||||||
| j: | پایان تبدیل عبارت الحاق | 00
| ||||||||
| l: | پایان تبدیل عبارت ستاره کلین | (00)*
| ||||||||
| m: | نماد تبدیل | 0
| ||||||||
| f: | پایان تبدیل عبارت الحاق | 01*(00)*0
| ||||||||
| n: | پایان تبدیل عبارت ستاره کلین | (01*(00)*0)*
| ||||||||
| o: | نماد تبدیل | 1
| ||||||||
| d: | پایان تبدیل عبارت الحاق | 1(01*(00)*0)*1
| ||||||||
| p: | پایان تبدیل عبارت ستاره کلین | (1(01*(00)*0)*1)*
| ||||||||
| b: | fپایان تبدیل عبارت اجتماع | 0|(1(01*(00)*0)*1)*
| ||||||||
| q: | پایان تبدیل عبارت ستاره کلین | (0|(1(01*(00)*0)*1)*)*
| ||||||||
یک اتوماتای قطعی مینیمال شده در شکل زیر نشان داده شدهاست.

منابع
[ویرایش]- مشارکتکنندگان ویکیپدیا. «Thompson's construction algorithm». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۸ فوریه ۲۰۱۵.
- ↑ Ken Thompson (Jun 1968). "Programming Techniques: Regular expression search algorithm". Communications of the ACM. 11 (6): 419–422. doi:10.1145/363347.363387.
- ↑ Alfred V. Aho, Ravi Sethi, Jeffrey Ullman: Compilers: Principles, Techniques and Tools. Addison Wesley, 1986
- ↑ R. McNaughton, H. Yamada (Mar 1960). "Regular Expressions and State Graphs for Automata". IEEE Trans. on Electronic Computers. 9 (1): 39–47. doi:10.1109/TEC.1960.5221603.