هرم دودویی
هرم دودویی یک دادهساختار هرم است که از یک درخت دودویی استفاده میکند. میتوان به این دادهساختار به عنوان یک درخت دودویی نگاه کرد با این تفاوت که باید دو محدودیت را در نظر بگیریم. اول اینکهای درخت، درخت دودویی کامل است، در همهٔ سطحهای این درخت این ویژگی برقرار است به جز احتمالاً سطح اخر که در سطح اخر گرهها از چپ به راست پر هستند (خاصیت ظاهری). و مورد دوم اینکه همه گرهها از فرزندشان کوچکترمساوی (یا بزرگترمساوی) هستند. اگر همه گرهها از فرزندانشان کوچکترمساوی باشند هرم کمینه و اگر همه گرهها بزرگترمساوی از فرزندانشان باشند هرم بیشینه نامگذاری میشوند (خاصیت هرم). اغلب برای پیادهسازی صف اولویت از هرم کمینه استفاده میشود.
به این دلیل اینکه ترتیب فرزندان در هرم بهطورمشخص نیست میتوان جای آنها را عوض کرد مگراینکه خاصیت ظاهری نقض شود.
عملگرهای هرم[ویرایش]
هردو عمل درج و حذف در هرم دودویی در زمان (O(log n انجام میشود.
درج[ویرایش]
برای درج کردن الگوریتم به صورت زیر است:
- اضافه کردن عنصر جدید به سطح پایین هرم
- عنصر اضافه شده را با پدرش مقایسه کنید، اگر ترتیب آنها درست بود الگوریتم متوقف میشود
- درغیراینصورت جای آن را با پدرش عوض میکنیم و سپس مرحله قبلی را تکرار میکنیم.
تعداد عملیات مورد نیاز به تعداد سطحهایی که عنصر جدید برای پیدا کردن مکان مناسب برای ارضا کردن ویژگی هرم باید طی کند بستگی دارد به همین دلیل بهطور متوسط این عملیات در زمان (O(log n انجام میشود.
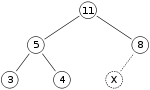
به عنوان مثال یک هرم بیشینه را در نظر بگیریم:
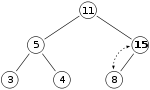
حال میخواهیم گره با کلید ۱۵ را درج کنیم:
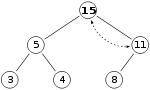
با توجه به اینکه هنوز ویژگی هرم بیشینه رعایت نشدهاست باید جای جای ریشه با فرزند سمت راست عوض کرد.
حذف[ویرایش]
روش حذف کردن ریشه هرم و بازسازی هرم به منظور حفظ ویژگی آن پایین-هرم نامیده میشود که این روش به صورت زیر است:
- ریشه هرم را با آخرین عنصر آخرین سطح جابهجا کنید
- مقایسه کنید ریشه را با فرزندانش اگر ویژگی هرم برقرار بود الگوریتم متوقف میشود
- در غیراینصورت جای ان را با فرزندانش عوض کنید و مرحله قبلی را تکرار کنید.
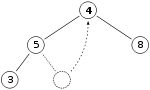
به عنوان مثال میخواهیم گره با کلید ۱۱ را حذف کنیم:
۱۱ را حذف میکنیم و با ۴ جابهجا میکنیم
حال مرحله ۳ الگوریتم را انجام میدهیم
در بدترین حالت ریشه جدید باید تا پایینترین سطح بیاید تا ویژگی هرم برقرار شود، این جمله معنی میدهد که عملیات حذف با ارتفاع درخت رابطه دارد که بهطور متوسط (O(log n است.
ایجاد[ویرایش]
یک هرم میتواند با درجهای متوالی ساخته شود. پیچیدگی زمانی این کار (O(n log n، زیرا هر درج در زمان (O(log n صورت میگرد وعمل درج n با انجام میشود، اما این روش بهینه نیست. روش بهینه با قرار دادن عناصر به صروت دلخواه در یک درخت دودویی شروع میشود سپس از پایینترین سطح شروع میکند و به سمت بالا حرکت میکند. ریشه هر زیردرخت رو به پایین را حرکت میدهد تا ویژگی هرم بازیابی شود. به دلیل اینکه ارتفاع درخت است، درست کردن ویژگی هرم همهٔ زیردرختها برابر است با:
که مقدار واقعی عبارت بالا برابر است با:
- ،[۱]
که (s2(n برابر است با جمع همهٔ رقمهای نمایندههای دودویی n و (e2(n توان دو در فاکتوگیری اول n است. تابع ساختن هرمبیشینه یک آرایه را به یک درخت دودویی که هرم بیشینه هست تبدیل میکند و از تابع Max-Heapify استفاده میکند. شبه کد به صورت زیر است:
Build-Max-Heap (A)
heap_length[A] ← length[A]
for i ← floor(length[A]/2) downto 1 do
Max-Heapify(A, i)
پیادهسازی هرم[ویرایش]


هرمها بهطور رایج با آرایه پیادهسازی میشوند. یک درخت دودویی میتواند در یک آرایه ذخیره شود. هیچ فضایی برای اشارهگر نیاز نیست، درعوض گره فرزندان و پدر به وسیلهٔ حساب کردن شاخصهای آرایه پیدا میشوند. با این ویژگی پیادهسازی هرم به صورت ساده انجام میشود. جزییات به موقعیت ریشه بستگی دارد که به نوبه خود به محدودیت زبان برنامهنویسی مورد استفاده برای پیادهسازی بستگی دارد. بهطور خاصتر بعضی اوقات ریشه در مکان ۱ قرار میگیرد. n را تعداد عناصر هرم در نظر بگبرید و i را هم مقدار دلخواه اندیس آرایه، اگر ریشه را در اندیس صفر قرار دهیم انگاه اندیس هر عنصر به صورت زیر میشود:
- فرزندان و
- پدرشان
اگر ریشه در اندیس ۱ قرار بگیرد، اندیس هر عنصر به صورت زیر میشود:
- فرزندان و
- پدرشان
این پیادهسازی همچنین برای استفاده به عنوان صف اولویت مناسب است. عملیات هرمبالا/هرمپایین میتواند در شرایط یک آرایه به صورت زیر اعلام شود: فرض کنید که ویژگی هرم نگه میدارد برای مشخصههای b, b+1, ... , e. تابع غربال کردن به پایین ویژگی هرم را بهb−1, b, b+1, ... , e گسترش میدهد، فقط اندیس i = b−۱ میتواند این ویژگی را نقض کند. فرض کنید اندیس j بزرگترین بچه[ a[i در هرم بیشینه (کوچکترین فرزند در درخت کمینه) باشد. با جابهجا کردن [a[i و [a[j ویژگی هرم برای اندیس i برقرار میشود. در این مرحله تنها مسیله این است که ویژگی هرم برای اندیس j برقرار نباشد. تابع غربال کردن به پایین عملی میکنددم-بازگشتیرا تا برای همه عناصر ویژگی هرم برقرار باشد.
تابع غربال کردن به پایین سریع عمل میکند. در هر مرحله فقط به دو مقایسه و یک جابهجایی نیاز دارد. مقدار شاخص در هر تکرار دوبرابر کار میکند، بهطوریکه تعداد مراحل حداکثر برابر است باlog2 e
برای یک هرم بزرگ و استفاده کردن از حافظه مجازی ذخیره کردن در آرایه به صورت بالا ناکارآمد است.(تقریباً) هر سطر که در یک صفحه (حافظه کامپیوتر) متفاوت است، هرمهای دودویی هستند که زیردرختها را در یک حافظه منفرد نگه میدارند، تعداد حافظههای قابل دسترسی به بالا از عامل ده را کاهش میدهد.[۲]
عمل ادغام دو هرم دودویی در (Θ(n صورت میگیرد که n اندازه هرم است. بهتر است که شما بهطور ساده دو آرایه هرم را ادغام کنید و سپس از حاصل یک هرم دودویی بسازید.[۳] یک هرم با n عنصر و یک هرم با k عنصر میتوانند در (O(log n log k با هم ادغام شوند..[۴] یک الگوریتم برای جداکردن یک هرم دودویی با n عنصر و تبدیل به دو هرم دودویی با n-k عنصر k عنصر، بهترتیب، براساس یک دیدگاه جدید هرم به عنوان مجموعه مرتبشده زیرهرم ارائه شد.[۵] این الگوریتم به (O(log n * log n مقایسه نیاز دارد. این دیدگاه جدید همچنین بهطور مفهومی الگوریتم ساده برای ادغام دو هرم ارائه میدهد. وقتی که ادغام یک کار رایج است، پیادهسازی یک هرم متفاوت توصیه میشود، مانند هرم دوجملهای که در (O(log n ادغام میشود.
به علاوه یک هرم دودویی میتواند با یک دادهساختار درخت دودویی مرسوم پیادهسازی شود، اما یک نکته برای پیدا کردن عنصر مجاور آخرین سطح روی هرم دودویی وجود دارد. این عنصر میتواند به صورت الگوریتمی پیدا شود یا با اضافه کردن اصلاعات اضافی به گرههاکه نخ نامیده میشود مانند اضافه کردن یک فیلد بعدی به هر گره پیدا شود. میتوان با اصلاح ساختار هرم هر دو عنصر کوچکترین و بزرگترین در (O(log n پیدا کرد.[۶] برای اینکار ردیفهای متاوب بین هرم بیشینه و کمینه را جایگزین میکنیم. این الگوریتمها تقریباً متاوب هستند، اما در هر مرحله باید ردیفهای متاوب را با مقایسههای متناوب در نظر بگیریم. کارایی این الگوریتم تقریباً مشابه جهت منفرد طبیعی هرم است. این ایده میتواند برای هرم-بیشینه-کمینه-میانه تعمیم پیذا کند.
اشتقاق معادلات شاخص[ویرایش]
در یک آرایه هرم، پدر و فرزندان میتوانند با یک حساب ساده روی مشخصه (اندیس) آرایه پیدا شوند. در این بخش به بررسی معدلات مشتق شده هرم وقتی که اندیس ریشه در آرایه صفر است و یادداشتهایی وقتی اندیس ریشه در آرایه یک است را میپردازیم.
برای جلوگیری از ابهام، سطح را فاصله از ریشه معنی میکنیم، بهطوریکه خود ریشه در سطح صفر هست.
گرههای فرزندان[ویرایش]
بهطور عمومی گره که در اندیس i هست، فرزند سمت راست ان در اندیس2i+۲ هست.
گره i را در سطح L در نظر بگیرید، و توجه کنید که هر سطح l دقیقاً گره شمامل میشود. به علاوه دقیقاً گره در لایههای بالایی شامل میشوند. به دلیل اینکه ریشه در اندیس صفر هست k امین گره در اندیس ذخیره میشود. این مشاهدات را برای نتیجه در کنار هم قرار میدهیم تا عبارت زیر برای اندیس اخرین عنصر در لایه l بدست بیاید
j را گرههای بعد از گره i در نظر بگیرید، بهطوری که:
هر کدام از گرههای j باید دقیقاً دو فرزند داشته باشند، بنابراین باید وجود داشته باشد گره برای جداسازی 's فرزند راست از انتهای خودش لایه ()
به عنوان مورد نیاز.
توجه کنید که فرزند سمت چپ یک گره یک مکان قبل تر از فرزند سمت راست است بنابراین: .
اگر ریشه به جای اندیس صفر در اندیس یک باشد، اندیس آخرین گره در هر سطح برابر است با . همچنین با استفاده از مطالب ذکر شده برای یک هرم با اندیس یک ریشه و .
گره پدر[ویرایش]
هر گره یا فرزند سمت چپ یا فرزند سمت راست پدر خودش هست، بنابراین:
در نتیجه:
حال عبارت را در نظر بگیرید.
اگر گره i فرزند سمت چپ باشد، بهطور بدیهی این نتیجه بدست میاید، اگرچه، اگر گره i فرزند راست باشد این نتیجه درست است. در این مورد، باید زوج باشد بنابراین باید فرد باشد.
بنابراین، با صرفنظر از اینکه گره i فرزند سمت راست یا چپ است، پدر این گره با عبارت زیر حساب میشود:
مین-هیپ[ویرایش]
مین-هیپ (به انگلیسی: min-heap) دارای ویژگی مین-هیپ است. در واقع برای هر گره به جز ریشه، رابطهٔ زیر صدق میکند:
کوچکترین عضو هرم در ریشه قرار دارد. برای الگوریتم مرتبسازی هرمی از مکس هیپ استفاده میشود. مین هیپ معمولاً برای صفهای اولویت مورد استفاده قرار میگیرد.

جستارهای وابسته[ویرایش]
منابع[ویرایش]
- T. Cormen (۱۰ نوامبر ۲۰۱۱)، Introduction to Algorithms، MIT Press، ص. ۱۵۲-۱۵۳ تاریخ وارد شده در
|تاریخ=را بررسی کنید (کمک)
- ↑ Suchenek, Marek A. (2012), "Elementary Yet Precise Worst-Case Analysis of Floyd's Heap-Construction Program", Fundamenta Informaticae, IOS Press, 120 (1): 75–92, doi:10.3233/FI-2012-751.
- ↑ Poul-Henning Kamp. "You're Doing It Wrong". ACM Queue. June 11, 2010.
- ↑ Chris L. Kuszmaul. "binary heap" بایگانیشده در ۸ اوت ۲۰۰۸ توسط Wayback Machine Dictionary of Algorithms and Data Structures, Paul E. Black, ed. , U.S. National Institute of Standards and Technology. 16 November 2009.
- ↑ J. -R. Sack and T. Strothotte "An Algorithm for Merging Heaps"[پیوند مرده], Acta Informatica 22, 171-186 (1985).
- ↑ . J. -R. Sack and T. Strothotte "A characterization of heaps and its applications" Information and Computation Volume 86, Issue 1, May 1990, Pages 69–86.
- ↑ Atkinson, M.D. , J. -R. Sack, N. Santoro, and T. Strothotte (1 October 1986). "Min-max heaps and generalized priority queues" (PDF). Programming techniques and Data structures. Comm. ACM, 29(10): 996–1000. Archived from the original (PDF) on 27 January 2007. Retrieved 1 February 2014.
{{cite web}}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link)































![{\displaystyle A[Parent(i)]<=A[i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30db07ca1da9197dbed9c5469498f0d5933ad49e)