الگوریتم اسمیت واترمن
الگوریتم اسمیت واترمن (به انگلیسی: Smith–Waterman algorithm) برای انجام دادن یک همترازسازی توالی محلی به کار گرفته میشود و برای مشخص کردن مناطق مشابه بین دو توالی اسید نوکلئیک یا پروتین استفاده میشود. به جای در نظر گرفتن تمام توالی این الگوریتم سعی میکند که با در نظر گرفتن بخشهای مختلف با همهٔ طولهای ممکن میزان شباهت را بهینه کند.
پیشینه
[ویرایش]این الگوریتم برای اولین با توسط تمپل اف. اسمیت و مایکل اس. واترمن در سال ۱۹۸۱ ارائه شد؛ که مانندالگوریتم نیدلمن-وانچ با یک سری تفاوتها یک الگوریتم برنامهریزی پویا میباشد. این الگوریتم دارای این خصوصیت است که بر حسب سیستم امتیاز دهی (شامل ماتریس جایگزنی و جریمه پرش) که استفاده میشود تضمین میکند که به جواب بهینه برسد. تفاوتی که با الگوریتم نیدلمن-وانچ دارد این است که در ماتریس جایگذاری آن مقادیر منفی با صفر جابگزین میشوند. عمل برگشت به عقب در این الگوریتم از خانه ایی که مقدار بیشنه را دارد شروع شده و به خانه ایی که مقدار صفر دارد ختم میشود؛ که این مسیر بیشترن امتیاز همترازسازی محلی را دارد.[۱]
انگیزه
[ویرایش]در سالهای اخیر پروژههای ژنومی که بر روی انواع مختلفی از جانداران انجام شدهاست، مقادیر بسیاری از دادههای توالی را برای ژنها و پروتئینها تولید میکند که نیاز به تجزیه و تحلیل محاسباتی دارد. همترازسازی توالی رابطه میان ژنها و یا پروتئینها را نمایش میدهد و منجر به درک بهتر از همسانی و عملکرد آنها می شود. همترازسازی توالی می تواند دامنهها و نقوش حفاظت شده را نیز نشان دهد.
یکی از انگیزههای همترازی محلی، دشواری دستیابی به تراز صحیح در مناطقی با شباهت کم بین توالی بیولوژیکی با مسافت کم است، زیرا جهش ها اختلالات زیادی را در طول زمان تکاملی اضافه کرده اند. همترازی محلی از چنین مناطقی کاملاً اجتناب می کند و به آنهایی که دارای نمره مثبت هستند، یعنی آنهایی که از نظر تحول تکاملی مشابه هستند ، متمرکز می شود. پیشنیاز همترازی محلی نمره انتظار منفی است. نمره انتظار به عنوان میانگین نمره ای تعریف می شود که سیستم امتیاز دهی (ماتریس جایگزنی و جریمه پرش) برای یک توالی تصادفی به دست می آورد.
انگیزه دیگر برای استفاده از ترازهای محلی این است که یک مدل آماری قابل اعتماد برای ترازهای محلی بهینه وجود دارد. همترازی توالیهای غیر مرتبط تمایل به تولید نمرات بهینه محلی دارد که از توزیع ارزش شدید پیروی می کنند. این ویژگی به برنامهها امکان می دهد که مقدار چشمداشتی (به انگلیسی: Expected value) را برای همترازی محلی مطلوب دو دنباله تولید کنند. این یک معیار است که چندوقت یکبار دو دنباله نامرتبط باعث همترازی محلی بهینه می شوند که نمره آن بزرگتر یا مساوی با نمره مشاهده شده باشد. مقدار چشمداشتی بسیار پایین نشان می دهد که این دو توالی مورد بحث ممکن است همگن باشند، به این معنی که ممکن است یک جد مشترک داشته باشند.
شرح الگوریتم
[ویرایش]مانند همه برنامهریزیهای پویا یک ماتریس را باید پر کنیم. ماترییس به اینصورت ساخته میشود.
که:
- = رشتههایی روی الفبا
- - مقدار بیشینه امتیاز شباهت یک پسوند [a[1...i و یک پسوند [b[1...j
- , که '-' نمایش جریمه پرش است
ماتریس تعویض
[ویرایش]ماتریس تعویض نشاندهنده این است که هر جابجایی میان نوکلئوتیدها (در ژنوم) یا اسید آمینهها در پروتئینها چه تاثیری در میزان شباهت رشتههای مورد بررسی دارند. در اینجا ما به بررسی یک ماتریس تعویض معروف و پرکاربر در هرکدام از توالییابی ژنومها یا پروتئینها میپردازیم:
ماتریس تعویض در ژنوم
[ویرایش]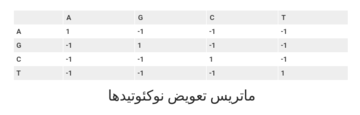
بهطور کلی همانطور که مشاهده میکنید برای تطابق امتیاز مثبت برابر با 1 و برای عدمتطابق امتیاز منفی برابر با -1 در نظر گرفته میشود. اصولا در نوکلئوتیدها تفاوتی میان انواع تطبیقناپذیریها قائل نمیشویم.
ماتریس تعویض در پروتئین
[ویرایش]برای پروتئینها ما از ماتریس تعویض بلوسام بهره میبریم. خواص این ماتریس عبارتند از:
- باتوجه با دادههای زیستی جمعآوری شده است.
- با استفاده از اعمال روشهای آماری بر بلوکهای آمینواسیدهای مشابه برای بدست آوردن امتیازهای شباهت بدست میآیند.
انواع متفاوتی از این ماتریسها وجود دارد که بنابر درصد تفاوت توالیهایی که در تشکیل این ماتریسها مورد بررسی قرار گرفته شده است نامگذاری میشوند ما در اینجا از BLOSUM62 استفاده میکنیم.[۲]

پیادهسازی به زبان پایتون
[ویرایش]import itertools as itr
import numpy as np
def score_matrix(v, u , match_score = 2, gap = 1):
matrix = np.zeros(len(v) + 1, len(u) + 1), np.init)
for i,j in itr,product((range(1, matrix.shape[0]), range(1, matrix.shape[1])):
match = matrix[i - 1, j - 1] + (match_score if v[i - 1] == u[j - 1] else - match_score)
delete = matrix[i - 1, j] - gap
insert = matrix[i, j - 1] - gap
matrix[i, j] = max(match, delete, insert, 0)
return matrix
def backtrack(smatrix, u, backtrace , prev):
smatrix_reversed = np.flip(np.flip(smatrix, 0), 1)
i_, j_ = np.unravel_index(smatrix_reversed.argmax(), smatrix_reversed.shape)
i, j = np.subtract(smatrix.shape, (i_ + 1, j_ + 1))
if smatrix[i, j] == 0:
return backtrace, j
backtrace = u[j - 1] + '-' + backtrace if prev - i > 1 else u[j - 1] + backtrace
return backtrack(smatrix=smatrix[0:i,0:j], u=u, backtrace=backtrace, prev=prev=)
def smith_waterman(v, u, match_score=2, gap_cost=1):
'''sumed up version of smit-waterman algorithm in local alignment '''
smatrix = score_matrix(v, u, match_score, gap_cost)
b_, pos = backtrack(smatrix=, u)
return pos, pos + len(b_)
مثال
[ویرایش]- رشته ۱ = ACACACTA
- رشته ۲ = AGCACACA
- w(پرش) = -۱
- w(تطابق) = +۲
برای به دست آوردن بهترین همترازی محلی، از خانه ایی از ماتریس با بیشترین ارزش شروع میکنیم (خانه (i,j)) و به عقب بر میگردیم و به یکی از خانههای (i-1,j), (i,j-1) و (i-1,j-1) میرویم با توجه به مسیری که ماتریس ساخته شدهاست. این رویه را آنقدر تکرار میکنیم که یا به خانه ایی با مقدار صفر برسیم یا در خانه (۰٬۰) باشیم. برای مثال خانه با بیشترین مقدار در جایگاه (۸٬۸) است و با توجه به ماتریس مسیر (۸٬۸), (۷٬۷), (۷٬۶), (۶٬۵), (۵٬۴), (۴٬۳), (۳٬۲), (۲٬۱), (۱٬۱) و (۰٬۰) را به عقب بر میگردیم.
وقتی عمل برگشت تمام شد به این ترتیب همترازسازی را نتیجه میگیریم:
- حرکت روی قطر نشاندهنده یک همترازسازی است (تطابق یا عدم تطابق)
- یک حرکت بالا به پایین نشانده یک حذف است
- یک حرکت چپ به راست نشان دهنده یک درج است.
برای مثال خواهیم داشت:
رشته ۱ = A-CACACTA رشته ۲ = AGCACAC-A
منابع
[ویرایش]- https://dornsife.usc.edu/assets/sites/516/docs/papers/msw_papers/msw-042.pdf
- http://en.wikipedia.org/wiki/Smith–Waterman_algorithm
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC50453
- https://bioinfoguide.com/index.php/algorithms-and-methods/11-smith-waterman-algorithm
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC427531
- https://pubmed.ncbi.nlm.nih.gov/11597340
















