استاندارد رمزنگاری پیشرفته
استاندارد رمزنگاری پیشرفته (به انگلیسی: Advanced Encryption Standard) یا به اختصار AES مشخصهای برای رمزنگاری دادههای دیجیتال است که در سال ۲۰۰۱ توسط مؤسسه ملی فناوری و استانداردهای ایالات متحده ایجاد شد.[۱] این رمز که در ابتدا ریندال (به انگلیسی: Rijndael) نامیده میشد و توسط دو رمزنگار بلژیکی به نامهای ژوآن دیمن (به انگلیسی: Joan Daemen) و وینسنت رینمن (به انگلیسی: Vincent Rijmen) توسعه داده شد.[۲]
استاندارد رمزنگاری پیشرفته توسط دولت ایالات متحده پذیرفته شده و اکنون در سراسر جهان استفاده میشود. این الگوریتم رمزنگاری به جای استاندارد رمزنگاری دادهها (DES) که در سال ۱۹۷۷ منتشر شده،[۳] جایگزین شدهاست. الگوریتم AES یک الگوریتم کلید متقارن است؛ بدین معنی که از یک کلید یکسان برای رمزنگاری و رمزگشایی استفاده میشود.
در ایالات متحده، AES توسط مؤسسه ملی فناوری و استانداردها به عنوان FIPS PUB 197 در نوامبر ۲۰۰۱ اعلان شد.[۱] این اعلان پس از یک فرایند استانداردسازی پنج ساله بود که در این فرایند ۱۵ طرح، تا پیش از معرفی رمز Rijndael به عنوان گزینه مناسب، ارائه و ارزیابی شد. این رمزنگاری به عنوان استاندارد دولت فدرال در ماه مه ۲۰۰۲ پس از تأیید توسط وزارت بازرگانی ایالات متحده آمریکا به کار گرفته شد. AES در استاندارد ISO/IEC 18033-3 قرار گرفتهاست. AES در بستههای رمزنگاری متفاوتی در دسترس بوده و نخستین سایفر باز و در دسترس عموم است که توسط آژانس امنیت ملی ایالات متحده آمریکا (NSA)، پس از بهکارگیری در یک ماژول رمزنگاری تأیید شده NSA، برای اطلاعات خیلی محرمانه تصدیق شدهاست(امنیت AES مطالعه گردد).
نام ریندال (تلفظ هلندی: [ˈrɛindaːl]) ترکیبی از نامهای دو مخترع است. اگر بخواهیم دقیق شویم، استاندارد AES گونهای از ریندال است که اندازه بلاک آن ۱۲۸ بیتی است.
شرح رمز[ویرایش]
استاندارد رمزنگاری پیشرفته بر اساس یک قاعده طراحی به نام substitution-permutation network است و به هر دو صورت سختافزاری و نرمافزاری سریع است.[۴] برخلاف DES، استاندارد رمزنگاری پیشرفته از رمزنگاری فیستل استفاده نمیکند. استاندارد رمزنگاری پیشرفته گونهای از Rijndael است که اندازه بلاک ثابت ۱۲۸ بیتی و اندازه کلید ۱۲۸، ۱۹۲ و ۲۵۶ بیتی دارد. در مقابل، مشخصه per se الگوریتم Rijndael با اندازه کلید و اندازه بلاکی تعیین میشود که میتواند هر ضریبی از ۳۲ بیت، با حداقل ۱۲۸ و حداکثر ۲۵۶ بیت باشد.
استاندارد رمزنگاری پیشرفته روی ماتریسی ۴*۴ از بایتها با ترتیب ستونی، که state نامیده میشود، عمل میکند، اگرچه برخی نسخههای Rijndael اندازه بلاک بزرگتر و ستونهای بیشتری در state دارند. بیشترین محاسبات AES در یک finite field خاص انجام میگیرد.
اندازه کلید استفاده شده در رمز AES، تعداد تکرارهای چرخههای تبدیل (transformation) را تعیین میکند که ورودی، با نام متن عادی (plaintext) را به خروجی نهایی با نام متن رمز شده (ciphertext) تبدیل مینماید. تعداد چرخههای تکرار به صورت زیر است:
- ۱۰ چرخه تکرار برای کلیدهای ۱۲۸ بیتی.
- ۱۲ چرخه تکرار برای کلیدهای ۱۹۲ بیتی.
- ۱۴ چرخه تکرار برای کلیدهای ۲۵۶ بیتی.
هر تکرار شامل چندین مرحله پردازشی است، که یک مرحله بستگی به کلید رمزنگاری دارد. مجموعهای از چرخههای معکوس برای تبدیل متن رمز شده به متن اصلی با استفاده از همان کلید رمزنگاری بکار گرفته میشود.
شرح کلی الگوریتم[ویرایش]
- بسط کلید (KeyExpansion) - کلیدهای چرخه از کلید رمز با استفاده از زمانبندی کلید Rijndael مشتق میشود.
- چرخه اولیه
- AddRoundKey - هر بایت از state با کلید چرخه توسط xor بیت به بیت ترکیب میشود.
- چرخهها
- SubBytes- مرحله جانشین سازی (substitution) غیر خطی که هر بایت با بایت دیگری بر اساس یک جدول جستجو (lookup table) جایگزین میشود.
- ShiftRows- مرحله جابجاسازی (transposition) که هر سطر از state به صورت تکراری در چند مرحله معین شیفت مییابد.
- MixColumns- فرایند در هم ریختن (mixing) ستونها که روی ستونهای state عمل مینماید و چهار بایت از هر ستون را ترکیب مینماید.
- AddRoundKey
- مرحله آخر
- SubBytes
- ShiftRows
- AddRoundKey
مرحله SubBytes[ویرایش]
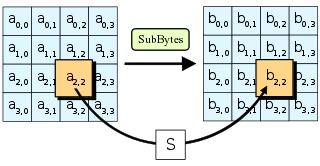
در مرحله SubBytes، هر بایت در ماتریس state با استفاده از substitution box 8 بیتی Rijndael S-box با یک SubByte جایگزین میشود.S-box استفاده شده از معکوس فراینده (multiplicative inverse) روی (GF(۲۸ مشتق شدهاست که به داشتن خصوصیات غیرخطی خوب مشهور است. برای اجتناب از حملات مبتنی بر خصوصیات جبری ساده، S-box به وسیله ترکیب تابع معکوس با یک affine transformation معکوس پذیر ایجاد میشود. affine transformation S-box همچنین به گونهای انتخاب میشود که از هرگونه نقاط ثابت (و همچنین آشفتگی) و هرگونه نقاط ثابت معکوس اجتناب شود.
مرحله ShiftRows[ویرایش]
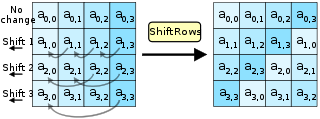
مرحله ShiftRows روی سطرهای state عمل میکند. در این مرحله بایتهای هر سطر به وسیله یک آفست (Offset) معین به صورت چرخشی شیفت مییابد. برای AES، نخستین سطر بدون تغییر باقی میماند. هر بایت از سطر دوم یکی به سمت چپ شیفت مییابد. به صورت مشابه، سطرهای سوم و چهارم به ترتیب با آفستهای دو و سه شیفت مییابند. برای بلاکهای با اندازه ۱۲۸ و ۱۹۲ بیتی، الگوی شیفت دادن یکسان است. سطر n به تعداد n-1 بایت به صورت چرخشی به چپ شیفت مییابد. بدین صورت، هر ستون از state خروجی در این مرحله ترکیب شده بایتهای هر ستون از state ورودی است. (انواع Rijndael با اندازه بلاک بزرگتر، آفستهایی اندکی متفاوت دارند) برای یک بلاک ۲۵۶ بیتی، نخستین سطر بدون تغییر باقی میماند و سطرهای دوم و سوم و چهارم به ترتیب یک، دو و سه بایت شیفت مییابد. این تغییر تنها برای رمز Rijndael با بلاک ۲۵۶ بیتی اعمال میشود چون AES بلاکهای ۲۵۶ بیتی استفاده نمیکند.
مرحله MixColumns[ویرایش]
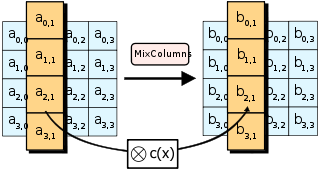
در مرحله MixColumns، چهار بایت از هر ستون state با استفاده از تبدیل خطی معکوس ترکیب میشوند. تابع MixColumns چهار بایت را به عنوان ورودی در نظر میگیرد و چهار بایت را به خروجی میدهد، که هر بایت ورودی بر هر چهار بایت خروجی تأثیر میگذارد. به همراه ShiftRows، مرحله MixColumns آشفتگی و پخش (diffusion) را در رمزنگاری فراهم مینماید.
در طول این عمل، هر ستون توسط ماتریس شناخته شدهای که برای کلید ۱۲۸ بیتی است ضرب میشود.
عمل ضرب بدین صورت تعریف میشود: ضرب در ۱ به معنی بدون تغییر، ضرب در ۲ به معنای جابجایی به سمت چپ و ضرب در ۳ به معنای جابجایی به سمت چپ و سپس انجام XOR را با مقدار اولیه جابهجا نشده. پس از جابجایی، اگر مقدار جابهجا شده بیشتر از ۰xFF باشد، XOR شرطی با ۰x11B باید انجام شود.
به صورت کلی تر، هر ستون به عنوان یک چند جملهای روی (GF(2^8 تلقی میشود و پس از آن پیمانه x4+1 با یک چند جملهای ثابت c(x) = 0x03 · x3 + x2 + x + 0x02 ضرب شده است. ضرایب با معادل مبنای ۱۶ از نمایش دودویی بیتهای چندجملهای [GF(2)[x نمایش داده میشود. مرحله MixColumns همچنین میتواند به صورت ضرب یک ماتریس خاص MDS در یک finite field دیده شود. این فرایند در مقاله ستونهای ترکیبی Rijndael به صورت مفصل تر شرح داده شده است.
مرحله AddRoundKey[ویرایش]
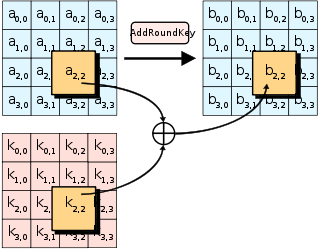
در مرحله AddRoundKey، subkey با state ترکیب میشود. در هر دور، یک subkey از کلید اصلی توسط زمانبند کلید Rijndael مشتق میشود. هر subkey به همان اندازه state است. subkey با ترکیب کردن هر بایت از state با بایت متناظر از subkey با استفاده از XOR بیتی جمع بسته میشود.
بهینهسازی رمز[ویرایش]
در سیستمهای با کلمات ۳۲ بیتی یا بزرگتر، این امکان وجود دارد که به وسیله ترکیب مراحل SubBytes و ShiftRows با مرحله MixColumns با تبدیل آنها به دنبالهای از جستجوهایهای جدول، اجرای این رمزنگاری را سرعت بخشید. این امر نیازمند چهار جدول با ۲۵۶ مدخل ۳۲ بیتی و بهرهگیری از چهار کیلوبایت (۴۰۹۶ کلمه) حافظه (یک کیلوبایت برای هر جدول) است. آنگاه یک چرخه میتواند با ۱۶ جستجوی جدول و ۱۲ عمل OR انحصاری ۳۲ بیتی و در ادامه با چهار عمل OR انحصاری ۳۲ بیتی در مرحله AddRoundKey انجام میشود.[۵]
اگر اندازه جدول چهار کیلوبایتی برای پلت فرم مقصد بزرگ است، جستجوی جدول میتواند با یک جدول با ۲۵۶ مدخل ۳۲ بیتی (یعنی ۱ کیلوبایت) با استفاده از تکرارهای چرخشی انجام گردد.
با استفاده از رویکرد بایت گرا، ترکیب مراحل SubBytes، ShiftRows و MixColumns به یک چرخه تنها امکانپذیر است.[۶]
امنیت[ویرایش]
تا ماه مه ۲۰۰۹، تنها حملات منتشر شده موفق علیه AES کامل، حملات Side-Channel در برخی از پیادهسازیهای خاص بود. آژانس امنیت ملی امریکا (NSA) همه AESهای فینالیست، از جمله Rijndael را بازبینی کرد، و اظهار داشت که همه آنها برای اطلاعات غیر طبقهبندی شده دولت ایالات متحده به اندازه کافی امن است. در ماه ژوئن سال ۲۰۰۳، دولت ایالات متحده اعلام کرد که AES میتواند برای محافظت از اطلاعات طبقهبندی شده مورد استفاده قرار گیرد:
طراحی و قدرت تمام طول کلیدهای الگوریتم AES (به عنوان مثال ۱۲۸، ۱۹۲ و ۲۵۶) برای محافظت از اطلاعات طبقهبندی شده تا سطح محرمانه کافی است. اطلاعات خیلی محرمانه نیاز به استفاده کلیدهای با طول ۱۹۲ یا ۲۵۶ دارد. پیادهسازی AES در محصولات در نظر گرفته شده برای حفاظت از سیستمهای امنیت ملی و / یا اطلاعات باید توسط NSA، پیش از استفاده، بازبینی و مجوز داده شود.[۷]
AES دارای ۱۰ چرخه برای کلیدهای ۱۲۸ بیتی، ۱۲ چرخه برای کلیدهای ۱۹۲ بیتی و ۱۴ چرخه برای کلیدهای ۲۵۶ بیتی میباشد. در سال ۲۰۰۶، بهترین حملات شناخته شده در ۷ چرخه برای کلیدهای ۱۲۸ بیتی، ۸ چرخه برای کلیدهای ۱۹۲ بیتی، و ۹ چرخه برای کلیدهای ۲۵۶ بیتی بودند.[۸]
حملات شناخته شده[ویرایش]
برای رمزنگاران، شکست (break) رمزنگاری هر چیزی است که سریع تر از انجام brute force (رمزگشایی آزمایشی برای هر یک کلید) باشد. حملات brute force با تکنولوژی فعلی نشدنی هستند. بزرگترین حمله موفقیت آمیز و به صورت عمومی شناخته شده brute force، در برابر هر گونه رمزنگاری block-cipher در برابر RC5 با کلید ۶۴ بیتی به وسیله distributed.net در سال ۲۰۰۶ بود.[۹]
AES است شرح جبری نسبتاً ساده دارد.[۱۰] در سال ۲۰۰۲، یک حمله نظری، با عنوان "حمله XSL"، توسط Nicolas Courtois و Josef Pieprzyk اعلام شد، که به نظر میرسید ضعفی را در الگوریتم AES به علت شرح ساده نشان میدهد.[۱۱] از آن زمان به بعد، مقالات دیگر نشان دادهاند که که حمله ارائه شده ناکارآمد است. حمله ایکساسال مطالعه شود.
در طول روند AES، توسعه دهندگان الگوریتمهای محاسباتی درباره Rijndael نوشتند، "... ما نگران استفاده از آن... در برنامههای کاربردی حساس امنیتی هستیم."[۱۲] با این حال، در ماه اکتبر سال ۲۰۰۰ و در پایان فرایند انتخاب AES، Bruce Schneier، توسعه دهنده الگوریتم محاسباتی Twofish، در حالی که فکر میکرد حملات موفق دانشگاهی روی Rijndael روزی توسعه داده خواهد شد، نوشت: "من باور ندارم که هیچکسی حملهای را کشف کند که اجازه دهد کسی ترافیک Rijndael را بخواند."[۱۳]
در تاریخ ۱ ژوئیه ۲۰۰۹، Bruce Schneier، در وبلاگش[۱۴] در مورد یک حمله مرتبط با کلید در نسخههای ۱۹۲-بیتی و ۲۵۶ بیتی AES خبر داد، که توسط Alex Biryukov و Dmitry Khovratovich کشف شده بود[۱۵] که این حمله از زمانبندی کلید تا حدودی ساده AES استفاده کرده ودارای پیچیدگی ۲119 است. در دسامبر ۲۰۰۹، این پیچیدگی به ۲99.5 بهبود یافته بود. این حمله دنباله حملهای بودکه پیش از آن در سال ۲۰۰۹ توسط Alex Biryukov، Dmitry Khovratovich و Nikolić Ivica با یک پیچیدگی از ۲96 برای یکی از هر ۲35 کلید بود.[۱۶]
در تاریخ ۳۰ ژوئیه ۲۰۰۹ حمله دیگری در وبلاگ Bruce Schneier گزارش شد[۱۷] و به عنوان یک نسخه پیش از چاپ در تاریخ ۳ اوت ۲۰۰۹ منتشر شد.[۱۸] این حمله جدید، توسط Alex Biryukov، Orr Dunkelman، Nathan Keller، Dmitry Khovratovich و Adi Shamir، روی AES-256 است که با استفاده از تنها دو کلید مربوط و زمان ۲39 برای بازیابی کلید ۲۵۶ بیتی در نسخههای ۹ چرخهای، یا زمان ۲45 برای یک نسخه ۱۰ چرخهای با نوعی قوی تر از حمله مرتبط با subkey، یا زمان ۲70 برای نسخه ۱۱ چرخهای انجام میشود. AES 256 بیتی از ۱۴ چرخه استفاده مینماید، بنابراین چنین حملاتی روی AES کامل مؤثر نیست.
در نوامبر ۲۰۰۹، اولین حمله تشخیص کلید روی نسخهای از AES-128 کاهش یافته به ۸ چرخه، به عنوان یک نسخه پیش از چاپ منتشر شد.[۱۹] این حمله تشخیص کلید، نسخهای بهبود یافته از حملات rebound یا start-from-the-middle برای جایگشتها (permutations) مشابه AES است، که دو چرخه متوالی از جایگشت را به عنوان کاربردی از سوپر Sbox در نظر میگیرد. این حمله روی نسخه ۸ چرخهای AES-128 با پیچیدگی زمانی ۲48 و یک پیچیدگی حافظه ۲32 عمل میکند.
در ژوئیه ۲۰۱۰ Vincent Rijmen مقاله طعنه آمیزی برای حملات "chosen-key-relations-in-the-middle" روی AES-128 منتشر کرد.[۲۰]
اولین حمله بازیابی کلید روی AES کامل توسط Andrey Bogdanov، Dmitry Khovratovich و Christian Rechberger بود و در سال ۲۰۱۱ منتشر شد.[۲۱] حمله بر اساس bicliques بوده و با ضریب ۴ سریعتر از brute force است. برای AES-192 و AES-256، به ترتیب به ۲189.7 و ۲254.4 عمل نیازمند است.
حملات غیر مستقیم[ویرایش]
حملات غیرمستقیم (به انگلیسی: Side-Channel attacks) به رمز مورد نظر حمله نمیکنند اما به پیادهسازی رمز بر روی سیستمهایی که سهواً اطلاعات را فاش مینمایند، حمله میکنند. چندین حملات شناخته شده روی پیادهسازیهای خاصی از AES وجود دارد.
در آوریل سال ۲۰۰۵، D.J. Bernstein یک حمله cache-timing را اعلام کرد که او این حمله را برای شکستن یک سرور سفارشی که از رمزگذاری AES کتابخانه OpenSSL استفاده مینمود، بکار گرفت.[۲۲] این حمله نیاز به بیش از ۲۰۰ میلیون پیام رمز نشده داشت.[۲۳] سرور سفارشی به گونهای طراحی شده بود که تا حد ممکن اطلاعات زمانی را انتشار میداد (سرور گزارشی از تعداد چرخههای انجام گرفته توسط عملیات رمزگذاری را باز میگرداند)؛ با این حال، همانگونه که Bernstein نشان داد، "کاهش دقت مهرهای زمانی (timestamp) سرور، یا حذف آنها را از پاسخ سرور، این حمله را متوقف نمینماید: مشتری به سادگی با استفاده از زمان رفت و برگشت بر اساس ساعت محلی خودش، استفاده نموده و اختلالات افزایش یافته را به وسیله میانگین گیری روی تعداد زیادی از نمونهها جبران مینماید. "[۲۲]
در اکتبر سال ۲۰۰۵، Dag Arne Osvik، Adi Shamir و Tromer Eran مقالهای را ارائه دادند که چندین حمله cache-timing را روی AES نشان میداد.[۲۴] یک حمله قادر به دست آوردن تمام کلید AES پس از ۸۰۰ عمل آغازسازی رمزگذاری، در مجموع ۶۵ میلی ثانیه، بود. این حمله نیازمند آن است که مهاجم قادر به اجرای برنامههایی بر روی همان سیستم یا همان پلت فرمی که AES در حال انجام است، باشد.
در دسامبر ۲۰۰۹، حملهای روی برخی از پیادهسازیهای سختافزاری منتشر شد که از تجزیه و تحلیل خطای تفاضلی (differential fault analysis) استفاده میکند و اجازه میدهد کلیدی با پیچیدگی از ۲32 را بازیابی نمود.[۲۵]
در نوامبر ۲۰۱۰ Endre Bangerter، David Gullasch و Stephan Krenn مقالهای را چاپ نمودند که روشی عملی برای بازیابی نزدیک به بی درنگ کلیدهای رمز AES-128 بدون نیاز به متن رمزنگاری یا متنی را توضیح میداد. این روش همچنین روی پیادهسازیهای AES-128 که جداول فشرده سازی را استفاده مینماید، مانند OpenSSL، عمل میکند.[۲۶] همانند برخی از حملات قبلی، این حمله نیازمند این قابلیت است که بتواند روی سیستمی که رمزگذاری AES را انجام میدهد، اجرا شود، که اینکار میتواند توسط آلودگی به تروجان انجام گیرد.[۲۷]
جستارهای وابسته[ویرایش]
منابع[ویرایش]
- ↑ ۱٫۰ ۱٫۱ "Announcing the ADVANCED ENCRYPTION STANDARD (AES)" (PDF). Federal Information Processing Standards Publication 197. United States National Institute of Standards and Technology (NIST). November 26, 2001. Retrieved October 2, 2012.
- ↑ John Schwartz (October 3, 2000). "U.S. Selects a New Encryption Technique". New York Times.
- ↑ Westlund, Harold B. (2002). "NIST reports measurable success of Advanced Encryption Standard". Journal of Research of the National Institute of Standards and Technology.
- ↑ Bruce Schneier, John Kelsey, Doug Whiting, David Wagner, Chris Hall, Niels Ferguson, Tadayoshi Kohno, Mike Stay (May 2000). "The Twofish Team's Final Comments on AES Selection" (PDF). Archived from the original (PDF) on 2 January 2010. Retrieved 16 November 2012.
{{cite web}}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - ↑ "Efficient software implementation of AES on 32-bit platforms".[پیوند مرده] Lecture Notes in Computer Science: 2523. 2003
- ↑ http://code.google.com/p/byte-oriented-aes
- ↑ Lynn Hathaway (June 2003). "National Policy on the Use of the Advanced Encryption Standard (AES) to Protect National Security Systems and National Security Information" (PDF). Retrieved 2011-02-15.
- ↑ John Kelsey, Stefan Lucks, Bruce Schneier, Mike Stay, David A. Wagner, and Doug Whiting, Improved Cryptanalysis of Rijndael, Fast Software Encryption, 2000 pp213–230 [۱]
- ↑ Ou, George (April 30, 2006). "Is encryption really crackable?". Ziff-Davis. Archived from the original on 7 August 2010. Retrieved August 7, 2010.
- ↑ "Sean Murphy". University of London. Retrieved 2008-11-02.
- ↑ Bruce Schneier. "AES News, Crypto-Gram Newsletter, September 15, 2002". Archived from the original on 7 July 2007. Retrieved 2007-07-27.
- ↑ Niels Ferguson, Richard Schroeppel, Doug Whiting (2001). "A simple algebraic representation of Rijndael". Proceedings of Selected Areas in Cryptography, 2001, Lecture Notes in Computer Science. اشپرینگر ساینس+بیزینس مدیا. pp. 103–111. Archived from the original (PDF/پستاسکریپت) on 4 November 2006. Retrieved 2006-10-06.
{{cite conference}}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - ↑ Bruce Schneier, AES Announced, October 15, 2000
- ↑ Bruce Schneier (2009-07-01). "New Attack on AES". Schneier on Security, A blog covering security and security technology. Archived from the original on 8 February 2010. Retrieved 2010-03-11.
- ↑ Biryukov, Alex (2009-12-04). "Related-key Cryptanalysis of the Full AES-192 and AES-256". Retrieved 2010-03-11.
{{cite web}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Nikolić, Ivica (2009). "Distinguisher and Related-Key Attack on the Full AES-256". Advances in Cryptology - CRYPTO 2009. Springer Berlin / Heidelberg. pp. 231–249. doi:10.1007/978-3-642-03356-8_14. ISBN 978-3-642-03355-1.
{{cite book}}:|access-date=requires|url=(help) - ↑ Bruce Schneier (2009-07-30). "Another New AES Attack". Schneier on Security, A blog covering security and security technology. Retrieved 2010-03-11.
- ↑ Alex Biryukov (2009-08-19). "Key Recovery Attacks of Practical Complexity on AES Variants With Up To 10 Rounds". Archived from the original on 28 January 2010. Retrieved 2010-03-11.
{{cite web}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Henri Gilbert (2009-11-09). "Super-Sbox Cryptanalysis: Improved Attacks for AES-like permutations". Retrieved 2010-03-11.
{{cite web}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Vincent Rijmen (2010). "Practical-Titled Attack on AES-128 Using Chosen-Text Relations" (PDF).
- ↑ Andrey Bogdanov, Dmitry Khovratovich, and Christian Rechberger (2011). "Biclique Cryptanalysis of the Full AES" (PDF). Archived from the original (PDF) on 6 March 2016. Retrieved 6 December 2012.
{{cite web}}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - ↑ ۲۲٫۰ ۲۲٫۱ "Index of formal scientific papers". Cr.yp.to. Retrieved 2008-11-02.
- ↑ Bruce Schneier. "AES Timing Attack". Archived from the original on 12 February 2007. Retrieved 2007-03-17.
- ↑ Dag Arne Osvik1 (2005-11-20). "Cache Attacks and Countermeasures: the Case of AES" (PDF). Retrieved 2008-11-02.
{{cite journal}}: Cite journal requires|journal=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ Dhiman Saha, Debdeep Mukhopadhyay, Dipanwita RoyChowdhury. "A Diagonal Fault Attack on the Advanced Encryption Standard" (PDF). Archived from the original (PDF) on 22 December 2009. Retrieved 2009-12-08.
{{cite journal}}: Cite journal requires|journal=(help)نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - ↑ Endre Bangerter, David Gullasch and Stephan Krenn (2010). "Cache Games – Bringing Access-Based Cache Attacks on AES to Practice" (PDF).
- ↑ http://news.ycombinator.com/item?id=1937902
- Nicolas Courtois, Josef Pieprzyk, "Cryptanalysis of Block Ciphers with Overdefined Systems of Equations". pp267–287, ASIACRYPT 2002.
- Joan Daemen, Vincent Rijmen, "The Design of Rijndael: AES - The Advanced Encryption Standard." Springer, 2002. ISBN 3-540-42580-2.
- Christof Paar, Jan Pelzl, "The Advanced Encryption Standard", Chapter 4 of "Understanding Cryptography, A Textbook for Students and Practitioners". (companion web site contains online lectures on AES), Springer, 2009.

