گراف چندگانه

شکل (۱)
گراف چندگانه

در نظریه گراف گراف چندگانه یا شبه گراف به گرافی گفته می‌شود که مجاز است یالهای چندگانه داشته باشد که به آنها یالهای موازی هم گفته می‌شود.

بنابراین دو راس ممکن است با بیش از یک یال بهم متصل شوند. گراف چندگانه را می‌توان بازوج مرتب(G=(V, E معرفی کرد که در آن

• V مجموعهٔ گره‌ها یا رأس‌های گراف است.
• E مجموعهٔ چندگانه‌ای از زوج نامرتب یال‌ها که لبه‌ها یا خط نامیده می‌شوند.

یال‌های چندگانه

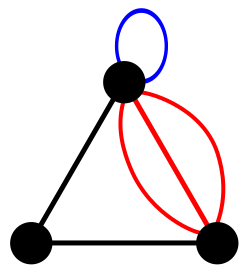
یال‌های چندگانه یال‌هایی هستند که بین دو راس معین و مشترک قرار می‌گیرند. یال‌های چندگانه با درجهٔ d_ij بین راسهای i و j برابرند بایک عدد صحیح d_ij که 1 <d_ij به عنوان درایه ی (i,j)ماتریس مجاورت گراف چندگانه نوشته می‌شود. درایهٔ 0<d_kk که مربوط به قطر ماتریس مجاورت گراف است بیانگر وجود حلقه روی آن راس است. شکل ۲ بیانگر مثالی از گراف چندگانه وماتریس مجاورت آن است. توجه داریم که این گراف همچنان متقارن است. اما ممکن است درایه‌های غیر از قطر اصلی آن هر عددی بزرگترمساوی از ۰ باشد و درایه‌های قطر اصلی آن ۱ نیز باشد.

شکل (۲)
ماتریس مجاورت گراف چندگانه

تفاوت شبه گراف و گراف چندگانه

برخی ریاضی‌دانان، گراف چندگانه را متمایز از شبه‌گراف تعریف می‌کنند. براساس این تعریف، گراف چندگانه فاقد طوقه است (طوقه یا حلقه، یالی است که یک راس را به خودش متصل می‌کند. به عبارت دیگر راس ابتدایی و انتهایی آن یکسان است). شبه‌گراف اما می‌تواند علاوه‌ بر یال چندگانه، طوقه نیز داشته باشد. بر مبنای این تعریف، شبه‌گراف، گرافی چندگانهٔ اما مجاز به داشتن طوقه است.

شکل (۳)
شبه گراف

شکل (۴)
گراف چندگانه

مثالی از کاربرد گراف چندگانه

گراف چندگانه را می‌توان در مدلسازی پروازهای ارائه شده توسط یک شرکت هوائی استفاده کرد؛ که گراف چندگانه می‌تواند مثل گراف ساده با جفتهای یالهای موازی مستقیم واسط شهرها باشد که پروازهای به/از یک مکان را مدلسازی کند. کاربرد دیگر گرافهای چندگانه در مدلسازی شبکه‌است.

نحوهٔ ساختن گراف چندگانه

G با مجموعه رئوس{V = {v1, v2, v3,... , vn و مجموعهٔ یالهای{E = {e1, e2, e3,... , en

• گراف را شیئی در نظر می‌گیریم که شامل لیست رئوس است.
• هر راس شیئی است که لیستی ازیالهارا دارد که بیانگر یالهای خروجی از آن راسند.
• هر یال شیئی است که شامل اشاره گر به راسی است که به آن ختم شده.

در این روش هر راس به یال (های) خود به چشم یال خروجی نگاه می‌کند و فقط خود یال می‌داند که به کجا ختم خواهد شد.

• الگوریتم بالا برای گرافهای چندگانه به راحتی توسط داده ساختاری مثل لیست پیوندی قابل پیاده‌سازی است.
• هر شی –چه یال و چه راس –دقیقاً یک نماینده دارد. یعنی مربوط به فقط یک راس یا یال است. در نتیجه تمام تغییراتی مثل حذف یا اضافه به صورت محلی انجام می‌شود. (فقط یکی از لیست‌ها تغییر می‌کند)

منابع

• ویکی‌پدیای انگلیسی، گراف چندگانه
• دانشنامه رشد
• -- from Wolfram MathWorld