لم تزریق برای زبان‌های منظم

در نظریهٔ زبان‌های صوری، لم تزریق برای زبان‌های منظم یک ویژگی ضروری برای همهٔ زبان‌های منظم را توصیف می‌کند. به‌طور غیر صوری، بیان می‌کند که هر کلمهٔ به اندازهٔ کافی بزرگ در یک زبان منظم می‌تواند تزریق شود — یعنی یک قسمت میانی کلمه به تعداد دل‌خواه تکرار شود — تا کلمهٔ جدیدی ایجاد شود که همچنین در همان زبان قرار گیرد.

مخصوصا لم تزریق بیان می‌کند که برای هر زبان منظم L یک عدد ثابت p وجود دارد به‌طوری‌که هر کلمه w در L با طول حداقل p می‌تواند به سه زیر رشته تقسیم شود، w = xyz، که در آن بخش میانی y خالی نیست، طوری‌که کلمه‌های xz، xyz، xyyz، xyyyz، ... ساخته شده با به تعداد دل‌خواه بار تکرار y (شامل صفر بار) باز هم در L باشند. این فرایند تکرار به «تزریق» معروف است. علاوه بر این، لم تزریق تضمین می‌کند که طول xy حداکثر p خواهد بود، که این محدودیتی بر راه‌هایی که w می‌تواند تقسیم شود تحمیل می‌کند. زبان‌های متناهی به وضوح لم تزریق را با قرار دادن p برابر طول بیشترین رشته در L به اضافهٔ یک ارضا می‌کنند.

لم تزریق اولین بار توسط دانا اسکات و مایکل رابین در ۱۹۵۹ اثبات شد. این لم برای رد کردن خاصیت منظم بودن یک زبان خاص مورد سؤال کاربرد دارد. این لم یکی از معدود لم‌های تزریق است، که هر کدام قصد مشابهی دارند.

شرح صوری

فرض می‌کنیم L یک زبان منظم باشد. در این صورت عدد صحیح p ≥ 1 تنها وابسته به L وجود دارد طوری‌که هر رشتهٔ w در L با طول حداقل p (به p طول تزریق گفته می‌شود) می‌تواند به صورت w = xyz نوشته شود (w می‌تواند به سه زیررشته تقسیم شود)، طوری‌که شرط‌های زیر را ارضا کند:

1. |y| ≥ 1;
2. |xy| ≤ p
3. for all i ≥ 0, xyⁱz ∈ L

y زیر رشته‌ای است که می‌تواند تزریق شود (حذف شود یا به به هر تعداد بار تکرار شود، و رشتهٔ حاصل در هر حال در L باشد). (۱) به این معنی است که طول لوپ y که تزریق می‌شود باید حداقل یک باشد. (۲) به این معنی است که لوپ y باید در p کاراکتر اول واقع باشد. |x| باید کوچکتر از p باشد (نتیجهٔ (۱) و (۲))، غیر از این دیگر هیچ محدودیتی بر روی x و z وجود ندارد.

به زبان ساده، برای هر زبان منظم L، هر کلمهٔ به اندازهٔ کافی بزرگ (در L) می‌تواند به ۳ قسمت تقسیم شود. مثلاً w = xyz، طوری‌که همهٔ رشته‌های xy^kz برای هر k≥0 هم در L باشند.

در زیر یک صورت‌بندی صوری لم تزریق آمده‌است:

${\begin{array}{l}(\forall L\subseteq \Sigma ^{*})\\\quad ({\mbox{regular}}(L)\Rightarrow \\\quad ((\exists p\geq 1)((\forall w\in L)((|w|\geq p)\Rightarrow \\\quad \quad ((\exists x,y,z\in \Sigma ^{*})(w=xyz\land (|y|\geq 1\land |xy|\leq p\land (\forall i\geq 0)(xy^{i}z\in L))))))))\end{array}}$

کاربرد لم

لم تزریق معمولاً برای اثبات نامنظم بودن یک زبان خاص مورد استفاده قرار می‌گیرد. یک اثبات به وسیلهٔ برهان خلف می‌تواند شامل یک کلمه (با طول خواسته شده) در زبان باشد که فاقد خاصیت بیان شده در لم تزریق است.

به‌طور مثال زبان {L = {aⁿbⁿ : ≥ 0 روی الفبای {Σ = {a, b می‌تواند به روشی که در ادامه می‌آید اثبات شود که نامنظم است. فرض کنید w، x، y، z، p و i همان متغیرهایی باشند که در صورت لم تزریق در بالا استفاده شدند. فرض کنید w در L به صورت w = a^pb^p داده شده باشد. با استفاده از لم تزریق، باید یک تجزیه w = xyz با xy| ≤ p| و y| ≥ 1| وجود داشته باشد طوری‌که xyⁱz به ازای هر i در L باشد. با استفاده از xy| ≤ p| می‌دانیم که y فقط شامل نمونه‌های a است. علاوه بر این، چون y| ≥ 1|، شامل حداقل یک نمونه از a است. حال y را تزریق می‌کنیم: xy²z دارای نمونه‌های بیشتری از حرف a نسبت به حرف b است، زیرا ما تعدادی نمونهٔ a بدون اضافه کردن نمونه‌ای از b اضافه کردیم. بنابراین xy²z در L نیست. پس به تناقض رسیدیم. از این رو، این فرض که L منظم است باید نادرست باشد. پس L منظم نیست.

اثبات لم تزریق

برای هر زبان منظم یک ماشین حالات متناهی (FSA) وجود دارد که آن زبان را می‌پذیرد. تعداد حالات در چنین ماشین حالات متناهی‌ای شمرده می‌شود و این تعداد به عنوان طول تزریق p استفاده می‌شود. برای یک رشته به طول حداقل p، فرض کنید s₀ حالت آغازین و s₁, ..., s_p ترتیب p حالت بعدی باشد که در فرایند تولید رشته طی می‌شوند. از آن‌جا که FSA تنها p حالت دارد، در این دنباله که در آن p+1 حالت طی شده‌است باید حداقل یک حالت وجود داشته باشد که تکرار شده‌است. نام این حالت را S می‌گذاریم. انتقالاتی که ماشین را از اولین مواجهه با S به دومین مواجهه با S می‌برند با یک رشته تطابق دارند. این رشته در لم y نامیده می‌شود، و از آن‌جایی که ماشین بدون بخش y به یک رشته می‌رسد، یا رشتهٔ y می‌تواند به تعداد دل‌خواه بار تکرار شود، شرط‌های لم ارضا می‌شوند.

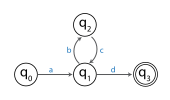
به‌طور مثال شکل زیر یک FSA را نشان می‌دهد:

FSA رشتهٔ abcd را می‌پذیرد. از آن‌جا که این رشته طولی دارد که حداقل به اندازهٔ تعداد حالات است، اصل لانه کبوتری نشان می‌دهد که باید حداقل یک حالت تکراری بین حالت آغازین و ۴ حالت بعدی وجود داشته باشد. در این مثال فقط q₁ حالت تکراری است. از آن‌جا که زیر رشتهٔ bc ماشین را درون انتقالاتی که در حالت q₁ شروع می‌شوند و در حالت q₁ تمام می‌شوند می‌برد، این قسمت می‌تواند با دادن رشتهٔ abcbcd تکرار شود و FSA هنوز می‌پذیرد. متناوباً، قسمت bc می‌تواند حذف شود و FSA کماکان دادن رشتهٔ ad را می‌پذیرد. در عبارات لم تزریق، رشتهٔ abcd شکسته شده به یک قسمت x که a است، یک قسمت y که bc است و یک قسمت z که d است.

نسخهٔ کلی لم تزریق برای زبان‌های منظم

اگر یک زبان L منظم باشد، یک عدد p ≥ 0 (طول تزریق) وجود دارد به‌طوری‌که هر رشتهٔ uwv در L با w| ≥ p| می‌تواند به فرم

uwv = uxyzv

نوشته شودبا رشته‌های y ،x و z طوری‌که xy| ≤ p ، |y| ≥ 0| و

uxyⁱz به ازای هر i در L باشد.

این نسخه از لم می‌تواند در اثبات نامنظم بودن زبان‌های بیشتری مورد استفاده قرار بگیرد، زیرا شرایط سختگیرانه‌تری را روی زبان تحمیل می‌کند.

عکس لم صحیح نیست

در نظر داشته باشید با این که لم تزریق بیان می‌کند که هر زبان منظم شرایط بالا را ارضا می‌کنند، عکس این گزاره صحیح نیست: یک زبان که این شرایط را ارضا می‌کند ممکن است نامنظم باشد. به بیان دیگر، هر دو نسخهٔ اصلی و کلی لم تزریق یک شرط لازم و نه کافی را برای منظم بودن زبان ارائه می‌کنند.

به‌طور مثال زبان L زیر را در نظر بگیرید:

${\begin{aligned}L&=\{uvwxy:u,y\in \{0,1,2,3\}^{*};v,w,x\in \{0,1,2,3\}\land (v=w\lor v=x\lor x=w)\}\\&\cup \{w:w\in \{0,1,2,3\}^{*}\land {\text{precisely 1/7 of the characters in }}w{\text{ are 3's}}\}\end{aligned}}$.

به بیان دیگر، L شامل همهٔ رشته‌ها روی الفبای {0,1،2,3} با یک زیر رشتهٔ به طول 3 شامل یک حرف تکراری است، و همچنین رشته‌هایی که دقیقاً 1/7 کاراکترهای آن رشته 3 باشند. این زبان منظم نیست ولی با این حال هنوز می‌تواند با p = 5 «تزریق» شود. یک رشتهٔ s با طول حداقل 5 را در نظر بگیرید. سپس از آن‌جا که الفبا فقط 4 حرف دارد، حداقل دو تا از پنج حرف رشته باید تکراری باشند. آن‌ها با حداکثر سه حرف از هم جدا شده‌اند.

• اگر حرف‌های تکراری با 0 یا 1 حرف جدا شده باشند، یکی از دو حرف دیگر را که تأثیری روی زیررشته‌ای که شامل حروف تکراری است نداشته باشد تزریق می‌کنیم.
• اگر حروف تکراری با 2 یا 3 حرف جدا شده باشند، دو تا از حروفی که آن‌ها را از هم جدا می‌کند تزریق می‌کنیم. تزریق کردن بالا یا پایین یک زیررشته به طول 3 می‌سازد که که شامل دو حرف تکراری است.
• دومین شرط L تضمین می‌کند که L منظم نیست: به عنوان مثال، بی‌نهایت رشته در L وجود دارند که نمی‌توان با تزریق کردن یک رشتهٔ کوچک‌تر آن‌ها را به دست آورد.

برای یک آزمایش عملی که دقیقاً زبان‌های منظم را مشخص می‌کند، نظریهٔ مایهیل-نروده را مشاهده کند. روش بارز برای اثبات منظم بودن یک زبان ساختن یک ماشین حالات متناهییا یک عبارت منظمبرای آن زبان است.

منابع

Wikipedia contributors, "Pumping lemma for regular languages," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Pumping_lemma_for_regular_languages&oldid=607161557 (accessed May 21, 2014).