پسپرش (الگوریتم)
در الگوریتمهای پسگرد (backtrack) روشی به نام پَسپَرش (backjumping) وجود دارد که باعث کاهش فضای جستجو، در نتیجه افزایش بهرهوری است. در پسگرد همواره یک سطح در درخت جستجو بالا میرویم زمانیکه تمامی مقادیر گرهها بررسی شده باشند، اما در روش پسپرش ممکن است چندین سطح به بالا پرش انجام دهیم. در این مقاله، مقادیر امتحانی ثابتی در نظر گرفتهایم x1 , x2 , … ,xn که ممکن است به صورت غیر مرتّب نیز از آنها استفاده نماییم.
-
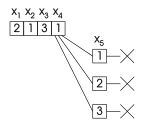
درخت جستجو توسط پسگرد
-
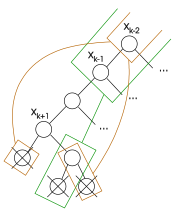
یک پسپرش: گره خاکستری بازدید نمیشود
تعریف[ویرایش]
در روش پسگرد زمانیکه مقادیر یک متغیّر مورد بررسی قرار بگیرد و جستجو بینتیجه پایان یابد، الگوریتم مقدار آخرین متغیرهای گره پیشین مورد بررسی قرار میدهد ولی اگر به انتها رسید و تمامی گرهها بررسی شد و به جواب درستی نرسیدیم، مقدار گره جستجو را تغییر و عملیات جستجو دوباره تکرار میشود. اگر شرایط به این گونه باشد x1=a1,…،xk =ak و تمامی مقادیر برای xk+1 بدون نتیجه برای پیدا کردن راه کار به پایان برسد الگوریتم یک سطح به بالا یعنی گره xk میرود؛ و در صورت امکان، مقدار را عوض کرده و به بالا بازمیگردد و سپس دوباره این مراحل را تکرار میکند.
انتخاب مقدار تخصیص جزئی xk+1 همواره به صورت کامل برای پیدا کردن راه حل ضروری نیست چرا که اجباراً ما را به سمت جواب پایانی هدایت نمیکند. اگر شرایط به این گونه باشد x1=a1,…xk=ak و تمامی مقادیر برای xk+1 بدون نتیجه برای پیدا کردن راه کار به پایان برسد الگوریتم یک سطح به بالا یعنی گره xk رفته و در صورت امکان مقدار را عوض کرده سپس دوباره این مراحل را تکرار میکند. انتخاب مقدار تخصیص جزئی xk+1 همواره به صورت کامل برای پیدا کردن راه حل ضروری نیست اما یک پیشوند تخصیص جزئی ممکن است در حل مسائل ارزش زیادی داشته باشد. برای این منظور از ایندکسهایی با شرط j <k استفاده میکنیم همانند x1,…،xj=a1,…،aj. این کار زمانی اتفاق میافتد که قابل بسط بیشتر برای ساختن یک راه حل برای xk+1 نیستیم. اگر الگوریتم بتواند اثبات کند این نکته را، میتواند به صورت مستقیم یک گره جدیدی برای xj به جای xk جدید انتخاب نماید.
میزان بهرهوری الگوریتم پسپرش میزان پرش به عقبی است که میتواند اتفاق بیفتد به صورت ایدهآل در این روش میتوان از xk+1 پرش کرد به هر متغیری مانند xj که در سری وجود دارد رفت یا در بدترین حالت پیش آمده عمل پرش به xk+1 انجام پذیرد؛ که به این خانه، خانه پرش امن گفته میشود.
تشخیص این نکته که آیا پرش امن است یا خیر همواره امکانپذیر نیست، پیدا کردن روشهایی برای اطمینان یافتن پرشهای امن کاری است که در این الگوریتم سهی میشود انجام داد. عملاً در الگوریتم پسپرش از حداقل ایندکس گذاریها برای پیدا کردن خانه امن استفاده میشود تا بهرهوری کل الگوریتم حفظ شود. الگوریتمهای مختلف روشهای متنوعی را برای یافتن پرش امن مورد استفاده قرار میدهند؛ که البته هزینههای هر کدام از این روشها نیز متفاوت است. اما ممکن است هزینههای تحمیلی ارزش این را داشته باشد که کاهش جستجوی بخشهایی از درخت حذف نماید.
پسپرش در گرههای برگ[ویرایش]
در پسپرش سادهترین شرایط زمانی است که بدون اینکه شاخهٔ دیگری مورد بررسی قرار بگیرد ثابت شود تمامی مقادیری که یک گره با موارد مورد جستجو نامرتب هستند. قید رضایت بخش این است که قدم بعدی بسیار با اطمینان و محکم برداشته شود که موجب خراب شدن روند جستجو با توجه به تمامی متغیّرهای درگیر نشود در غیر این صورت این گام نامناسب نامیده میشود. این موضوع بیانگر این نکتهاست که پیدا کردن قدم کاملاً مناسب بعضی وقتها وابسته به گرههایی است که تا به حال درگیر نشدهاند و برخی متغیرهای تخصیص داده نشده ممکن نیست مورد بررسی قرار بگیرند مادامیکه شرایط دیگری به وجود نیاید.
به شرایطی که در آن همه مقادیر داده شده متغیر xk+1 دارای مقادیر نامناسب در سری x1,…،xk = a1,…،ak باشد را گره بنبست مینامیم. این شرایط دقیقاً زمانی میتواند رخ دهد که متغیر xk+1 یک برگ از درخت جستجو باشد. (دقیقاً همانند گرههایی که تنها برگهایی به عنوان فرزند دارند و در شکل این مقاله میتوانید آن را ببینید)
الگوریتم پسپرش ارائه شده توسط Gasching تنها عملیات پرش به عقب را در برگهای انتهایی درخت انجام میدهد در این روش مقادیر احتمالی برای xk+1 امتحان شده در گره آخر، در صورت نامناسب بودن نتیجه مقایسه عملیات فرایند برگشت به عقب را فراخوانی میکند. در واقع این روش کمی با عملیات پرش به عقب معمول متفاوت است.
پرش امن به سادگی با محاسبهٔ سادهای برای هر مقدار ak+1 بدست میآید، کمترین پیشوند موجود در سری x1,…،xk = a1,…،ak بدست میآید. به عنوان مثال اگر برای ak+1 مقدار xk+1 محتمل باشد، الگوریتم ما حالتهای مناسب و محتمل زیر را بررسی و در مورد مناسب بودن خانه نتیجهگیری میکند:
| ... | ||||
| ... | ||||
| ... | ||||
پرش امن برای خانههایی که نامناسب شناخته میشوند کوچکترین ایندکس گرهاست مثلاً پرش امن در شرایط xk+1=ak+1 تنها مقدار محتمل مناسب برای xk+1 است. از آنجاییکه هر متغیر معمولاً میتواند بیش از یک مقدار بپذیرد، حداکثرایندکسی که از بررسی هر مقدار بیرون میآید را پرش امن مینامیم و این دقیقاً زمانی است که الگوریتم گشینگ پرش مینماید.
در عمل این الگوریتم همزمان مشغول انجام محاسبههای گفته شده در بالا و نیز بررسی کردن سازگاری xk+1=ak+1 است.
پسپرش در گرههای داخلی[ویرایش]
در قسمت قبل روش کار الگوریتم برای زمانهایی که شاخهٔ دیگری وجود ندارد و زمانیکه مقادیر یک متغیر به صورت نامتناسب در انتهای شاخه بود را مورد بررسی قراردادیم. در روش قبلی به هنگام جستجوی درخت زمانی اجازه پسپرش داده میشد که در گرههای برگ قرارمیداشتیم و گره دیگری وجود نمیداشت.
یک گره داخلی از درخت جستجو نشان دهنده تخصیص یک متغیر است که سازگار با قبلی. اگر گره مناسب برای و حائز شرایطی برای پسپرش پیدا نشد از روش پسگرد استفاده میشود.
گرههای درونی در پسپرش نمیتوانند همانند حرکتی که در برگهای انتهایی یک درخت انجام میگرفت را انجام بدهند. اگر درجایی محاسبه xk+1 نیازمند حرکت در شاخهها شد این به این خاطر است متغیر اختصاص داده شده مناسب است و از همین متغیر میتوان برای مقایسهها استفاده نمود. در نتیجه گشتن به دنبال پیشوندی که با مقادیر متغیر انتخاب شده نامناسب باشد هرگز به عنوان گره مناسب شناخته نمیشود.
در این جور مواقع الگوریتم متوجه شدهاست که مقادیر xk+1=ak+1 راه حل را برای موضوع مورد نظر به ارمغان نمیآورد و موضوع به جستجوی بازگشتی از سری x1,…،xk تبدیل میشود. در واقع الگوریتم میداند که هیچ راه حلی در این نقط وجود ندارد که به حل کل موضوع کمک کند زیرا به جای خاتمه دادن، مجدداً به همین نقطهای که در حال حاضر قرار داد برخواهد گشت و دچار حلقه بیانتها میگردد.
این بازگشت مربوط است به تعداد بنبستها و نقاطی که الگوریتم آنهارا به عنوان نقاط نامناسب و خارج از راه حل شناسایی کردهاست. برای پسپرشهای بلندتر این الگوریتم نیازمند شناسایی این بنبستها است تا برای رسیدن به جواب مسئله از این بنبستها دوری کند. در واقع پرشهای امن ایندکسگذاری شدهاند و پسوندهایی که از نقاط کور متمایز شدهاند.
به عبارت دیگر زمانیکه همه مقادیر xk+1 مورد آزمون قرار گرفت، الگوریتم توانایی پسپرش به متغیری همچون xi را دارد به شرط آنکه ارزیابی سری xk+1,xk+2,… در برگهایی که بچههای گره xk+1 هستند نامناسب باشد. سری حرا همچنان x1,…،xi در نظر بگیرید.
سادهسازیها[ویرایش]

به منظور سادهسازی حجم عظیمی از گرههایی که در زیر درخت xk+1 وجود دارند، اطلاعات ضروری برای پسپرش امن در زمان بازدید از زیر درخت گره xk+1 جمعآوری میشود. پیدا کردن یک پرش امن را میتوان توسط دو ملاحظات ساده شده انجام داد. اولین موضوع، الگوریتم نیازمند پرش امن است اما لزوماً به دنبال بلندترین پرش امن ممکن نیست.
موضوع دوم این است که گرههای موجود در زیر درخت xl که از آنها با استفاده از پسپرش پریدیم را میتوان بهطور کامل نادیده بگیریم. به صراحت میتوان گفت تمام گرههایی در مسیر خانه xm تا خانه xl هستند نامرتبط با زیر درخت xm هستند؛ بنابراین میتوان تمامی گرههای این زیر مجموعه را نادیده گرفت.
در واقع اگر در این الگوریتم از گره xl تا xm به سمت پایین حرکت کردیم و در بین راه مجبور به پرش به عقب شدیم، میتوانیم مستقیماً به گره xm مراجعت نماید. در واقع در اینجا پرش به عقب بیانگر این نکتهاست که گرههایی که فیمابین گرههای xl و xm هستند کاملاً نامرتبط اند به زیر درخت گره xm. به عبارت دیگر پرش به عقب نشان دهنده این نکتهاست که بازدیداز یک ناحیه درخت جستجو میتوانسته کاملاً اشتباه باشد؛ بنابراین این قسمت از درخت جستجو میتواند کاملاً نادیده گرفته شود و پرش به گره xl ویا والدهای بالاتر گره والد اتفاق بیفتد

در هرگره میتوان از این نکته برای جمعآوری مجموعهای از اطلاعات بخصوص یافتن متغیرهای پیشین اختصاص داده شده به منظور اثبات این نکته که هیچ راه حلی در زیر درخت گره مورد نظر وجود ندارد استفاده نمود. این مجموعه جمعآوری اطلاعات در زمان اجرای الگوریتم ساخته میشود. زمانیکه از یک گره برگشت به عقب میکنیم مجموعه تمام متغیرهای آن گره و اطلاعات جمعآوری شده دربارهٔ آن گره که مقصد پسپرش یا مقصد Backtrack آن کجا بودهاست کاملاً حذف میشود. این اتفاق از آنجایی رخ میدهد که گرههای پرش شده از پسپرش هرگز شانس بازدید شدن را نخواهند داشت بنابراین این گرهها خودکار حذف میشوند.
پسپرشهای بر پایه گراف[ویرایش]
منطق این نوع پرش به عقب که در گرافها بکار برده میشود به این صورت است که یک پرش امن میتواند به وسیلهٔ چک کردن این نکته که کدام متغیر از سری x1,…،xk تناسب دارد با متغیرهای xk+1,xk+2,… که توسط گرههای برگ معرفی میشوند. برای هر گره برگ و هر متغیر xi ی که ایندکسهای i> نامناسب ناخته شدهاند، ایندکسهایی که کوچکتر یا مساوی k که در محدوده xi هست میتواند به عنوان محلی برای پیدا کردن پرش امن از آنها استفاده نمود. به صورت دقیقتر، زمانیکه تمامی مقادیر برای xk+1 مورد بررسی قرار گرفت مجموعهای از ایندکسهای متغیرهایی که باعث به وجود آمدن راه حل نهایی نمیشود شناسایی شده و بنابراین این نتیجه گرفته میشود که از ملاقات زیر درخت xk+1 هیچ راه حل قابل توجهی بدست نخواهد آمد. در این مواقع الگوریتم میتواند پرش به عقب به باارزشترین ایندکس موجود در مجموعه را انجام دهد.
از طریق الگوریتم زیر میتوان بهطور کامل زمان استفاده از پسپرش از گرههایی که بازدید نکردیم و این گرهها را کنار گذاشتهایم را بهطور کامل متوجه شوید: زمانیکه از یک گره به عقب بازمیگردیم مجموعهای از متغیرها که درمحدودیت خود این گره و فرزندان آن وجود دارند و حتی والد والدین گره میتوانند به عنوان کاندیدهای گره مقصد برای پرش مطرح شوند. در هر گره داخلی، مجموعهای از متغیرها حفظ شدهاست. هر زمان که مجموعهای از متغیرها از یکی از فرزندان یا نوادگان دریافت شد، این اطلاعات به مجموعه والد برای نگهداری بازگردانده میشود. زمانیکه نیاز به پسپرش یا پسگرد از گرهای نیاز بود، متغیرهای آن گره از لیست این مجموعه حذف میشوند و این اطلاعات به گره مقصدی که به آن حرکت میکنیم تحویل داده میشود. الگوریتم این رفتار را انجام میدهد برای اینکه مجموعهای را که در گره وجود دارد حاوی متغیرهایی است که در طول بررسی آن گره جمعآوری شدهاست و این اطلاعات حاوی نتایج با ارزشی در مورد گرههای زیر دست است. یه این خاطر است که تنها زمانیکه پرش به عقب اتفاق میفتدمجموعه متغیرها ارسال میشوند به گره مقصد، از این رو است که اطلاعات مربوط به گرهای که از آن پرش شده قابل چشمپوشی است.
کشمکشهای احتمالی در پسپرش[ویرایش]
همچنین یک روش بهینه شده در این الگوریتم وجود دارد که بعضی وقتها میتواند به پرشهای بسیار بلندتری دست یابد. این کار تنها با بررسی دو متغیر پیش رو در محدوده انجام نمیشود بلکه با بررسی اینکه آیا مانعی باعث نامناسب شناخته شدن یک گره شدهاست یا خیر نیز قابل انجام است. این الگوریتم یک عامل بنبست در گره را شناسایی میکند. در هر گره بزرگترین ایندکس یک متغیر که در یکی از نقاط برگها شناسایی شده باشد به عنوان گره امن پرش محسوب میشود.
خانههای نامناسب شناسایی شده در هر برگ امنیت نتیجه پرش را بسیار بالا میبرند، از همین رو انتخاب کردن مناسبترین ایندکس، احتمال پرشهای بلنتر را بشدت افزایش میدهد. به همین خاطر است که در این روش پرش به عقب، ترتیب خانههای نامناسب و دارای ارزش پایینتر هرگز بر خانههای دارای درجه و اهمیت بالاتر ترجیح داده نمیشود.
بعبارت دیگر، خانه یک گراف نسبت به خانه ترجیح داده میشود اگر بزرگترین ایندکس متغیر C پایینتر باشد از بزرگترین ایندکس متغیر D. در واقع به هنگام مواجه با متغیرهای مشترک، آن خانه از گراف انتخاب میشود که از ایندکسهای کوچکتری نسبت به سایرین برخوردار باشد.
الگوریتم در گرههای برگ، کوچکترین ایندکس مثل را با آخرین ایندکس مورد ارزیابی قرارمیدهد تا از این راه خانه نامناسب را شناسایی کند. ازبین خانههای با ارزش شناسایی شده شروع به مقایسه ایندکسهای مجموعهx برای انتخاب بهترین خانه میکند. به این ترتیب، زمانیکه الگوریتم مجدداً بازمیگردد به متغیر xk+1، کمترین ایندکس جمعآوری شده بیانگر پرش امن است.
در عمل این الگوریتم به وسیلهٔ جمعآوری تمام ایندکسها ساده در یک مجموعه واحد و در واقع به جای تولید کردن لیستهای مجزابرای هر سازی میشود به صورت خاص تر این الگوریتم در هر گره به جمعآوری همه مجموعههایی که از فرزندانش به هنگام پرش به عقب جمعآوری کردهاست میپردازد. زمان پرش به عقب از این گره، این مجموعه حذف میشود و تمامی اطلاعاتی که تا به حال جمعآوری کرده به هنگام پرش به عقب یا بازگشت به عقب را به خانه مقصد تحویل میدهد.
این روش پرش به عقب توسط پتریک پراسر (Patrick Prosser) در سال ۱۹۹۳ برای مطلوبسازی مشکلات زمان بنبست ارائه شدهاست.
جستارهای وابسته[ویرایش]
- آموزش محدودیت
منابع[ویرایش]
- Dechter, Rina (2003). Constraint Processing. Morgan Kaufmann. ISBN 1-55860-890-7.
- Prosser, Patrick (1993). "Hybrid Algorithms for the Constraint Satisfaction Problem" (PDF). Computational Intelligence 9(3). Archived from the original (PDF) on 6 February 2012. Retrieved 29 June 2011.
{{cite journal}}: Cite journal requires|journal=(help)