مرتب‌سازی شانه‌ای

مرتب‌سازی شانه‌ای

رده	الگوریتم مرتب‌سازی
ساختمان داده	آرایه
کارایی بدترین حالت	$\Omega (n^{2})$
کارایی بهترین حالت	$O(n)$
کارایی متوسط	$\Omega (n^{2}/2^{p})$, که p رقم افزایش است
پیچیدگی فضایی	$O(1)$

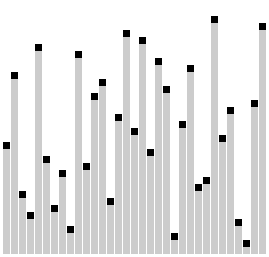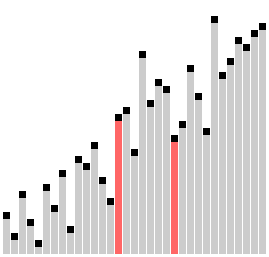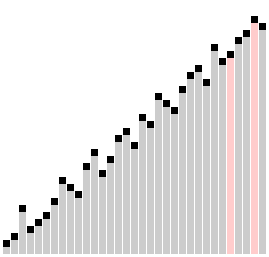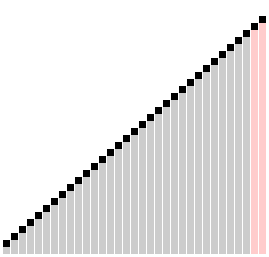
مرتب‌سازی شانه‌ای (به انگلیسی: Comb sort) یک الگوریتم مرتب‌سازی ساده است که توسط ولادیمیر دوبوسوویچ در سال ۱۹۸۰ طراحی شد. بعدها این الگوریتم در اثر مقاله‌ای که توسط استیفن لیسی و ریچارد باکس در سال ۱۹۹۱ در مجله بایت منتشر شد معروفیت پیدا کرد. مرتب‌سازی شانه‌ای بهینه شده‌ای از مرتب‌سازی حبابی است. ایدهٔ اصلی حذف لاک‌پشت ها، یا مقادیر کوچک نزدیک پایان است، که در مرتب‌سازی حبابی سرعت الگوریتم را به شدت پایین می‌آورند. (خرگوش‌ها مقادیر بزرگ نزدیک ابتدا مشکل حادی در مرتب‌سازی حبابی ایجاد نمی‌کنند).

در مرتب‌سازی حبابی وقتی که هر دو عنصری مقایسه شوند همیشه شکاف ۱ دارند، ایده اصلی مرتب‌سازی شانه‌ای این است که شکاف بیشتر از یک می‌تواند باشد.

شکاف وقتی شروع می‌شود که طول لیست توسط عامل چروک تقسیم می‌شود و لیست طبق آن مقدار برای شکاف مرتب می‌شود. سپس شکاف دوباره تقسیم بر عامل چروک می‌شود؛ و پروسه تا جایی ادامه می‌یابد که شکاف برابر ۱ شود. در این مرحله مرتب‌سازی شانه‌ای با استفاده از شکاف ۱ تا پایان مرتب شدن تمام لیست ادامه می‌دهد. مرحله پایانی مرتب‌سازی شانه‌ای شبیه مرتب‌سازی حبابی است، ولی اینجا بیشتر لاک‌پشت‌ها حل شده‌اند بنابراین بسیار کارآمدتر از مرتب‌سازی حبابی عمل می‌کند.

عامل چروک

عامل چروک اثر بسیار زیادی بر بازده مرتب‌سازی شانه‌ای دارد. در مقاله اصلی مولفان ۱٫۳ را پس از بررسی لیست‌های تصادفی زیادی پیشنهاد کرده‌اند؛ ولی پس از آن مشخص شد که استفاده از $1/\left(1-{\frac {1}{e^{\varphi }}}\right)\approx 1.247330950103979$ نتیجه بهتری خواهد داد.

تغییرپذیری‌ها

با استفاده از عامل چروک ۱٫۳ تنها سه راه ممکن برای شکاف‌ها برای اتمام وجود دارد: (۹, ۶, ۴, ۳, ۲, ۱)،(۱۰, ۷, ۵, ۳, ۲, ۱)،(۱۱, ۸, ۶, ۴, ۳, ۲, ۱). آزمایش‌های نشان می‌دهد که بهبودهای عمده می‌تواند حاصل شود اگر شکاف بر ۱۱ تنظیم شود.

پیاده‌سازی

شبه کد مرتب‌سازی شانه‌ای

    gap := input.size //initialize gap size

    loop until gap <= 1 and swaps = 0
        //update the gap value for a next comb. Below is an example
        gap := int(gap / 1.25)

        i := 0
        swaps := 0 //see مرتب‌سازی حبابی for an explanation

        //a single "comb" over the input list
        loop until i + gap >= input.size //see مرتب‌سازی شل for similar idea
            if input[i] > input[i+gap]
                swap(input[i], input[i+gap])
                swaps := 1 // Flag a swap has occurred, so the
                           // list is not guaranteed sorted
            end if
            i := i + 1
        end loop

    end loop
end function

پیاده‌سازی در ++C

template<class ForwardIterator>
void combsort ( ForwardIterator first, ForwardIterator last )
{
    static const double shrink_factor = 1.247330950103979;
    typedef typename std::iterator_traits<ForwardIterator>::difference_type difference_type;
    difference_type gap = std::distance(first, last);
    bool swaps = true;

    while ( (gap > 1) || (swaps == true) ){
        if (gap > 1)
            gap = static_cast<difference_type>(gap/shrink_factor);

        swaps = false;
        ForwardIterator itLeft(first);
        ForwardIterator itRight(first); std::advance(itRight, gap);
        
        for ( ; itRight!=last; ++itLeft, ++itRight ){
            if ( (*itRight) < (*itLeft) ){
                std::iter_swap(itLeft, itRight);
                swaps = true;
            }
        }
    }
}

پیاده‌سازی در جاوا

public static <E extends Comparable<? super E>> void sort(E[] input) {
    int gap = input.length;
    boolean swapped = true;
    while (gap > 1 || swapped) {
        if (gap > 1) {
            gap = (int) (gap / 1.3);
        }
        int i = 0;
        swapped = false;
        while (i + gap < input.length) {
            if (input[i].compareTo(input[i + gap]) > 0) {
                E t = input[i];
                input[i] = input[i + gap];
                input[i + gap] = t;
                swapped = true;
            }
            i++;
        }
    }
}

جُستارهای وابسته

• مرتب‌سازی حبابی، الگوریتمی کندتر که پایهٔ مرتب‌سازی شانه‌ای است.

پیوند به بیرون

• الگوریتم‌های مرتب‌سازی-مرتب‌سازی شانه‌ای

منابع

• Demuth, H. Electronic Data Sorting. PhD thesis, Stanford University, 1956.
• دانلد کنوت, هنر برنامه‌نویسی رایانه, Volume 3: Sorting and Searching.