زنجیره ایده‌آل

در شیمی پلیمر، یک زنجیره ایده آل (یا زنجیره با اتصال آزاد) ساده ترین مدل برای توصیف پلیمرها، مانند اسیدهای نوکلئیک و پروتئین ها است. فرض بر این است که مونومرهای یک پلیمر در مراحل یک واکر تصادفی فرضی قرار دارند که مراحل قبلی خود را به خاطر نمی آورد. با نادیده گرفتن برهمکنش‌های بین مونومرها، این مدل فرض می‌کند که دو (یا چند) مونومر می‌توانند مکان یکسانی را اشغال کنند. اگرچه ساده است، اما عمومیت آن بینشی در مورد فیزیک پلیمرها می دهد.

در این مدل مونومرها میله های صلب با طول ثابت l هستند و جهت گیری آنها کاملاً مستقل از جهت گیری و موقعیت مونومرهای همسایه است. در برخی موارد، مونومر یک تفسیر فیزیکی دارد، مانند اسید آمینه در یک پلی پپتید. در موارد دیگر، یک مونومر صرفاً بخشی از پلیمر است که می تواند به عنوان یک واحد گسسته و آزادانه مدل شود. اگر چنین است، l طول کوهن است. برای مثال، کروماتین به عنوان یک پلیمر مدل‌سازی می‌شود که در آن هر مونومر قطعه‌ای به طول تقریبی 14-46 کیلوبیت بر ثانیه است.[2]

مدل زنجیره ایده‌آل

N مرها پلیمر را تشکیل می دهند که طول کل بازشده آن برابر است با:

$L=Nl$، در حالی که $N$ تعداد مرها می‌باشد.

در این رویکرد بسیار ساده که هیچ برهمکنشی بین مرها در نظر گرفته نمی‌شود، انرژی پلیمر مستقل از شکل آن در نظر گرفته می‌شود، به این معنی که در تعادل ترمودینامیکی،با توجه به توزیع ماکسول-بولتزمن، در هنگام نوسان پلیمر همه شکل‌گیری‌های آن به یک اندازه احتمال رخ دادن دارد.

فرض کنید ${\vec {R}}$ را بردار انتها به انتها کل یک زنجیره ایده آل و ${\vec {r_{1}}},{\vec {r_{2}}},...,{\vec {r_{n}}}$ را بردارهای مربوط به مرهای منفرد بنامیم. این بردارهای تصادفی دارای اجزایی در سه جهت فضا هستند. اکثر عبارات ارائه شده در این مقاله فرض می کنند که تعداد مرها (N) زیاد است، بنابراین قضیه حد مرکزی می‌تواند اعمال شود. شکل زیر طرحی از یک زنجیره ایده آل (کوتاه) را نشان می دهد.

دو سر زنجیر بر هم منطبق نیستند، اما در اطراف یکدیگر در نوسان هستند، به‌طوری که البته:

$$\langle {\vec {R}}\rangle =\Sigma _{i=1}^{N}\langle {\vec {r}}_{i}\rangle ={\vec {0}}~$$

در سراسر مقاله از براکت‌های $\langle \rangle$ برای نشان دادن میانگین (مقادیر گرفته شده در طول زمان) یک متغیر تصادفی یا یک بردار تصادفی، مانند بالا استفاده می شود.

از آنجایی که ${\vec {r}}_{1},\ldots ,{\vec {r}}_{N}$ مستقل آماری است، از قضیه حد مرکزی نتیجه می‌شود که ${\vec {R}}$ بر اساس یک توزیع نرمال (یا توزیع گاوسی) توزیع می شود: دقیقاً، در سه بعدی، $R_{x},R_{y}$ و $R_{z}$ بر اساس توزیع نرمال با میانگین 0 توزیع می شوند. و واریانس آنها طبق روابط زی محاسبه می‌شود:

$$\sigma ^{2}=\langle R_{x}^{2}\rangle -\langle R_{x}\rangle ^{2}=\langle R_{x}^{2}\rangle -0$$$$\langle R_{x}^{2}\rangle =\langle R_{y}^{2}\rangle =\langle R_{z}^{2}\rangle =N\,{\frac {l^{2}}{3}}$$

به طوری که $\langle {\vec {R^{2}}}\rangle =N\,l^{2}=L\,l~$. بردار انتها به انتهای زنجیره بر اساس تابع چگالی احتمال زیر توزیع می شود:

$$P({\vec {R}})=\left({\frac {3}{2\pi Nl^{2}}}\right)^{3/2}e^{-{\frac {3{\vec {R}}^{2}}{2Nl^{2}}}}$$مقداری که اغلب در فیزیک پلیمر استفاده می شود شعاع چرخش است:

$${\mathit {R}}_{G}={\frac {{\sqrt {N}}\,l}{{\sqrt {6}}\ }}$$شایان ذکر است که فاصله انتها به انتها متوسط ​​بالاتر، که در مورد این مدل ساده، دامنه نوسانات سیستم نیز می باشد، در مقایسه با کل طول بازشده پلیمر در حدود ترمودینامیکی ناچیز می شود. این نتیجه یک ویژگی کلی سیستم های آماری است. نکته ریاضی: نشان دادن دقیق بیان چگالی احتمال $P({\vec {R}})$ آنقدر که در بالا به نظر می رسد مستقیم نیست: از اعمال قضیه حد مرکزی معمول (1D) می توان نتیجه گرفت که $R_{x},R_{y}$ و $R_{z}$ بر اساس یک نرمال با واریانس $N\,l^{2}/3$ توزیع شده‌اند. سپس، عبارت فوق برای $P({\vec {R}})$ تنها موردی نیست که با چنین توزیعی برای $R_{x},R_{y}$ و $R_{z}$ سازگار است. با این حال، از آنجایی که اجزای بردارها ${\vec {r}}_{1},\ldots ,{\vec {r}}_{N}$ برای ولگشت مورد نظر ما همبستگی ندارند، نتیجه می شود که $R_{x},R_{y}$ و $R_{z}$ نیز نامرتبط هستند. این شرط اضافی تنها در صورتی محقق می شود که ${\vec {R}}$ مطابق $P({\vec {R}})$ توزیع شود. از طرف دیگر، این نتیجه را می توان با اعمال تعمیم چند بعدی قضیه حد مرکزی یا از طریق استدلال های تقارن نشان داد.

کلیت مدل

در حالی که مدل ابتدایی شرح داده شده در بالا کاملاً با توصیف پلیمرهای دنیای واقعی در مقیاس میکروسکوپی سازگار نیست، در مقیاس ماکروسکوپی در مورد پلیمری در محلول که مونومرهای آن ترکیب ایده آلی را با حلال تشکیل می دهند، ارتباطی را نشان می دهد. در این صورت، برهمکنش‌های بین مونومر و مونومر، مولکول حلال و مولکول حلال، و بین مونومر و حلال یکسان هستند و انرژی سیستم را می‌توان ثابت در نظر گرفت و فرضیه‌های مدل را تأیید می‌کند.

ارتباط مدل، با این حال، محدود است، حتی در مقیاس ماکروسکوپی، با این واقعیت که هیچ حجم استثنایی برای مونومرها در نظر نمی گیرد (یا، به عبارت شیمیایی، که از اثرات فضایی غفلت می کند). از آنجایی که Nmerها دارای طول صلب و ثابت هستند، این مدل کشش پیوند را نیز در نظر نمی‌گیرد، اگرچه می‌توان آن را برای انجام این کار گسترش داد.

سایر مدل‌های پلیمری نوسانی که هیچ برهم‌کنشی بین مونومرها و حجم حذف شده را در نظر نمی‌گیرند، مانند مدل زنجیره‌ای کرم‌مانند، همگی به‌طور مجانبی نسبت به این مدل در حدود ترمودینامیکی همگرا هستند. برای این قیاس یک قطعه کوهن معرفی شده است که مربوط به طول مونومر معادل است که در زنجیره ایده آل مشابه در نظر گرفته می شود. تعداد قطعات کوهن که باید در زنجیره ایده آل مشابه در نظر گرفته شوند برابر است با کل طول بازشده پلیمر تقسیم بر طول یک قطعه کوهن.

کشش آنتروپیک یک زنجیره ایده آل

اگر دو انتهای آزاد یک زنجیره ایده آل توسط نوعی وسیله از هم جدا شوند، آنگاه دستگاه نیرویی را که توسط پلیمر وارد می شود، تجربه می کند. همان‌طور که زنجیره ایده آل کشیده می شود، انرژی آن ثابت می ماند و میانگین زمانی یا انرژی درونی آن نیز ثابت می ماند، به این معنی که این نیرو لزوما از یک اثر آنتروپیک صرف نشات می گیرد.

این نیروی آنتروپیک بسیار شبیه فشاری است که دیواره های جعبه حاوی گاز ایده آل تجربه می کنند. انرژی داخلی یک گاز ایده آل فقط به دمای آن بستگی دارد، نه به حجم جعبه حاوی آن، بنابراین این یک اثر انرژی نیست که مانند فشار گاز، حجم جعبه را افزایش دهد. این نشان می دهد که فشار یک گاز ایده آل منشا آنتروپیکی دارد.

منشا میکروسکوپی چنین نیرو یا فشار آنتروپیک چیست؟ کلی ترین پاسخ این است که اثر نوسانات حرارتی تمایل دارد یک سیستم ترمودینامیکی را به یک حالت ماکروسکوپی برساند که مطابق با حداکثر تعداد حالت های میکروسکوپی (یا حالت های ریز) است که با این حالت ماکروسکوپی سازگار است. به عبارت دیگر، نوسانات حرارتی تمایل دارند یک سیستم را به حالت ماکروسکوپی حداکثر آنتروپی خود برسانند.

این در مورد زنجیره ایده آل به چه معناست؟ اول، برای زنجیره ایده آل ما، یک حالت میکروسکوپی با برهم نهی حالت های ${\vec {r}}_{i}$ از هر مونومر مشخص می شود (با I از 1 تا N متغیر است). در حلال خود، زنجیره ایده‌آل دائماً در معرض شوک‌های ناشی از حرکت مولکول‌های حلال است و هر یک از این شوک‌ها سیستم را از حالت میکروسکوپی فعلی به حالت میکروسکوپی بسیار مشابه دیگری می‌فرستد. برای یک پلیمر ایده‌آل، همان‌طور که در زیر نشان داده خواهد شد، حالت‌های میکروسکوپی بیشتری وجود دارد که با فاصله انتها به انتها کوتاه سازگار هستند تا حالت‌های میکروسکوپی سازگار با فاصله انتها به انتها زیاد. بنابراین، برای یک زنجیره ایده آل، به حداکثر رساندن آنتروپی آن به معنای کاهش فاصله بین دو انتهای آزاد آن است. در نتیجه، نیرویی که تمایل به فروپاشی زنجیره دارد، توسط زنجیره ایده آل بین دو انتهای آزاد آن اعمال می شود.

زنجیره ایده آل تحت یک محدودیت نیروی ثابت

A diagram of an ideal chain constrained by a constant force.

یک زنجیره آزاد از پیوند N به طول $l$ را در نظر بگیرید که تحت یک نیروی کششی ثابت f به انتهای آن در امتداد محور $z$ و دمای محیط $T$ اعمال می شود. یک مثال می تواند زنجیره ای با دو بار مخالف +q و -q در انتهای آن در یک میدان الکتریکی ثابت ${\vec {E}}$ باشد که در امتداد محور $z$ همان‌طور که در شکل سمت راست ترسیم شده است. اگر برهمکنش مستقیم کولن بین بارها نادیده گرفته شود، نیروی ثابت ${\vec {f}}$ در دو انتها وجود دارد.

ترکیب‌های زنجیره‌ای مختلف به یک اندازه محتمل نیستند، زیرا با انرژی متفاوت زنجیره در میدان الکتریکی خارجی مطابقت دارند.

$U=-q{\vec {E}}\cdot {\vec {R}}=-{\vec {f}}\cdot {\vec {R}}=-fR_{z}$

بنابراین، ترکیب زنجیره های مختلف دارای فاکتورهای آماری بولتزمن $exp(-U/k_{B}T)$ متفاوت است.

تابع پارتیشن به شکل زیر است:

$Z=\sum _{\text{states}}\exp(-U/k_{B}T)=\sum _{\text{states}}\exp \left({fR_{z} \over k_{B}T}\right)$

هر اتصال مونومر در زنجیره با بردار ${\vec {r_{i}}}$ به طول $l$ و زاویه $\theta _{i},\varphi _{i}$ مشخص می شود.

در سیستم مختصات کروی بردار انتها به انتها را می توان به صورت زیر نشان داد: $R_{z}=\sum _{i=1}^{N}l{\text{ }}\cos \theta _{i}$

از این رو:

${\begin{aligned}Z=&\int \exp({fl \over k_{B}T}\sum _{i=1}^{N}\cos \theta _{i})\prod _{i=1}^{N}\sin \theta _{i}d\theta _{i}d\varphi _{i}=\\&\left[\int _{0}^{\pi }2\pi {\text{ }}\sin \theta _{i}{\text{ }}\exp \left({fl \over k_{B}T}\cos \theta _{i}\right)\,d\theta _{i}\right]^{N}=\\&\left[{2\pi \over fl/(k_{B}T)}\left(\exp \left({fl \over k_{B}T}\right)-\exp \left(-{fl \over k_{B}T}\right)\right)\right]^{N}=\\&\left[{4\pi {\text{ }}\sinh(fl/(K_{B}T)) \over fl/(k_{B}T)}\right]^{N}\end{aligned}}$

انرژی آزاد گیبس G را می توان مستقیماً از تابع پارتیشن محاسبه کرد:

$G(T,f,N)=-k_{B}T{\text{ }}\ln {\text{ }}Z(T,f,N)=-Nk_{B}T\left[\ln \left(4\pi {\text{ }}\sinh \left({fl \over k_{B}T}\right)\right)-\ln \left({fl \over k_{B}T}\right)\right]$

انرژی آزاد گیبس در اینجا مورد استفاده قرار می گیرد زیرا مجموعه زنجیره ها با دمای ثابت $T$ و نیروی ثابت $f$ مطابقت دارد (مشابه با مجموعه همدما-ایزوباریک که دما و فشار ثابتی دارد).

میانگین فاصله انتها به انتها مربوط به یک نیروی معین را می توان به عنوان مشتق انرژی آزاد به دست آورد:

$\langle R\rangle =-{\partial G \over \partial f}=Nl\left[\coth \left({fl \over k_{B}T}\right)-{k_{B}T \over fl}\right]$

این عبارت همان تابع Langevin ${\mathcal {L}}$ است.

The average distance $\left\langle {\vec {R}}\right\rangle$ of the chain as a function of $\alpha$.

${\mathcal {L}}(\alpha )=\coth(\alpha )-{1 \over \alpha }$

$\alpha ={fl \over k_{B}T}$.

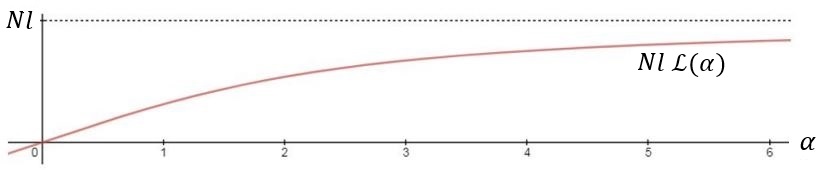
برای طول های نسبی کوچک ($\left\langle R\right\rangle \ll R_{max}=lN$) وابستگی تقریباً خطی است،

${\mathcal {L}}(\alpha )\cong {\alpha \over 3}$ for $\alpha \ll 1$

و همان‌طور که در پاراگراف های قبلی نشان داده شده است از قانون هوک پیروی می کند:

${\vec {f}}=k_{B}T{3\left\langle {\vec {R}}\right\rangle \over Nl^{2}}$

منابع

1. https://en.wikipedia.org/wiki/Ideal_chain
2. Polymer Physics ISBN 019852059-X, 76, Rubinstein
3. Ideal Chain Conformations and Statistics, Chinedum Osuji