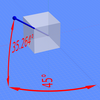
تصویر ایزومتریک
|
| |
تصویر ایزومتریک یک مکعب.
|
گردش ناظر مورد نیاز برای دست‌یابی به این پرسپکتیو.
|
تصویر ایزومتریک رایج‌ترین نوع تصویرسازی گرافیکی در علوم فنی‌مهندسی است و یکی از انواع تصویر آگزنومتریک به شمار می‌رود. برای رسم این تصویر، جسم به اندازهٔ ۴۵° در راستای محور عمودی‌اش چرخانده و تقریباً ۳۵٫۲۶۴° (دقیقاً به اندازهٔ ) به جلو مایل می‌شود. به این ترتیب زاویهٔ بین محورهای جسم در تصویر ۱۲۰° خواهد شد. در نتیجه تصویر در راستای هر سه محور دارای مقیاس یکسانی خواهد بود و نسبت اندازه‌ها حفظ می‌شود. بر اثر این نوع گردش جسم، نسبت اندازه‌ها در تصویر ۰٫۸۱۵برابر اندازه‌ها در جسم خواهد شد. برای مقاصد عملی که نیاز به اندازه‌گیری مستقیم است، آن را دوباره تا مقیاس ۱:۱ بزرگ می‌کنند.[۱]
در هنگام رسم تصاویر ایزومتریک باید توجه خاصی به انتخاب محورهای اصلی داشت تا بیشترین اطلاعات با یک جلوهٔ طبیعی و شهودی و با کمترین نیاز به رسم خطوط پنهان یا نماهای دیگر حاصل شود.[۲]
رسم تصاویر ایزومتریک امروزه معمولاً به کمک نرم‌افزارهای CAD انجام می‌شود. با این وجود رسم دستی نمای کلی ایزومتریک به‌ویژه در مراحل اولیهٔ طراحی می‌تواند مفید باشد و کاربرد دارد. برای رسم دستی تصاویر ایزومتریک می‌توان از کاغذ ایزومتریک که دارای خطوط شبکه‌ایِ موازی با محورهای اصلی تصویر (ژرفا، بلندا و پهنا) هستند استفاده کرد.[۳]
در تصاویر ایزومتریک، کلیهٔ خطوطی که با محورهای ایزومتریک موازی باشند، خطوط ایزومتریک خوانده می‌شوند که اندازه‌ها در آن‌ها حفظ می‌شود، اما کلیهٔ خطوط غیرایزومتریک در اندازهٔ واقعی خود ظاهر نمی‌شوند و رسمشان دشوارتر خواهد بود. با توجه به این نوع تغییرمقیاس اَشکال دایره‌ای جسم در تصویر به صورت بیضی ظاهر خواهند شد. با وجود تکنیک‌ها و ابزارهای مختلف، رسم بیضی‌ها می‌تواند دشوار باشد، برای جانمایی صحیح می‌توان از مربع/مستطیل محیطیِ دایره/بیضی برای یافتن محل دقیق قطر بزرگ‌تر آن و سپس رسم استفاده کرد. اشکال نامنظم دیگر نیز با تعریف یک شبکهٔ مربعی در سطح شکل و منتقل‌کردن نقاط تماس شکل با شبکه به شبکهٔ معادل در تصویر قابل رسم هستند.[۴]
جستارهای وابسته
[ویرایش]
پانویس
[ویرایش]- ↑ Alcaniz et al, Visualization and Engineering Design Graphics with Augmented Reality Second Edition:, 98.
- ↑ Alcaniz et al, Visualization and Engineering Design Graphics with Augmented Reality Second Edition:, 98.
- ↑ Alcaniz et al, Visualization and Engineering Design Graphics with Augmented Reality Second Edition:, 100.
- ↑ Alcaniz et al, Visualization and Engineering Design Graphics with Augmented Reality Second Edition:, 102.
منابع
[ویرایش]- Alcaniz, M.; Camba, J.D.; Contero, M.; Otey, J. (2014). Visualization and Engineering Design Graphics with Augmented Reality Second Edition: (به انگلیسی). Schroff Development Corporation. Retrieved 2015-04-05.