نسبیت خاص
| نوشتاری از مجموعه |
| نسبیت خاص |
|---|
 |
نسبیت خاص (به انگلیسی: (SR)Special Relativity) نظریهای فیزیکی دربارهٔ اندازهگیری در چارچوب مرجع لخت است که در سال ۱۹۰۵ میلادی توسط آلبرت اینشتین در نوشتاری با نام «درباب الکترودینامیک و حرکت اجسام» مطرح شد.(مطالعه پدیده ها در تندی های بسیار زیاد و قابل مقایسه با تندی نور)[۱]
| بخشی از سری مقالات در مورد: |
| نسبیت عام |
|---|
 |
گالیلئو گالیله قبلاً چنین اصلی را بیان نموده بود که تمام حرکات یکنواخت نسبی هستند و هیچ حالت سکون مطلق و تعریف شدهای وجود ندارد (چارچوب مرجع برتر وجود ندارد). این اصل امروزه اصل نسبیت گالیله خوانده میشود. انیشتین این اصل را با در نظرگرفتن پدیده سرعت ثابت نور گسترش داد؛ پدیدهای که به تازگی در آزمایش مایکلسون-مورلی مشاهده شده بود.[۲] او همچنین بیان نمود که این اصل برای تمام قوانین فیزیک صادق است که در آن زمان شامل قوانین مکانیک و الکترودینامیک میشد.[۳] این نظریه پیامدهای گستردهای دارد که مورد تأیید دادههای تجربی قرار گرفتهاند[۴] و شامل موضوعاتی غیر شهودی همچون انقباض طول، اتساع زمان و نسبیت همزمانی است. او مفهوم کلاسیک بازه زمانی ناوردا برای دو رویداد را با مفهوم ناوردایی بازه فضازمان تعویض کرد. میتوان با استفاده از دو اصل نسبیت خاص و ترکیب آنها با سایر قوانین فیزیک به همارزی جرم و انرژی بر طبق اصل همارزی جرم و انرژی (E = mc²) رسید که c در آن برابر با سرعت نور در خلأ است.[۵][۶] پیشبینیهای نسبیت خاص با مکانیک نیوتنی در قلمرو مشترکشان همخوانی دارند. به ویژه در مورد سرعتهایی که از سرعت نور بسیار کوچکتر هستند. تأثیر نسبیت خاص هنگام بررسی اجسام در حال حرکت با سرعتهای بسیار زیاد (نزدیک به سرعت نور) قابل توجه میشود؛ بنابراین نظریهٔ نسبیت همانطور که اصل همخوانی فیزیک ایجاب میکند باید نتایج مشاهدات قبلی را به شکل کامل تری بیان کند. مقایسه رابطه بین مکانیک نیوتنی و مکانیک نسبیتی همانند مقایسه بین تبدیلات لورنتس و تبدیلات گالیله است و میتوان مطلب فوق را به بیان ریاضی به شکل زیر نمایش داد:
(تبدیلات لورنتس) = (تبدیلات گالیله)
البته در نظر داشته باشید که هنگامی که c به سمت بینهایت میل میکند (همانگونه که پیش از اثبات متناهی بودن سرعت نور پنداشته میشد) کسر v/c به سمت صفر میرود. این بدان معناست که تبدیلات لورنتس که اساس نظریهٔ نسبیت خاص هستند در سرعتهای بسیار کم نسبت به نور، نتایج یکسانی را با معادلات گالیله که اساس نسبیت نیوتونی هستند به دست میدهند. نظریه نسبیت خاص به ما میگوید که c تنها سرعت یک پدیده مشخص نیست بلکه یکی از ویژگیهای بنیادی شیوهای است که فضا و زمان با یکدیگر به شکل فضا زمان یکپارچه گشتهاند. یکی از پیامدهای این نظریه است که ذرهای که جرم لختی دارد هرگز سرعتش به سرعت نور نمیرسد.
واژه خاص در نسبیت خاص نشانگر حالت خاصی است که این نظریه در آن صادق است. این نظریه اصل نسبیت را تنها در مورد ویژهٔ چارچوبهای مرجع لخت به کار بردهاست. به عبارت دیگر اینطور پنداشته شدهاست که چارچوبهای مرجع نسبت به یکدیگر با سرعت یکنواختی حرکت میکنند.[۷] انیشتین نسبیت عام را معرفی نمود و اصل نسبیت را در حالت کلی تری به کار گرفت تا برای هر چارچوبی که قادر به تغییر مختصات عمومی است، صادق باشد. این نظریه تأثیرات گرانشی را هم در نظر میگیرد.
این واژه امروزه کاربرد کلی تری پیدا کرده و برای ارجاع به هر موردی که در آن گرانش ناچیز است استفاده میشود. نسبیت عام تعمیمی بر نسبیت خاص است که گرانش را نادیده نمیگیرد. در نسبیت عام گرانش توسط هندسه نااقلیدسی توصیف میشود؛ به گونهای که تأثیرات گرانشی با خمش فضازمان نمایش داده میشوند. نسبیت خاص تنها به فضاهای تخت محدود است. همانگونه که خمش زمین در زندگی روزمره ناچیز به نظر میرسد خمش فضازمان نیز در مقیاسهای کوچک قابل صرف نظر کردن است و بنابراین به صورت محلی نسبیت خاص تقریب قابل قبولی از نسبیت عام است.[۸]
اصول[ویرایش]
بازتابهایی از این نوع برای من روشن ساخت که تا مدتی پس از سال ،۱۹۰۰ یعنی زمان کوتاهی بعد از کار پیشگامانه پلانک، نیز نه مکانیک و نه الکترودینامیک نمیتوانستند ادعای درستی دقیق (به جز در موارد خاص) داشته باشند. به تدریج من از امکان یافتن قوانین واقعی با استفاده از تلاشهای سازنده برپایه حقایق دانسته شده ناامید شدم. هر چه بیشتر و از جان گذشته تر تلاش مینمودم بیشتر به این باور نزدیک میشدم که تنها کشف یک اصل رسمی جهانشمول میتواند مارا به نتایج مطمئنی برساند… چگونه میشد چنین اصلی یافت؟
— آلبرت انیشتین: یادداشتهای اتوبیوگرافی [۹]

انیشتین دو پنداشت پایهای مطرح نمود که به نظر میرسید که بدون توجه به اعتبار قوانین شناخته شده - که در آن زمان یا مکانیکی یا الکترودینامیکی بودند - قابل اطمینان باشند. این پنداشتها ثابت بودن سرعت نور و دیگری استقلال قوانین فیزیکی (مخصوصا ثابت بودن سرعت نور) از دستگاه لخت انتخاب شده بود. در اولین ارائه نسبیت خاص در سال ۱۹۰۵، وی این اصول را به صورت زیر مطرح نمود:[۱]
- اصل نسبیت
قوانین فیزیک در تمام چارچوبهای لَخت یکسان هستند و هیچ چهارچوب لخت مرجعی وجود ندارد.
این اصل که پیش از نسبیت خاص در نسبیت نیوتونی نیز بودهاست بیان میکند که تمامی چهارچوبهایی که با سرعتی ثابت (بدون شتاب) حرکت میکنند هم ارز و یکسان هستند، بدین ترتیب هیچ چهارچوب لختی بر چهارچوب دیگر برتری یا با دیگری تفاوت ندارد.
به سخنی دیگر اصل نسبیت (با در نظر گرفتن یک شرایط ایدهآل) میگوید که اگر شما در آزمایشگاه سربستهای قرار داشته باشید و آن آزمایشگاه با سرعت ثابتی نسبت به زمین حرکت کند، شما با هیچ روشی نمیتوانید تعیین کنید که سرعتتان نسبت به زمین چقدر است. در این بیان از اصل نسبیت، فرض شدهاست که زمین یک چارچوب لخت است (این موضوع دربارهٔ زمین به تقریب صادق است)، همچنین فرض شدهاست که شما نسبت به زمین به نرمی حرکت میکنید و آزمایشگاه هیچ لرزش و تکانی ندارد.
- اصل سرعت ثابت نور
"نور همواره در فضای خالی با سرعت مشخص c منتشر میشود که مستقل از وضعیت حرکتی جسم منتشرکننده نور است " (از پیشگفتار)).[۱] این بدان معنی است که نور در خلأ، حداقل در یک دستگاه مختصات لخت (دستگاه ثابت) با سرعت c (مقداری ثابت که مستقل از جهت است) و بدون توجه به وضعیت حرکتی منبع نور منتشر میشود. سرعت نور در خلأ برای تمام ناظران لَخت ثابت و برابر c است و به حرکت چشمهٔ نور یا حرکت ناظر بستگی ندارد.
به سخنی دیگر اگر شما سوار اتومبیلی باشید که با سرعت ۵۰ کیلومتر بر ساعت حرکت میکند و اتومبیل دیگری با سرعت ۲۰ کیلومتر بر ساعت به شما نزدیک شود، سرعت نسبی اتومبیل شما و اتومبیل مقابل تقریباً برابر با ۷۰ کیلومتر بر ساعت خواهد بود، اما بر طبق این اصل اگر چشمهٔ نوری با سرعت دلخواهی به شما نزدیک شود و شما هم با سرعت متفاوتی به سمت آن چشمه حرکت کنید باز هم سرعت نور شما همان c خواهد بود. چنین چیزی کاملاً مخالف شهود روزمرهٔ ماست.
نسبیت خاص نه تنها بر این دو اصل آشکار بلکه بر چندین پنداشت ضمنی دیگر نیز وابسته است. از جمله این پنداشتها میتوان به همسانگردی و یکنواختی فضا و استقلال ساعتها و میلههای اندازهگیری از تاریخ گذشتهشان اشاره نمود.[۱۰]
به دنبال ارائه نخستین نسبیت خاص توسط انیشتین در سال ۱۹۰۵ مجموعههای متعددی از اصول پیشنهاد شدهاست.[۱۰] اما رایجترین مجموعه اصول همچنان همان اصولی هستند که توسط انیشتین در مقاله اصلی منتشر شدند. یک نسخه ریاضی از اصل نسبیت که بعدها توسط انیشتین ارائه شد عبارت است از:
اصل نسبیت خاص: اگر سیستم مختصات K برگزیده شود به گونهای که در ارتباط با آن قوانین فیزیک در سادهترین حالت خود به خوبی برقرار باشند، همان قوانین در ارتباط با هر دستگاه مختصات 'K دیگری نیز که در انتقال یکنواختی نسبت به K حرکت میکنند به خوبی صادق خواهند بود.[۱۱]
آنری پوانکاره با اثبات اینکه تبدیلات لورنتس زیرمجموعهای از گروه پوانکاره در تبدیلات تقارنی هستند، چارچوبی ریاضیاتی برای نظریه نسبیت ارائه داد. بعدها انیشتین این تبدیلات را از اصولی که ارائه داده بود استنتاج کرد.
بسیاری از مقالات انیشتین مشتقاتی از تبدیلات لورنتس بر پایه این دو اصل را نمایش میدهند.[۱۲]
انیشتین همواره استنتاج ناوردایی لورنتس (هسته اصلی نسبیت خاص) را تنها برپایه دو اصل نسبیت و ثابت بودن سرعت نور بنا نهادهاست. او اینچنین مینویسد:
بینش پایهای در نظریه نسبیت خاص این است: پنداشتهای نسبیت و ناوردایی سرعت نور در صورتی سازگار هستند که اصولی که برای تغییر مختصاتها و زمانهای رخدادها بنا میشوند روابطی از یک نوع جدید ("تبدیلات لورنتس") باشند… از اصل جهانی نظریه خاص نسبیت درون این اصل قرار دارد: قوانین فیزیک نسبت به تبدیلات لورنتس ناوردا هستند (برای انتقال از یک دستگاه لخت به هر دستگاه لخت دلخواه دیگری که مورد نظر باشد). این یک اصل محدودکننده برای قوانین طبیعی است…[۹]
از این روی بسیاری از شکلهای امروزی نظریه نسبیت تنها آن را بر پایه اصل جهانی هم وردایی لورنتس یا هم ارز آن یعنی اصل فضای مینکوفسکی، بنا مینهند.[۱۳][۱۴]
با استفاده از اصل نسبیت به تنهایی و بدون فرض ثابت بودن سرعت نور (یعنی با استفاده از همسانگردی فضا و تقارنی که از اصل نسبیت خاص نتیجه میشود) میتوان نشان داد که تبدیلات فضازمان بین چارچوبهای لخت یکی از سه نوع اقلیدسی، گالیلهای یا لورنتسی هستند. در مورد تبدیلات لورنتسی میتوان به پایستگی بازه نسبیتی و یک محدودیت سرعت متناهی به دست آورد. آزمایشها نشان میدهند که این حد سرعت برابر سرعت نور در خلأ میباشد.[۱۵][۱۶]
انگیزههایی که اندیشه ثابت بودن سرعت نور را به ارمغان آوردند، نظریه الکترومغناطیس ماکسول و نبود شواهد تجربی برای وجود اتر بودند. شواهد متناقضی در مورد اینکه تا چه حد انیشتین از نتیجه آزمایش آزمایش مایکلسون-مورلی تأثیر گرفته در دست است.[۱۷][۱۸] به هر ترتیب نتیجه آزمایش میکلسون-مورلی کمک کرد تا مفهوم ثابت بودن سرعت نور مورد پذیرش گسترده و سریعی قرار گیرد.
نبود چارچوب مرجع مطلق[ویرایش]
اصل نسبیت که بیان میدارد هیچ دستگاه مرجع لخت برتری وجود ندارد، در حقیقت به زمان گالیله برمی گردد و درون فیزیک نیوتنی نیز راه داشتهاست. اما در اواخر قرن نوزدهم وجود امواج الکترومغناطیسی فیزیکدانان را برآن داشت تا پیشنهاد دهند که جهان از مادهای به نام اتر پر شدهاست که همچون رسانهای عمل میکند که امواج و ارتعاشات از آن میگذرند. گمان میشد که اتر چارچوب مرجع مطلق است که سرعتها را میتوان بر اساس آن اندازه گرفت و خود آن بدون حرکت و ثابت است. خواص جالبی برای اتر پنداشته میشد: به اندازه کافی کشسان بود که بتواند امواج الکترومغناطیسی را پشتیبانی کند و این امواج میتوانستند با ماده برهم کنش داشته باشند، با این وجود اتر در مقابل گذر اجسام از خود مقاومتی نشان نمیداد. نتایج آزمایشهای مختلف و از جمله آزمایش مایکلسون-مورلی گویای این بودند که زمین همواره نسبت به اتر ثابت میماند. چیزی که توضیح آن مشکل بود زیرا زمین در مداری به دور خورشید میگردد. راه حل انیشتین این بود که مفهوم اتر و حالت سکون مطلق را کنار بگذارد. نسبیت خاص به گونهای فرمولبندی شده که هیچ چارچوب مرجعی را ویژه نمیداند؛ بلکه در نسبیت هر چارچوب مرجعی که با سرعت یکنواخت حرکت کند همین قوانین فیزیک را مشاهده خواهد کرد. بهطور ویژه سرعت نور در خلأ همواره در اندازهگیریها برابر c است، حتی وقتی که توسط چندین دستگاه مختلف که با سرعتهای متفاوت اما یکنواختی حرکت میکنند.
چارچوبهای مرجع، مختصاتها و تبدیلات لورنتس[ویرایش]

نسبیت بر پایه مفهوم «چارچوبهای مرجع» استوار است. در اینجا منظور از واژه چارچوب مرجع، یک ژرفانمایی (پرسپکتیو) مشاهدهای در فضاست که تغییری در حرکت آن رخ نمیدهد (شتاب ندارد) که از طریق آن میتوان یک موقعیت را در امتداد سه محور فضایی اندازه گرفت. افزون بر این یک چارچوب مرجع توانایی تعیین زمان رویدادها از طریق یک 'ساعت' (هر دستگاه مرجعی با تناوب یکنواخت) را دارد.
یک رویداد، اتفاقی است که میتوان یک زمان یکتا را به مکانی در فضا نسبت به یک چارچوب مرجع، نسبت داد: «نقطه» ای در فضازمان. از آنجاییکه سرعت نور در نسبیت در همه چارچوبهای مرجع ثابت است، میتوان از پالسهای نور برای اندازهگیری مطمئن فاصلهها و ارجاع به زمانهایی که رویدادها برای ساعت اتفاق افتادهاند استفاده نمود. اگرچه که برای نور همزمانی پس از شروع رویداد طول خواهد کشید تا به ساعت برسد.
مثلاً انفجار یک ترقه را میتوان یک «رویداد» در نظر گرفت. میتوان یک رویداد را با استفاده از چهار مختصات فضازمان آن مشخص نمود. زمان رویداد و مکان فضایی سه بعدی اش یک نقطه مرجع میسازند. این چارچوب مرجع را S مینامیم. در نسبیت اغلب به محاسبه موقعیت یک نقطه از یک نقطه مرجع دیگر علاقهمندیم. فرض کنید که چارچوب مرجع دومی به نام ′S داریم که محورهای فضایی و ساعتش با محورهای فضایی و ساعت S در زمان صفر همزمان و هممکان بودهاند، اما با سرعت ثابت v نسبت به S در امتداد محور ایکسها حرکت میکند.
از آنجا که در نظریه نسبیت هیچ چارچوب مرجع مطلقی وجود ندارد، مفهوم مؤکدی از «حرکت» نیز وجود ندارد زیرا همه چیز همواره نسبت به چارچوب مرجع دیگری در حرکت است. به جای آن هرگاه دو چارچوب مرجع که باسرعت یکسان در جهت یکسان حرکت کنند، به آن حرکت همراه گفته میشود؛ بنابراین S و′S حرکت همراه ندارند. برای رویدادها مختصات فضازمان (t,x،y,z) در دستگاه S و (′t′,x′,y′,z) در دستگاه ′S تعریف میکنیم. تبدیل لورنتس بیان میکند که این دو مختصات به شیوه زیر در ارتباط هستند:
که در آن را فاکتور لورنتس مینامند و . c سرعت نور در خلأ است و و سرعت v دستگاه ′S در راستای محور xهاست. مختصات y,z تغییری نمیکنند و تنها مختصات x , t تبدیل میشوند. این تبدیلات لورنتس یک گروه تک پارامتر از نگاشتهای خطی تشکیل میدهند که به آن پارامتر تندی (به انگلیسی: rapidity) میگویند. کمیتی که نسبت به تبدیلات لورنتس ناوردا باشد را کمیت نردهای لورنتس مینامند.
چنانچه تبدیلات لورنتس و معکوسشان را برحسب اختلاف مختصاتها بنویسیم به گونهای که مثلاً مختصات یک رویداد (x۱, t۱) and (x′۱, t′۱) باشد، مختصات رویداد دیگر (x۲, t۲) خواهد بود و (x′۲, t′۲) و اختلافها را به صورت زیر تعریف کنیم
به روابط زیر میرسیم
تبدیلات لورنتس که توسط ریاضیدان و فیزیکدان آلمانی هندریک لورنتس با استفاده از روابط هندسی و دو فرض همسانگرد و همگن بودن فضا برای توجیه نظریهٔ اتر به دست آمد اساس نظریهٔ نسبیت خاص میباشد. همسانگرد بودن فضا بدین معناست که خواص آن در تمامی جهات یکسان است. همگن بودن فضا بدین معناست که خواص فضا به نقطهای که شما در آن قرار دارید بستگی ندارد. فرض همسانگرد بودن فضا به ما اجازه میدهد که بتوانیم حرکت ذره را در راستای محور xها بررسی کنیم (یعنی از راستاهای y و z برای خلاصه سازی چشم پوشی کنیم)، فرض همگن بودن فضا تضمین میکند که این معادلات حتماً درجه اول هستند، یعنی تنها توان اول متغیرهای ما میتوانند دخالت داشته باشند. (چون اگر به توان دوم یا درجات بالاتر بستگی داشته باشند اثبات میشود که آنگاه طول یک میله بستگی به نقطهای از فضا که میله در آن قرار گرفتهاست دارد، یعنی مثلاً یک میله که بدون حرکت در ارتفاع ۵ متری قرار دارد با هنگامی که همان میله بدون حرکت در ارتفاع ۳ متری قرار دارد طول متفاوتی دارد و این خلاف شهود ماست)
نکته جالب توجه این است که این معادلات پیش از چاپ مقالهٔ آلبرت انیشتین در رابطه با الکترودینامیک در اجسام متحرک به دست آمده بود اما فرض وجود اتر و فضایی برای انتشار امواج الکترومغناطیس به قدری قوی بود که این تبدیلات به عنوان تلاشی برای اصلاح آن فرضیه عنوان شد. چند سال بعد انیشتین به گونهٔ دیگری با استفاده از دو پنداشتی که در پیش گفته شد به تبدیلات لورنتس رسید! همانگونه که خود انیشتین نیز گفتهاست: «تمامی نتایج نسبیت خاص میتوانند از تبدیلات لورنتس به دست آیند.»
پیامدهای ناشی از تبدیلات لورنتس[ویرایش]
دو اصل موضوع نسبیت خاص به همراه فرضهای دیگری، مانند همگن و همسانگرد بودن فضا، منجر به نتایجی میشوند که همانند خودِ این اصل موضوعها خلاف شهود و تجربههای روزمرهٔ ما هستند. با وجود این، این پیامدها بارها در آزمایشهای گوناگون آزموده شده و مورد تأیید قرار گرفتهاند. امروزه نسبیت خاص کاملاً پذیرفته شدهاست و جزئی از دانش عملی هر فیزیکدانی بهشمار میآید. پیامدهای نسبیت خاص از تبدیلات لورنتس نتیجه میشوند.[۱۹] این تبدیلات و پیرو آن نظریه نسبیت خاص در مواردی که سرعتهای نسبی با سرعت نور قابل مقایسه میشوند نتایجی متفاوت با مکانیک نیوتنی تولید میکنند. سرعت نور بسیار بزرگتر از هرچیزی است که انسانها با آن سر و کار دارند از این رو آثاری که توسط نسبیت خاص پیشبینی شدهاند در آغاز خلاف شهود به نظر میرسند.
نسبی بودن همزمانی[ویرایش]

دو رویداد در مکانهای متفاوت که در چارچوب مرجع یک ناظر لخت همزمان رخ میدهند، ممکن است در چارچوب مرجع یک ناظر لخت دیگر غیر همزمان باشند. (نبود همزمانی مطلق) اگر یک ناظر لخت دو پدیدهٔ آ و ب را همزمان ببیند، ناظر لخت دیگری که با سرعت نسبت به ناظر اول حرکت میکند، بسته به شرایط ممکن است پدیدهٔ آ را زودتر، همزمان، یا دیرتر از پدیدهٔ ب ببیند. همزمانی در نسبیت خاص معنای مطلق و نیوتنی خود را از دست میدهد و پدیدهای نسبی میشود.
از معادله اول تبدیلات لورنتس بر حسب تغییر مختصاتها داریم:
واضح است که دو رویداد که در چارچوب S همزمان هستند (شرط Δt = ۰ صادق است)، الزاماً در دستگاه لخت دیگر ′S همزمان نیستند. تنها در صورتی که این رویدادها در چارچوب S هم مکان باشند (شرط Δx = ۰ صادق باشد) در در دستگاه لخت دیگر ′S نیز همزمان خواهند بود.
انقباض طول[ویرایش]
مقالهٔ اصلی: انقباض طول ابعاد (مانند طول) یک شیء که توسط یک ناظر اندازهگیری میشوند ممکن است از نتایج اندازهگیری یک ناظر دیگر کوچکتر باشند.
مثلاً در نظر بگیرید که میلهای در یک سیستم نامشخص S در حال سکون و در امتداد محور x قرارگرفتهاست. در این دستگاه طول میله اندازهگیری شده Δx است. برای اندازهگیری طول این میله در دستگاه 'S که در آن ساعت در حال حرکت است، فواصل ′x تا نقاط انتهایی میله باید همزمان اندازهگیری شوند. به عبارت دیگر ویژگی اندازهگیری این است که Δt′ = ۰ که میتوان آن را با معادله چهارم ترکیب کرد و رابطه بین Δx و ′Δx را به دست آورد
- برای رویدادهایی که
نتیجه میشود که یک میله که در راستای طول خود در حرکت است، به چشم یک ناظر ساکن، کوتاهتر به نظر میرسد. به زبان ریاضی:
طول میله از دید ناظر 'S است که با سرعت نسبت به چارچوب S که میله در آن ساکن است، حرکت میکند. طول میله در چارچوب سکون S است.
اتساع زمان[ویرایش]
مقالهٔ اصلی:اتساع زمان
بازه زمانی بین دو رویداد از یک ناظر به ناظر دیگر ثابت نیست. بلکه به سرعت نسبی چارچوبهای مرجع ناظرها بستگی دارد.
ساعتی را در نظر بگیرید که در دستگاه غیر ویژه S در حالت سکون قراردارد؛ بنابراین بین دو تیک متوالی ساعت Δx = ۰ خواهد بود. برای اینکه رابطه بین زمانهای اندازهگیری شده بین تیکها در هر دستگاه را بیابیم، میتوانیم از معادله اول استفاده کنیم:
- برای رویدادهایی که
این نشان میدهد که زمان ('Δt) بین دو تیک در دستگاهی که در آن ساعت حرکت میکند('S) طولانیتر از زمان (Δt) بین تیکها که با ساعت چارچوب در حال سکون(S) اندازهگیری شده، خواهد بود. اتساع زمان شماری از پدیدههای فیزیکی را توضیح میدهد. مثلاً میتوان به کاهش نرخ میونهای تولید شده توسط پرتوهای کیهانی در برخورد با جو زمین شاره کرد.[۲۰]
اگر ناظر S یک بازهٔ زمانی را اندازه بگیرد، ناظر 'S همان بازهٔ زمانی را اندازه میگیرد:
یعنی ناظر متحرک آن بازه را طولانیتر میبیند.
ترکیب سرعتها[ویرایش]
افزودن سرعتها چندان ساده نیست. اگر ناظر در S جسمی را در حال حرکت در امتداد محور x با سرعت u اندازهگیری نماید، ناظری که در دستگاه ′S (چارچوب مرجعی که نسبت به S با سرعت v در امتداد محور x حرکت میکند) قرار دارد جسم را در حال حرکت با سرعت 'u اندازهگیری خواهد کرد که با استفاده از تبدیلات لورنتس برای چارچوب ′S داریم
و در چارچوب S:
در نظر داشته باشید که اگر اجسام در چارچوب S در حال حرکت با سرعت نور بودند (u = c) در چارچوب دیگر 'S نیز با سرعت نور حرکت میکردند. همچنین اگر هر دو سرعت u و v نسبت به سرعت نور کوچک باشند به تبدیل شهودی تر گالیلهای برای سرعتها برمی گردیم.
مثالی که معمولاً در این مورد زده میشود مثال قطاری است (چارچوب S در بالا) که با سرعت v نسبت به ریلها (چارچوب S′) حرکت میکند. کودکی درون قطار توپ بیسبالی را به سمت شرق با سرعت u نسبت به قطار پرتاب میکند. در فیزیک کلاسیک ناظری که در حال سکون روی ریلها قرار دارد سرعت توپ بیسبال را
u = u′ + v
اندازهگیری خواهد نمود. در حالیکه در نسبیت خاص این درست نیست بلکه سرعت توپ بیسبال از معادله دوم به دست میآید:
(u = (u′ + v)/(1 + u′v/c²
سایر پیامدها[ویرایش]
چرخش توماس[ویرایش]
جهتگیری یک جسم (یعنی امتداد محورهایش نسبت به محورهای ناظر) برای ناظرین مختلف ممکن است متفاوت باشد. بر خلاف سایر آثار نسبیتی این پدیده در سرعتهای نسبتاً پایین هم مشخص میشود همانطور که در چرخش ذرات متحرک مشاهده میشود.
همارزی جرم و انرژی[ویرایش]
همارزی جرم و انرژی چنانچه سرعت یک جسم از دید یک ناظر به سرعت نور نزدیک گردد، جرم نسبیتی آن افزایش مییابد و از دید چارچوب مرجع ناظر، شتاب گرفتن جسم هر لحظه دشوارتر و دشوارتر به نظر خواهد رسید.
محتوای انرژی جسمی در حال سکون با جرم m برابر با mc² است. پایستگی انرژی ایجاب مینماید که در هر واکنشی کاهش در مجموع جرم ذرات باید با افزایش در انرژی جنبشی ذرات پس از واکنش همراه باشد؛ و متشابها با کاهش انرژی جنبشی، جرم ذرات افزایش مییابد.
افزون بر مقالاتی که در بالا به آنها ارجاع داده شد، انیشتین حداقل چهار مقاله دیگر هم در مورد مباحث اکتشافی در مورد همارزی جرم و انرژی با رابطه E = mc² منتشر نمود.
همارزی جرم و انرژی از نتایج نسبیت خاص است. انرژی و تکانه که در مکانیک نیوتنی مجزا هستند، در نسبیت یک چهار-بردار تشکیل میدهند و بدین ترتیب مولفه زمان (انرژی) و مولفه مکان (تکانه) رابطهای غیر بدیهی با یکدیگر خواهند داشت. برای شیئی که در حال سکون است، جهار-بردار انرژی-تکانه عبارت است از (E, ۰، ۰، ۰): یک مولفه زمان دارد که انرژی است و سه مولفه مکان که صفر هستندبا تغییر چارچوب از طریق تبدیل لورنتز در جهت x با سرعت کوچک v چهار-بردار انرژی-تکانه برابر (E, Ev/c², ۰، ۰) میگردد. تکانه برابر است با انرژی ضربدر سرعت تقسیم بر c². به این ترتیب جرم نیوتنی یک جسم که نسبت تکانه به سرعت است برابر با E/c² خواهد بود.
تکانه و انرژی از ویژگیهای ماده و تابش هستند و غیرممکن است که بتوانیم تنها با استفاده از دو اصل نسبیت خاص بتوانیم نتیجه بگیریم که این دو تشکیل یک چهار-بردار میدهند. زیرا این اصول در مورد ماده و تابش حرفی نمیزنند و تنها از زمان و فضا سخن میگویند؛ بنابراین برای رسیدن به این نتیجه به استدلال فیزیکی بیشتری نیازمندیم. در مقاله سال ۱۹۰۵ خود انیشتین از اصول اضافهای استفاده کرد که در مکانیک نیوتنی هم برای سرعتهای پایین صادق هستند، مثل اینکه در سرعتهای پایین تنها یک کمیت نردهای انرژی و سه بردار تکانه وجود دارند و قانون پایستگی انرژی و تکانه دقیقاً در نسبیت صادق است. علاوه بر این او فرض نمود که انرژی نور نیز مانند بسامدش با همان فاکتور انتقال دوپلر تغییر میکند که قبلاً درستی آن را با استفاده از معادلات ماکسول نشان داده بود.[۱] نخستین مقاله انیشتین در این موضوع، مقاله "آیا لختی یک جسم به محتوای انرژی اش وابسته است؟" بود که در سال ۱۹۰۵ منتشر گردید.[۲۱] گرچه بحثهای انیشتین در این مقاله تقریباً مورد پذیرش همگانی فیزیکدانان قرار گرفتهاست، اما نویسندگان بسیاری نیز در طول سالها پیشنهاد دادهاند که ممکن است این بحثها نادرست باشند.[۲۲] سایر نویسندگان نیز بر این باورند که چون این بحثها بر پایه فرضهای ضمنی بنا شدهاند، بینتیجهاند.[۲۳]
انیشتین وجود اختلاف نظر در مورد نتیجه گیریهایش را در مقالهای در مورد نسبیت خاص در سال ۱۹۰۷ پذیرفته بود. در این مقاله او عنوان میکند که تکیه بر معادلات ماکسول برای بحث اکتشافی جرم انرژی مشکل زاست. بحث او در مقاله سال ۱۹۰۵ میتواند در مورد تابش هر ذره بدون جرمی برقرار باشد اما معادلات ماکسول بهطور ضمنی مورد استفاده قرار گرفتهاند تا مشخص شود که تابش نور میتواند تنها با انجام کار صورت گیرد. برای تابش امواج الکترومغناطیس تنها چیزی که باید انجام شود تکان دادن یک ذره باردار است و این همان انجام کار است و در نتیجه تابش ناشی از انرژی است.[۲۴][۲۵]
یک انسان تا چه اندازه میتواند از زمین دور گردد؟[ویرایش]
از آنجا که هیچکس نمیتواند سریعتر از نور حرکت کند، ممکن است این گونه نتیجهگیری کنیم که اگر عمر مفید انسان را بین ۲۰ تا ۶۰ سال در نظر بگیریم، یک انسان نمیتواند بیشتر از ۴۰ سال نوری از زمین دور شود. اما این نتیجهگیری اشتباه است. به دلیل اتساع زمان یک سفینه خیالی میتواند در طول عمر مفید خلبان آن هزاران سال نوری را بپیماید. اگر سفینه طوری ساخته شود که با شتاب ثابت ۱g حرکت کند، در کمتر از یک سال سرعت آن برای ناظر زمینی تقریباً به سرعت نور میرسد. اتساع زمان عمر فرد را از دید ناظر زمینی افزایش میدهد اما ساعتی که با خلبان سفر میکند چنین تغییری نخواهد داشت. مردم روی زمین زمان بیشتری را نسبت به وی تجربه خواهند کرد یک سفر ۵ ساله وی ½۶ سال در زمین به طول میانجامد و مسافتی برابر ۶ سال نوری را طی خواهد کرد. یک سفر ۲۰ ساله برای وی (۵ سال شتاب گرفتن و ۵ سال کاهش سرعت، هرکدام دوبار) ۳۵۵ سال زمینی به طول میانجامد و در این مدت مسافت ۳۳۱ سال نوری را طی خواهد نمود.[۲۶] یک سفر ۴۰ ساله کامل با شتاب g در روی زمین ۵۸۰۰۰ سال به طول میانجامد و ۵۵۰۰۰ سال نوری را پوشش میدهد. یک سفر ۴۰ ساله با شتاب ۱٫۱g به مدت ۱۴۸۰۰۰ سال زمینی به طول میانجامد و مسافتی برابر ۱۴۰۰۰۰ سال نوری را پوشش خواهد داد که قابل مقایسه با قطر کهکشان راه شیری است. دلیل اینکه میونی که نزدیک به سرعت نور حرکت میکند مسافتی بیشتر از c ضربدر نیمهعمر آن طی میکند نیز همین پدیده اتساع زمان است.[۲۷]
علیت و ممنوعیت حرکت سریعتر از نور[ویرایش]
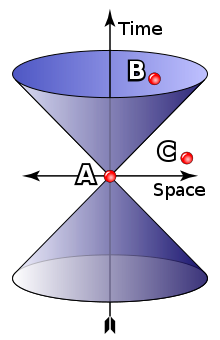
در نمودار شکل مخروط نور، بازه AB یک 'زمان واره' است؛ یعنی چارچوب مرجعی وجود دارد که در آن A و B در یک نقطه مکانی از فضا رخ میدهند و تنها از طریق رخ دادن در زمانهای مختلف از هم جدا میگردند. اگر در آن چارچوب A پیش از B رخ دهد در تمام چارچوبها A پیش از B رخ خواهد داد. به صورت فرضی، ماده (یا اطلاعات) میتواند از A به B حرکت کند پس میتواند رابطه علیتی بین A و B وجود داشته باشد. (A علت و B معلول)
بازه AC در همان شکل یک 'فضاواره' است؛ یعنی چارچوب مرجعی وجود دارد که در آن A و C در یک زمان رخ میدهندو تنها از نظر مکان از هم جدا هستند. در برخی چارچوبها A پیش از C رخ میدهد و در برخی A پس از C رخ میدهد. اگر امکان این بود که رابطه علیتی بین A و C به وجود آید، با پارادوکسهای علیت برخورد میکردیم. مثلاً اگر A علت باشد و C معلول، چارچوبهای مرجعی وجود خواهند داشت که در آنها معلول از علت از نظر زمانی پیشی میگیرد. اگر چه این به خودی خود پارادوکسی را پدیدنمیآورد، اما میتوان نشان داد[۲۸][۲۹] که سیگنالهایی که سریعتر از نور فرستاده شوند میتوانند به گذشته فرد برگردند. اگر فرد سیگنال را تنها در صورتی بفرستد که هیچ سیگنالی در گذشته دریافت نکرده باشد به یک پارادوکس علیتی میرسیم.
بنابراین برای حفظ علیت، یکی از پیامدهای نسبیت خاص این است که هیچ سیگنال اطلاعاتی یا جسم مادی نمیتواند سریعتر از سرعت نور در خلاء حرکت کند. با این حال برخی «چیزها» میتوانند سریعتر از نور حرکت کنند. مثلاً مکانی که پرتو یک نورافکن به پایین ابرها برخورد میکند وقتی که نورافکن سریع میگردد میتواند سریعتر از نور حرکت کند.[۳۰]
حتی بدون در نظر گرفتن علیت هم دلایل دیگری نیز برای اینکه چرا در نسبیت خاص سرعتهای بیشتر از نور ممنوع است وجود دارد. مثلاً اگر نیروی ثابتی برای مدت نامحدودی به جسمی وارد شود، اگر از F = dp/dt انتگرال بگیریم، تکانهای به دست میآوریم که بدون مرز رشد میکند. دلیل این امر این است که وقتی به c میل میکند، به بینهایت میل خواهد کرد. از دید ناظری که در حرکت شتابدار نیست، به نظر خواهد رسید که لختی جسم در حال افزایش است و از این رو همان نیرو شتاب کمتری ایجاد مینماید. این رفتار در شتابدهندههای ذرات مشاهده شدهاست.
گونتر نیمتز و پتریسا اکل در مطالعات تجربی و نظری در مورد تونلزنی کوانتومی ادعا نمودند که سیگنالها ممکن است تحت شرایط خاصی سریعتر از نور حرکت کنند.[۳۱][۳۲][۳۳][۳۴] مشاهده شد که سیگنالهای دیجیتال فیبری با سرعتی در حدود پنج برابر سرعت نور و یک الکترون در تونلی با زمان صفر اطلاعات یونیزه شدن را منتقل نمود به گونهای که فوتونها، فونونها و الکترونها زمان صفر را در مانع تونل زنی گذراندند. بنا بر نیمتز و اکل، این فرایند تنها علیت انیشتین و نسبیت خاص را نقض میکند و علیت پایهای را نقض نمیکند: انتشار با سرعت بیشتر از نور باعث سفر در زمان نمیشود.[۳۵][۳۶] ادعای نیمتز توسط بسیاری از دانشمندان رد یا مورد بحث قرارگرفتهاست.[۳۷][۳۸][۳۹][۴۰]
هندسه فضازمان[ویرایش]
مقایسه بین فضای تخت اقلیدسی و فضای مینکوفسکی[ویرایش]

نسبیت خاص از یک فضای مینکوفسکی تخت چهاربعدی - مثالی از یک فضازمان - استفاده میکند. فضای مینکوفسکی بسیار به فضای اقلیدسی سه بعدی استاندارد شبیه است اما در مورد زمان یک تفاوت اساسی با آن دارد.
در فضای سه بعدی دیفرانسیل فاصله (عنصر خط) ds در رابطه زیر تعریف میشود
که در آن (dx = (dx۱, dx۲, dx۳ دیفرانسیلهای سه بعد فضایی هستند. در هندسه مینکوفسکی یک بعد اضافه با مختصات x۰ دارد که از زمان ناشی میشود، به گونهای که دیفرانسیل فاصله در رابطه زیر صدق کند
که در آن (dx = (dx۰, dx۱, dx۲, dx۳ دیفرانسیلهای چهار بعد فضازمان هستند. این موضوع بینش نظری عمیقی دربردارد: نسبیت خاص به سادگی یک تقارن چرخشی از فضازمان ماست که قابل مقایسه با تقارن چرخشی در فضای اقلیدسی است.[۴۲] همانطور که فضای اقلیدسی از متریک اقلیدسی استفاده میکند، فضازمان نیز از یک متریک مینکوفسکی استفاده میکند. اساساً میتوان نسبیت خاص را ناوردایی هر بازه فضازمان (که در واقع فاصله چهاربعدی بین دو رویداد در فضازمان است) از دید ناظری در هر چارچوب مرجع لخت دلخواه تعریف کرد. تمام معادلات و تأثیرات نسبیت خاص را میتوان از تقارن چرخشی (گروه پوانکاره) فضازمان مینکوفسکی نتیجه گرفت.
شکل واقعی ds به متریک و مختصات x۰ انتخاب شده بستگی دارد. برای اینکه مختصات را شبیه مختصات فضا بکنیم میتوان آن را به عنوان یک عدد موهومی در نظر گرفت: x۰ = ict. میستر، تورن و ویلر در کتاب «گرانش» (۱۹۷۱، §۲٫۳) خود چنین مینویسند که سرانجام درک ژرف تری از هر دو نظریه نسبیت عام و خاص از طریق متریک مینکوفسکی وبا در نظرگرفتن x۰ = ct به جای یک متریک اقلیدسی نقاب زده با مقدار ict به عنوان مختصات زمان، حاصل خواهد شد.
فضازمان سه بعدی[ویرایش]


اگر یکی از ابعاد فضایی را کاهش دهیم تا بتوانیم فیزیک را فضای سه بعدی نمایش دهیم
خواهیم دید که ژئودزیکهای پوچ در امتداد یک مخروط دو تایی (در شکل سمت راست) به معادله زیر قرارمیگیرند
ویا به سادگی
که معادله یک دایره به شعاع c dt است.
فضازمان چهار بعدی[ویرایش]
اگر آن را به سه بعد فضایی افزایش دهیم، ژئودزیکهای پوچ مخروطهای چهاربعدی هستند.
بنابراین
این مخروط دوتایی پوچ «خط دید» را در نقطهای از فضا مشخص میکند، به این معنی که وقتی به ستارگان نگاه میکنیم و میگوییم «نوری که از ستاره به من میرسد X سال عمر دارد»، در واقع ما در امتداد این خط دید را نگاه میکنیم:یک ژئودزیک پوچ. ما به رویدادی در فاصله و در یک زمان d/c در گذشته مینگریم. به همین دلیل مخروط دوتایی پوچ «مخروط نور» نیز نامیده میشود.
مخروط در ناحیه t− اطلاعاتی است که نقطه دریافت میکند و مخروط ناحیه t+ اطلاعاتی است که نقطه میفرستد.
فضای مینکوفسکی را میتوان با استفاده از نمودارهای مینکوفسکی نمایش داد که در فهمیدن بسیاری از آزمایشهای فکری در نسبیت خاص نیز کارساز هستند.
فیزیک در فضازمان[ویرایش]
معادلات نسبیت خاص را میتوان به شکل هم وردای آشکار(به انگلیسی: Manifestly Covariant) نوشت (که در آن همه عبارتها تنسور هستند). موقعیت یک رویداد در فضازمان را توسط یک چهار-بردار پادوَردا (به انگلیسی: Contravariant four vectr) با مؤلفههای
نمایش میدهند. ما x۰ = ct را تعریف میکنیم تا مختصات زمانهمان بعد فاصلهای را داشته باشد که سایر ابعاد فضایی دارند تا بدین وسیله برخورد یکسانی با فضا و زمان داشته باشیم.[۴۳][۴۴][۴۵] بالانویسها در این بخش نمایشگر اندیسهای پادورداها هستند و نه توان؛ مگر در مواردی که مربع یک عبارت را مشخص مینمایند. زیرنویسها نمایشگر اندیسهای همورداها هستند که مقادیری از ۰ تا ۳ میگیرند، مانند چهار-گرادیان میدان نردهای φ:
تبدیلات کمیتهای فیزیکی بین چارچوبهای مرجع[ویرایش]
تبدیلات مختصات بین چارچوبهای مرجع لخت توسط تنسور تبدیلات لورنتس Λ به دست میآید. برای مورد خاص حرکت در امتداد محور x:
که به سادگی ماتریس یک بالابردن (مانند چرخش) بین مختصاتهای x و ct است که در آن 'μ ردیف و ν ستون را نشان میدهند و
تبدیل یک چهار-بردار از یک چارچوب لخت به دیگری (برای سادگی انتقالها را نادیده میگیریم) با تبدیلات لورنتس به دست میآید:
در جاییکه یک جمع زدن ضمنی 'μ و 'ν از ۰ تا ۳ نیز موجود باشد. تبدیل معکوس به صورت زیر خواهد بود:
که در آن ماتریس دوجانبه است.
در ورد تبدیلات لورنتس بالا در راستای x:
به صورت عمومی تر بیشتر کمیتهای فیزیکی به بهترین شکل توسط (مولفههای) تنسورها توصیف میشوند؛ بنابراین برای تبدیل از یک چارچوب به دیگری از قانون مشهور تبدیل تنسور استفاده میکنیم.[۴۶]
که ماتریس معکوس است. تمام تنسورها با همین قانون تبدیل میشوند.
متریک[ویرایش]
از آنجا که فضازمان ماهیتی چهاربعدی دارد، متریک مینکوفسکی مؤلفههایی دارد که میتوان آنها را در یک ماتریس ۴ × ۴ نمایش داد.
که با معکوس خود برابر است،
گروه پوانکاره کلیترین گروه تبدیلات است که متریک مینکوفسکی را حفظ میکند.
واین تقارن فیزیکی سنگ بنای نسبیت خاص است.
ناوردایی[ویرایش]
مجذور طول دیفرانسیل چهار-بردار موقعیت که به صورت زیر به دست میآید،
یک ناوردا است. ناوردا بودن به این معناست که مقدار آن در تمام چارچوبها یکسان است، زیرا یک کمیت نردهای (تنسور با مرتبه صفر) است و از این رو در تبدیلات بدیهی اش عبارت Λ ظاهر نمیشود. توجه کنید که هرگاه عنصر خط، dx²، منفی باشد،
دیفرانسیل زمان ویژه است و اگر dx² مثبت باشد، √(dx²) دیفرانسیل فاصله ویژه خواهد بود.
سرعت و شتاب در فضای چهاربعدی[ویرایش]
در نظر گرفتن کمیتهای فیزیکی به عنوان تنسور قوانین تبدیلشان را نیز سادهتر میسازد. چهار-سرعت Uμ به گونه زیر به دست میآید
با در دست داشتن این رابطه میتوان قانون پیچیده ترکیب سرعتها را به رابطه سادهای برای تبدیل چهار-بردار سرعت یک ذره از یک چارچوب به چارچوب دیگر تبدیل نمود. Uμ یک شکل ناوردا نیز دارد:
بنابراین تمام چهار بردارهای سرعت اندازهای برابر c دارند. این به گونهای بیانگر این واقعیت است که در نسبیت، مختصات در حال سکون وجود ندارد: حداقل شما همیشه در حال حرکت در زمان هستید. چهار-شتاب نیز از رابطه
- محاسبه میشود.
اگر از این معدله به وسیلهٔ τ، دیفرانسیل بگیریم معادله زیر حاصل میشود
بنابراین در نسبیت چهار-بردارهای سرعت و شتاب برهم عمودند.
تکانه در فضای چهاربعدی[ویرایش]
تکانه و انرژی در یک چهار-بردار هم وردا با هم ترکیب میشوند
که در آن m جرم ناوردا است.
اندازه ناوردای چهار-بردار تکانه رابطه انرژی-تکانه را نتیجه میدهد:
این ناوردا یک کمیت نردهای است پس اهمیتی ندارد که در کدام چارچوب محاسبه میشود پس میتوانیم آن را به چارچوبی تبدیل کنیم که در آن تکانه کل برابر صفر است.
میبینیم که انرژی سکون یک ناوردای مستقل است. انرژی سکون را میتوان حتی برای ذرات و دستگاههای در حال حرکت نیز با انتقال آنها به چارچوبی که در آن تکانه صفر است، محاسبه کرد.
انرژی سکون طبق رابطه بنامی که قبلاً به آن اشاره شد، با جرم مرتبط است:
توجه کنید که جرم سامانههایی که در مرکز چارچوب تکانهشان (که در آن تکانه صفر است) اندازهگیری میشوند برابر با انرژی کل سامانه در این چارچوب است. این مقدار ممکن است با مجموع جرم هریک از سیستمها که در چارچوبهای دیگر اندازهگیری شدهاند برابر نباشد.
نیرو در فضای چهاربعدی[ویرایش]
قانون دوم حرکت نیوتن بیان میکند که کل نیروی وارد بریک ذره با نرخ تغییر تکانه اش برابر است. همین شکل از قانون دوم نیوتن در مکانیک نسبیتی نیز صادق است. سه-نیرو ی نسبیتی از رابطه زیر به دست میآید
اگر از جرم نسبیتی استفاده شود:
با استفاده از قانون لایب نیتز :
اگر ذره با سرعت c حرکت نکند، میتوان نیروی سه بعدی از چارچوب مرجع هم حرکت ذره به چارچوب مرجع ناظر تبدیل نمود. در نتیجه چهار-برداری خواهیم داشت که چهار-نیرو نامیده میشود و برابر است با نرخ تغییر چهار-بردار انرژی تکانه نسبت به زمان ویژه. شکل هم وردای چهار نیرو به صورت زیر است:
که در آن τ زمان ویژه است.
درچارچوب سکون جسم، مؤلفه زمان چهار-نیرو برابر صفر خواهد بود مگر آنکه "جرم ناوردای " جسم در حال تغییر باشد؛ که در آن صورت برابر با منفی نرخ تغییر جرم ضربدر c خواهد بود. بهطور کلی مؤلفههای چهار-نیرو با مؤلفههای سه-نیرو برابر نیستند زیرا سه نیرو به صورت نرخ تغییر تکانه نسبت به مختصات زمان تعریف میشود(dp/dt)، در حالیکه چهار-نیرو را نرخ تغییر تکانه نسبت به زمان ویژه تعریف میکنیم(dp/dτ)
مکانیک کوانتومی نسبیتی[ویرایش]
ترکیب و یکپارچه سازی نسبیت خاص با مکانیک کوانتومی برای ایجاد مکانیک کوانتومی نسبیتی یکی از مسئلههای حل نشده فیزیک است. گرانش کوانتومی و نظریه همهچیز شاخههای فعال مورد پژوهش هستند.
در سال ۱۹۲۸ پل دیراک، یک معادله موج نسبیتی ارائه داد که امروزه به نام وی معادله دیراک خوانده میشود[۴۷] و کاملاً با نسبیت خاص و نسخه نهایی نظریه کوانتومی سازگاری داشت. این نظریه نه تنها تکانه زاویهای ذاتی الکترون (اسپین) را توضیح میداد بلکه به پیشبینی وجود پادذره الکترون (پوزیترون) انجامید.[۴۷][۴۸] ساختار ریز را تنها با نسبیت خاص میتوان بهطور کامل توضیح داد. در مکانیک کوانتومی غیر نسبیتی، اسپین قابل توضیح نیست.
از سوی دیگر وجود پادذرهها به این نتیجه میانجامد که یکپارچه سازی خام نسبیت و مکانیک کوانتوم امکانپذیر نیست در عوض یک نظریه میدانهای کوانتومی مورد نیاز است که در آن ذرات میتوانند در تمام فضا به وجود آیند و نابود شوند. (مانند الکترودینامیک کوانتومی یا کرومودینامیک کوانتومی). این عناصر با مدل استاندارد فیزیک ذرات آمیخته میشوند.
وضعیت نظریه[ویرایش]
نسبیت خاص در فضای مینکوفسکی تنها هنگامی دقیق است که قدرمطلق پتانسیل گرانشی در ناحیه مورد نظر بسیار کمتر از c۲ باشد.[۴۹] در میدان گرانشی قوی باید از نسبیت عام یاری جست. نسبیت عام در محدوده میدانهای ضعیف به نسبیت خاص تبدیل میگردد. در مقیاسهای خیلی کوچک، مثلاً در طول پلانک و کمتر باید آثار کوانتومی را در نظر گرفت که گرانش کوانتومی را نتیجه میدهد. اما در مقیاسهای ماکروسکوپیک و در غیاب میدانهای گرانشی قوی، نسبیت خاص در آزمایشهای تجربی دقت بالایی (۱۰−۲۰) را به نمایش میگذارد[۵۰] و از این رو از سوی جامعه فیزیک مورد پذیرش قرارگرفتهاست.
مکانیک نیوتنی از نظر ریاضی در سرعتهای کوچک از نسبیت خاص پیروی میکند و از این رو مکانیک نیوتنی را میتوان مکانیک اجسام متحرک با سرعت پایین دانست. چندین آزمایش که پیش از مقاله ۱۹۰۵ انیشتین انجام شدند اکنون به عنوان گواهی بر درستی این نظریه بهشمار میروند. از میان این آزمایشها، این آگاهی در دسترس است که انیشتین پیش از ۱۹۰۵ از آزمایش فیزو باخبر بود.[۵۱] برخی از تاریخ نگاران بر این باورند که انیشتین حداقل تا سال ۱۸۹۹ از آزمایش مایکلسون-مورلی نیز آگاهی داشتهاست.[۱۸]
- • آزمایش فیزو (۱۸۵۱ و تکرار آن توسط مایکلسون و مورلی در سال ۱۸۸۶) سرعت نور را در رسانه در حال حرکت اندازهگیری کرد که نتایج آن با افزودن سرعتهای هم خط در نسبیت، همخوانی دارند.
- • آزمایش بنام مایکلسون-مورلی (۱۸۸۱و۱۸۸۷) پشتوانهای برای این اصل بود که سرعت مرجع مطلقی وجود ندارد.
شتابدهندههای ذرات، به ذرات شتاب میدهند و ویژگیهای ذرات را در سرعتهای بالا نزدیک به سرعت نور اندازه میگیرند. در این سرعتها رفتار ذرات کاملاً با نظریه نسبیت همخوانی دارد و با مکانیک نیوتنی ناسازگار است. اگر این ماشینها بر اساس اصول نسبیتی مهندسی نشده بودند، نمیتوانستند کار کنند. افزون بر این شمار زیادی از آزمایشهای جدید نیز برای آزمودن نظریه نسبیت انجام شدهاند. از این دسته آزمایشها میتوان به موارد زیر اشاره نمود:
- • آزمونهای انرژی و تکانه نسبیتی - آزمودن حد سرعت ذرات
- • آزمایش آیوس-استیلول - آزمودن اثر دوپلر نسبیتی و اتساع زمان
- • اتساع زمان ذرات متحرک - آثار نسبیتی در نیمه عمر ذرات با سرعت بالا
- • آزمایش کندی-تورندایک - اتساع زمان بر پایه تبدیلات لورنتس
- • آزمایش هیوز-درور - آزمودن همسانگردی جرم و فضا
- • جستجوهای جدید برای نقض لورنتس - آزمونهای جدید گوناگون
انتقادات علیه نسبیت خاص اکثراً در سالهای نخستین انتشار نظریه در دهه ۱۹۰۰ وارد شدند و این نظریه را از دیدگاههای علمی، شبه علمی، فلسفی و ایدئولوژیک مورد انتقاد قرار دادند. با وجود اینکه برخی از این انتقادات از پشتیبانی دانشمندان بنام نیز برخوردار شدند، نظریه نسبیت امروزه به عنوان یک نظریه قائم بالذات و سازگار با شواهد تجربی شناخته میشود و پایه برخی از نظریات موفق از جمله الکترودینامیک کوانتومی میباشد.
جستارهای وابسته[ویرایش]
| در ویکیانبار پروندههایی دربارهٔ نسبیت خاص موجود است. |
پیوند به بیرون[ویرایش]
آثار اصلی[ویرایش]
- Zur Elektrodynamik bewegter Körper مقاله اصلی انیشتین به زبان آلمانی، سالنامه فیزیک، برن ۱۹۰۵
- On the Electrodynamics of Moving Bodies ترجمه انگلیسی مطابق آنچه در سال ۱۹۲۳ در کتاب The Principle of Relativity به چاپ رسید.
کلاس درس و جزوههای دانشگاهی[ویرایش]
- دوره فیزیک مدرن: نسبیت خاص (دانشگاه استانفورد) مجوعه کلاسهای درسی لئونارد ساسکیند متشکل از هشت جلسه کلاس در مورد نسبیت خاص
- جزوههای کلاس نسبیت خاص ساسکیند
- جزوههای نسبیت خاص مقدمهای استاندارد برای نسبیت خاص شامل تصاویر و توضیحات و نمودارهای فضازمان از دانشگاه پلی تکنیک ویرجینیا.
- جزوههای نسبیت خاص توسط جی دی کرسر از دانشگاه مک کوئری استرالیا.
نسبیت خاص برای مخاطبین عام (بدون نیاز به دانستن دانش ریاضی)[ویرایش]
- Wikibooks: Special Relativity
- Einstein Light [۲]، مقدمهای غیر تخصصی (فیلم و نمایشهایی که با بسیاری از صفحات حاوی توضیحات مفصل تر برای سطوح مختلف بدو ن استفاده از ریاضیات و با استفاده از آن همراه شده).
- Einstein Online بایگانیشده در ۱ فوریه ۲۰۱۰ توسط Wayback Machine مقدمهای بر نظریه نسبیت، از انستیتوی فیزیک گرانشی ماکس پلانک
- شنیداری: Cain/Gay (2006) - Astronomy Cast. نظریه نسبیت خاص انیشتین
توضیح نظریه نسبیت خاص (با کمک ریاضیات ساده و پیشرفته)[ویرایش]
- مفاهیم بنیادی نوشته گرگ ایگان.
- یادداشتهای هاگ در نسبیت خاص مقدمهای خوب بر نسبیت عام در سطح کارشناسی با استفاده از حساب دیفرانسیل و انتگرال.
- ماشین حساب نسبیت: نسبیت خاص - نتیجهگیری E = mc۲ با استفاده از حساب انتگرال و جبر.
- Motion Mountain, Volume II - مقدمهای پیشرفته بر نسبیت خاص همراه با تأثیرات دیداری آن.
- MathPages - بازتابهایی از نسبیت یک کتاب آنلاین کامل در مورد نسبیت با منبعشناسی بسیار گسترده.
- Relativity مقدمه بر نسبیت خاص در سطح کارشناسی بدون استفاده از حساب دیفرانسیل و انتگرال.
- کتاب الکترونیکی رایگان Relativity: the Special and General Theory در پروژهٔ گوتنبرگ، از آلبرت انیشتین
- فهمیدن نسبیت خاص نظریه نسبیت خاص به صورتی که به آسانی فهمیده میشود.
- An Introduction to the Special Theory of Relativity (۱۹۶۴) نوشته Robert Katz، «مقدمهای که برای دانشجویانی که آشنایی مقدماتی با فیزیک و حساب دیفرانسیل دارند سودمند خواهد بود» (۱۳۰ pp; pdf format).
تصویر سازی[ویرایش]
- نورپردازی نسبیت خاص نرمافزاری که سناریوهای مختلفی را تخت تأثیر نسبیت خاص تصویر سازی میکند.
- نسبیت بیدرنگ دانشگاه ملی استرالیا. ویژگیهای دیداری تجربه شده توسط نسبیت خاص.
- سفر در فضازمان مجموعهای متنوع از تصویر سازیهای پدیدههای نسبیتی از حرکت نسبیتی به سوی سیاهچاله.
- از دید انیشتین دانشگاه ملی استرالیا. توضیح آثار دیداری نسبیتی با فیلم و عکس.
- Warp Special Relativity Simulator برنامهای رایانهای برای نمایش آثار نزدیک شدن به سرعت نور.
- کلیپهای انیمیشن تصویر سازی تبدیلات لورنتس.
- انیمیشنهای فلش تعاملی به تصویر کشیدن چارچوبهای لورنتسی و گالیلهای، پارادوکس قطار و تونل، پارادوکس دوقلوها، انتشار موج، همزمانی ساعتها و غیره.
- نورشناسی نسبیتی در دانشگاه ملی استرالیا
- [۳][پیوند مرده] برنامهای بر پایه openGL که آثار نسبیت خاص را در ظاهر اجسام متحرک نشان میدهد.
منابع[ویرایش]
- ↑ ۱٫۰ ۱٫۱ ۱٫۲ ۱٫۳ آلبرت انیشتین (1905) "Zur Elektrodynamik bewegter Körper بایگانیشده در ۲۹ دسامبر ۲۰۰۹ توسط Wayback Machine", Annalen der Physik 17: 891؛ ترجمه انگلیسی On the Electrodynamics of Moving Bodies توسط جرج بارکر جفری و ویلفرید پرت (۱۹۲۳)؛ یک ترجمه انگلیسی دیگر On the Electrodynamics of Moving Bodies از مق ند ساها (۱۹۲۰).
- ↑ Edwin F. Taylor and John Archibald Wheeler (1992). Spacetime Physics: Introduction to Special Relativity. W. H. Freeman. ISBN 0-7167-2327-1.
- ↑ Wolfgang Rindler (1977). Essential Relativity. Birkhäuser. p. §1,11 p. 7. ISBN 3-540-07970-X.
- ↑ Tom Roberts and Siegmar Schleif (2007). "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. Retrieved 2008-09-17.
- ↑ Albert Einstein (2001). Relativity: The Special and the General Theory (Reprint of 1920 translation by Robert W. Lawson ed.). Routledge. p. 48. ISBN 0-415-25384-5.
- ↑ Richard Phillips Feynman (1998). Six Not-so-easy Pieces: Einstein's relativity, symmetry, and space-time (Reprint of 1995 ed.). Basic Books. p. 68. ISBN 0-201-32842-9.[پیوند مرده]
- ↑ Albert Einstein, Relativity — The Special and General Theory, chapter 18
- ↑ چارلز میسنر، کیپ تورن & جان ویلر، Gravitation, pg 172, 6.6 The local coordinate system of an accelerated observer, ISBN 0-7167-0344-0
- ↑ ۹٫۰ ۹٫۱ Einstein, Autobiographical Notes, 1949.
- ↑ ۱۰٫۰ ۱۰٫۱ Einstein, "Fundamental Ideas and Methods of the Theory of Relativity", 1920
- ↑ Einstein, A. , Lorentz, H. A. , Minkowski, H. , & Weyl, H. (1952). The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity. Courier Dover Publications. p. 111. ISBN 0-486-60081-5.
{{cite book}}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - ↑ Einstein, On the Relativity Principle and the Conclusions Drawn from It, 1907; "The Principle of Relativity and Its Consequences in Modern Physics", 1910; "The Theory of Relativity", 1911; Manuscript on the Special Theory of Relativity, 1912; Theory of Relativity, 1913; Einstein, Relativity, the Special and General Theory, 1916; The Principle Ideas of the Theory of Relativity, 1916; What Is The Theory of Relativity?, 1919; The Principle of Relativity (Princeton Lectures), 1921; Physics and Reality, 1936; The Theory of Relativity, 1949.
- ↑ Das, A. , The Special Theory of Relativity, A Mathematical Exposition, Springer, 1993.
- ↑ Schutz, J. , Independent Axioms for Minkowski Spacetime, 1997.
- ↑ Yaakov Friedman, Physical Applications of Homogeneous Balls, Progress in Mathematical Physics 40 Birkhäuser, Boston, 2004, pages 1-21.
- ↑ David Morin, Introduction to Classical Mechanics, Cambridge University Press, Cambridge, 2007, chapter 11, Appendix I
- ↑ مایکل پولانی، Personal Knowledge: Towards a Post-Critical Philosophy, 1974, ISBN 0-226-67288-3, footnote page 10-11: انیشتین از طریق دکتر بالزاس و در پاسخ به پرسش پولانی اعلام نمود که "آزمایش میکلسون مورلی هیچ نقشی در پایه ریزی این نظریه نداشتهاست." و "نظریه نسبیت به هیچ وجه برای توجیه نتیجه این آزمایش بوجود نیامد.."[۱]
- ↑ ۱۸٫۰ ۱۸٫۱ Dongen, Jeroen van (2009). "On the role of the Michelson–Morley experiment: Einstein in Chicago" (PDF). Eprint arXiv:0908.1545. 0908: 1545. arXiv:0908.1545. Bibcode:2009arXiv0908.1545V.
- ↑ Resnick, Robert (1968). Introduction to special relativity. Wiley. pp. 62–63.
- ↑ Kleppner, Daniel; Kolenkow, David (1973). An Introduction to Mechanics. pp. 468–70.
- ↑ Does the inertia of a body depend upon its energy content? A. Einstein, Annalen der Physik. 18:639, 1905 (ترجمه انگلیسی از W. Perrett وG.B. Jeffery)
- ↑ Max Jammer (1997). Concepts of Mass in Classical and Modern Physics. Courier Dover Publications. pp. 177–178. ISBN 0-486-29998-8.
- ↑ John J. Stachel (2002). Einstein from B to Z. Springer. p. 221. ISBN 0-8176-4143-2.
- ↑ On the Inertia of Energy Required by the Relativity Principle, A. Einstein, Annalen der Physik 23 (1907): 371-384
- ↑ در نامهای به کارل سیلینگ در سال ۱۹۵۵، انیشتین چنین مینویسد که «من قبلاً فهمیده بودم که نظریه ماکسول ریزساختار تابش را درنظر نگرفتهاست و در نتیجه اعتبار عمومی ندارد».letter to Carl Seelig, 1955.
- ↑ Gibbs, Philip. "The Relativistic Rocket". Archived from the original on 13 October 2015. Retrieved 30 August 2012.
- ↑ http://library.thinkquest.org/C0116043/specialtheorytext.htm بایگانیشده در ۲۱ اکتبر ۲۰۱۲ توسط Wayback Machine Thinkquest org
- ↑ R. C. Tolman, The theory of the Relativity of Motion, (Berkeley 1917), p. 54
- ↑ G. A. Benford, D. L. Book, and W. A. Newcomb, The Tachyonic Antitelephone, Phys. Rev. D 2, 263–265 (1970) article
- ↑ Salmon, Wesley C. (2006). Four Decades of Scientific Explanation. University of Pittsburgh. p. 107. ISBN 0-8229-5926-7., Section 3.7 page 107
- ↑ F. Low and P. Mende, A Note on the Tunneling Time Problem, Ann. Phys. NY, 210, 380-387 (1991)
- ↑ A. Enders and G. Nimtz, On superluminal barrier traversal, J. Phys. I, France 2, 1693-1698 (1992)
- ↑ S. Longhi et al. , Measurement of superluminal optical tunneling times in double-barrier photonic band gaps, Phys.Rev. E, 65, 06610 1-6 (2002)
- ↑ P. Eckle et al. , Attosecond Ionization and Tunneling Delay Time Measurements in Helium, Science, 322, 1525-1529 (2008)
- ↑ G. Nimtz, Do Evanescent Modes Violate Relativistic Causality?, Lect.Notes Phys. 702, 506-531 (2006)
- ↑ G. Nimtz, Tunneling Violates Special Relativity, arXiv:1003.3944v1
- ↑ Herbert Winful (2007-09-18). "Comment on "Macroscopic violation of special relativity" by Nimtz and Stahlhofen". arXiv:0709.2736 [quant-ph].
- ↑ Chris Lee (2007-08-16). "Latest "faster than the speed of light" claims wrong (again)".
- ↑ Winful, Herbert G. (December 2006). "Tunneling time, the Hartman effect, and superluminality: A proposed resolution of an old paradox" (PDF). Physics Reports. 436 (1–2): 1–69. Bibcode:2006PhR...436....1W. doi:10.1016/j.physrep.2006.09.002. Archived from the original (PDF) on 18 December 2011. Retrieved 15 April 2013.
- ↑ تعدادی از مقالات در مقالات در زمینه آزمایشهای تونل زنی سریعتر از نور لیست شدهاند
- ↑ J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. p. 58. ISBN 0-7167-0344-0.
{{cite book}}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - ↑ J.R. Forshaw, A.G. Smith (2009). Dynamics and Relativity. Wiley. p. 247. ISBN 978-0-470-01460-8.
- ↑ Jean-Bernard Zuber & Claude Itzykson, Quantum Field Theory, pg 5 , ISBN 0-07-032071-3
- ↑ Charles W. Misner, Kip S. Thorne & John A. Wheeler,Gravitation, pg 51, ISBN 0-7167-0344-0
- ↑ George Sterman, An Introduction to Quantum Field Theory, pg 4 , ISBN 0-521-31132-2
- ↑ M. Carroll, Sean (2004). Spacetime and Geometry: An Introduction to General Relativity (illustrated ed.). Addison Wesley. p. 22. ISBN 0-8053-8732-3.
- ↑ ۴۷٫۰ ۴۷٫۱ Dirac, P.A.M. (1930). "A Theory of Electrons and Protons". Proc. R. Soc. A126: 360. Bibcode:1930RSPSA.126..360D. doi:10.1098/rspa.1930.0013. JSTOR 95359.
- ↑ C.D. Anderson: The Positive Electron. Phys. Rev. 43, 491-494 (1933)
- ↑ Grøn, Øyvind; Hervik, Sigbjørn (2007). Einstein's general theory of relativity: with modern applications in cosmology. Springer. p. 195. ISBN 0-387-69199-5., Extract of page 195 (with units where c=1)
- ↑ The number of works is vast, see as example:
Sidney Coleman, Sheldon L. Glashow, Cosmic Ray and Neutrino Tests of Special Relativity, Phys. Lett. B405 (1997) 249-252, online
An overview can be found on this page - ↑ Norton, John D., John D. (2004), "Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905", Archive for History of Exact Sciences, 59: 45–105, Bibcode:2004AHES...59...45N, doi:10.1007/s00407-004-0085-6
کتابها[ویرایش]
- Einstein, Albert (1920). Relativity: The Special and General Theory.
- Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1-56731-136-9
- Freund, Jürgen (2008) Special Relativity for Beginners - A Textbook for Undergraduates World Scientific. ISBN 981-277-160-3
- Logunov, Anatoly A. (۲۰۰۵) Henri Poincaré and the Relativity Theory (transl. from Russian by G. Pontocorvo and V. O. Soleviev, edited by V. A. Petrov) Nauka, Moscow.
- چارلز مینسر، کیپ تورن، و جان ویلر (۱۹۷۱) Gravitation. W. H. Freeman & Co. ISBN 0-7167-0334-3
- Post, E.J. , ۱۹۹7 (1962) Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications.
- Wolfgang Rindler (1991). Introduction to Special Relativity (2nd ed.), Oxford University Press. ISBN 978-0-19-853952-0; ISBN 0-19-853952-5
- Harvey R. Brown (2005). Physical relativity: space-time structure from a dynamical perspective, Oxford University Press, ISBN 0-19-927583-1; ISBN 978-0-19-927583-0
- Qadir, Asghar (1989). Relativity: An Introduction to the Special Theory. Singapore: World Scientific Publications. p. 128. ISBN 9971-5-0612-2.
- Silberstein, Ludwik (1914) The Theory of Relativity.
- Lawrence Sklar (1977). Space, Time and Spacetime. University of California Press. ISBN 0-520-03174-1.
- Lawrence Sklar (1992). Philosophy of Physics. Westview Press. ISBN 0-8133-0625-6.
- Richard A. Mould, Basic Relativity, Springer, 1994, ISBN 0-387-94188-6
- Taylor, Edwin, and John Archibald Wheeler (1992) Spacetime Physics (2nd ed.). W.H. Freeman & Co. ISBN 0-7167-2327-1
- Tipler, Paul, and Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman & Co. ISBN 0-7167-4345-0
- کلیفورد ام. ویل، آیا اینشتین درست میگفت؟: آزمون نسبیت عام، ترجمهٔ احمد شریعتی، انشارات وزارت فرهنگ و ارشاد اسلامی، ۱۳۸۳.
- دانیل کلپنر و رابرت کلنکو، آشنایی با مکانیک، ترجمهٔ هوشنگ سپهری، محمد علی مقیمی، ولیالله ناصری، چاپ چهارم، مرکز نشر دانشگاهی، ۱۳۸۴.
مقالات ژورنال[ویرایش]
- Alvager, et al. ; Farley, F. J. M.; Kjellman, J.; Wallin, L. (1964). "Test of the Second Postulate of Special Relativity in the GeV region". Physics Letters. ۱۲ (۳): 260. Bibcode:1964PhL....12..260A. doi:10.1016/0031-9163(64)91095-9.
- Darrigol, Olivier (2004). "The Mystery of the Poincaré-Einstein Connection". Isis. ۹۵ (۴): ۶۱۴–۲۶. doi:10.1086/430652. PMID 16011297.
- Wolf, Peter; Petit, Gerard (1997). "Satellite test of Special Relativity using the Global Positioning System". Physical Review A. ۵۶ (۶): ۴۴۰۵–۰۹. Bibcode:1997PhRvA..56.4405W. doi:10.1103/PhysRevA.56.4405.






























































