ماشین بردار پشتیبانی
ماشین بردار پشتیبانی (Support vector machines - SVMs) یکی از روشهای یادگیری بانظارت[۱] است که از آن برای طبقهبندی[۲] و رگرسیون[۳] استفاده میکنند. مبنای کاری دستهبندی کنندهٔ SVM دستهبندی خطی دادهها است و در تقسیم خطی دادهها سعی میکنیم ابرصفحه ای را انتخاب کنیم که حاشیه اطمینان بیشتری داشته باشد. حل معادله پیدا کردن خط بهینه برای دادهها به وسیله روشهای برنامه سازی غیرخطی که روشهای شناخته شدهای در حل مسائل محدودیتدار هستند صورت میگیرد. قبل از تقسیمِ خطی برای اینکه ماشین بتواند دادههای با پیچیدگی بالا را دستهبندی کند دادهها را به وسیلهٔ تابعِ phi به فضای با ابعاد خیلی بالاتر[۴] میبریم. برای اینکه بتوانیم مسئله ابعاد خیلی بالا را با استفاده از این روشها حل کنیم از قضیه دوگانی لاگرانژ[۵] برای تبدیلِ مسئلهٔ مینیممسازی مورد نظر به فرم دوگانی آن که در آن به جای تابع پیچیدهٔ phi که ما را به فضایی با ابعاد بالا میبرد، تابعِ سادهتری به نامِ تابع هسته (کرنل) که ضرب برداری تابع phi است ظاهر میشود استفاده میکنیم. از توابع هسته مختلفی از جمله هستههای نمایی، چندجملهای و سیگموید میتوان استفاده نمود. یکی از معروفترین خودآموزها مربوط به[۶] است.
کاربردهای SVM[ویرایش]
الگوریتم SVM، جزو الگوریتمهای تشخیص الگو دستهبندی میشود. از الگوریتم SVM، در هر جایی که نیاز به تشخیص الگو یا دستهبندی اشیا در کلاسهای خاص باشد میتوان استفاده کرد. در ادامه به کاربردهای این الگوریتم به صورت موردی اشاره میشود:
سیستم آنالیز ریسک، کنترل هواپیما بدون خلبان، ردیابی انحراف هواپیما، شبیهسازی مسیر، سیستم راهنمایی اتوماتیک اتومبیل، سیستمهای بازرسی کیفیت، آنالیز کیفیت جوشکاری، پیشبینی کیفیت، آنالیز کیفیت کامپیوتر، آنالیز عملیاتهای آسیاب، آنالیز طراحی محصول شیمیایی، آنالیز نگهداری ماشین، پیشنهاد پروژه، مدیریت و برنامهریزی، کنترل سیستم فرایند شیمیایی و دینامیکی، طراحی اعضای مصنوعی، بهینهسازی زمان پیوند اعضا، کاهش هزینه بیمارستان، بهبود کیفیت بیمارستان، آزمایش اتاق اورژانس، اکتشاف روغن و گاز، کنترل مسیر در دستگاههای خودکار، ربات، جراثقال، سیستمهای بصری، تشخیص صدا، اختصار سخن، کلاسه بندی صوتی، آنالیز بازار، سیستمهای مشاورهای محاسبه هزینه موجودی، اختصار اطلاعات و تصاویر، خدمات اطلاعاتی اتوماتیک، مترجم لحظهای زبان، سیستمهای پردازش وجه مشتری، سیستمهای تشخیص ترمز کامیون، زمانبندی وسیله نقلیه، سیستمهای مسیریابی، کلاسه بندی نمودارهای مشتری/بازار، تشخیص دارو، بازبینی امضا، تخمین ریسک وام، شناسایی طیفی، ارزیابی سرمایه، کلاسه بندی انواع سلولها، میکروبها و نمونهها، پیشبینی فروشهای آینده، پیشبینی نیازهای محصول، پیشبینی وضعیت بازار، پیشبینی شاخصهای اقتصادی، پیشبینی ملزومات انرژی، پیشبینی واکنشهای دارویی، پیشبینی بازتاب محصولات شیمیایی، پیشبینی هوا، پیشبینی محصول، پیشبینی ریسک محیطی، پیشبینی جداول داوری، مدل کردن کنترل فرایند، آنالیز فعالیت گارانتی، بازرسی اسناد، تشخیص هدف، تشخیص چهره، انواع جدید سنسورها، دستگاه کاشف زیر دریایی به وسیلهٔ امواج صوتی، رادار، پردازش سیگنالهای تصویری شامل مقایسه اطلاعات، پیگیری هدف، هدایت جنگافزارها، تعیین قیمت وضعیت فعلی، جلوگیری از پارازیت، شناسایی تصویر /سیگنال، چیدمان یک مدار کامل، بینایی ماشین، مدل کردن غیر خطی، ترکیب صدا، کنترل فرایند ساخت، آنالیز مالی، پیشبینی فرایندهای تولید، ارزیابی بهکارگیری یک سیاست، بهینهسازی محصول، تشخیص ماشین و فرایند، مدل کردن کنترل سیستمها، مدل کردن ساختارهای شیمیایی، مدل کردن سیستمهای دینامیکی، مدل کردن سیگنال تراکم، مدل کردن قالبسازی پلاستیکی، مدیریت قراردادهای سهام، مدیریت وجوه بیمه، دیریت سهام، تصویب چک بانکی، اکتشاف تقلب در کارت اعتباری، ثبت نسیه، بازبینی امضا از چکها، پیشبینی ارزش نسیه، مدیریت ریسک رهن، تشخیص حروف و اعداد، تشخیص بیماری و…
تاریخچه[ویرایش]
الگوریتم SVM اولیه سال ۱۹۶۴ توسط ولادیمیر وپنیک و الکسی چرونینکیس در مؤسسه علوم کنترل آکادمی علوم روسیه ابداع شد. در سال ۱۹۹۲بوزر، ایزابل گایون و وپنیک با مطرح کردن هسته (کرنل) و افزودن آن به SVM راهی برای کلاس بندی غیرخطی ارائه کردند[۷] و در سال ۱۹۹۵ کورینا کورتس و وپنیک soft-margin SVM را معرفی کردند.[۸]
ماشین بردار پشتیبان خطی[ویرایش]
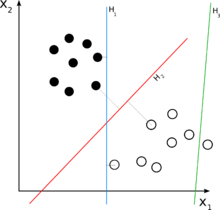

ما مجموعه دادههای آزمایش شامل n عضو (نقطه) را در اختیار داریم که به صورت زیر تعریف میشود:
جایی که مقدار برابر یا و هر یک بردار حقیقی -بعدی است. هدف پیدا کردن ابرصفحه جداکننده با بیشترین فاصله از نقاط حاشیهای است که نقاط با را از نقاط با جدا کند. هر ابر صفحه میتواند به صورت مجموعهای از نقاط که شرط زیر را ارضا میکنند نوشته شود:
جایی که. علامت ضرب است. بردار نرمال است، که به ابرصفحه عمود است. ما میخواهیم و را طوری انتخاب کنیم که بیشترین فاصله بین ابر صفحههای موازی که دادهها را از هم جدا میکنند، ایجاد شود. این ابرصفحهها با استفاده از رابطه زیر توصیف میشوند.
هر داده ایی بالای ابرصفحه جداکننده با لیبل ۱ مشخص میشود:
و هر داده ایی پایین ابرصفحه جدا کننده با لیبل ۱-:
Hard-margin (حاشیه سخت)[ویرایش]
اگر دادههای آموزشی جدایی پذیر خطی باشند، ما میتوانیم دو ابر صفحه در حاشیه نقاط بهطوریکه هیچ نقطه مشترکی نداشته باشند، در نظر بگیریم و سپس سعی کنیم، فاصله آنها را، حداکثر کنیم. با استفاده از هندسه، فاصله این دو صفحه است؛ بنابراین ما باید را مینیمم کنیم. برای اینکه از ورود نقاط به حاشیه جلوگیری کنیم، شرایط زیر را اضافه میکنیم: برای هر میتواند به صورت زیر نوشته شود:
با کنار هم قرار دادن این دو یک مسئله بهینهسازی به دست میآید:
فرم اولیه[ویرایش]
مسئله بهینهسازی مشاهده شده در قسمت قبل، مسئله سختی، برای حل کردن است، زیرا به وابسته است (نرم یا اندازه طول بردار). خوشبختانه میتوانیم، بدون تغییر در مسئله را با جانشین کنیم (عبارت ½ برای آسودگی در محاسبات ریاضی آمده). این یک مسئله بهینهسازی (OP) برنامهریزی غیرخطی (QP) است. بهطور واضح تر:
میتوان عبارت قبل را با استفاده از ضرایب نامنفی لاگرانژ به صورت زیر نوشت که در آن ضرایب لاگرانژ هستند:
اما فرمول فوق اشتباه است. فرض کنید ما بتوانیم خانوادهای از ابر صفحات که نقاط را تقسیم میکنند پیدا کنیم. پس همه . بنابراین ما میتوانیم مینیمم را با فرستادن همه به پیدا کنیم. با این حال شرط پیش گفته میتواند به صورت پایین بیان شود:
ما به دنبال نقاط saddle میگردیم. حالا میتوان این مسئله را به کمک برنامهریزی غیرخطی استاندارد حل کرد. جواب میتواند به صورت ترکیب خطی از بردارهای آموزشی بیان شود:
تنها چند بزرگتر از صفر خواهد بود. متناظر، دقیقاً همان بردار پشتیبان خواهد بود و به شرط را ارضا خواهد کرد. از این میتوان نتیجه گرفت که بردارهای پشتیبان شرط زیر را نیز ارضا میکنند:
که اجازه میدهد مقدار b تعریف شود. در عمل الگوریتم مقاوم تر خواهد بود اگر از تمام بردار پشتیبان میانگین گرفته شود:
فرم دوگان[ویرایش]
استفاده از این واقعیت که و جانشینی میتوان نشان داد که دوگان SVM به مسئله بهینهسازی زیر ساده میشود:
در اینجا هسته (کرنل) به صورت تعریف میشود. عبارت تشکیل یک دوگان برای بردار وزنها مجموعه آموزشی میدهد:
حاشیه نرم (Soft-margin)[ویرایش]
استفاده از روش سخت میتواند در مواردی محدودیتهایی ایجاد کند که یکی از آنها وابستگی شدید جداکننده به دادههای مرزی است و اگر دادهای در مرز ابرصفحه جداکننده قرار گیرد منجر به کاهش margin (حاشیه) و تغییر شدید در ابرصفحه مورد نظر میشود ین نکته حائز اهمیت است که دادههای ما در واقعیت در اکثر موارد مقداری Noise دارند و بنابراین مشکل بالا میتواند اثر نامطلوبی روی مرز تصمیمگیری ما داشته باشد؛ بنابراین مدل Hard-margin به شدت قابلیت بیشبرازش شدن دارند.

به منظور جلوگیری و حل این مشکل، حاشیه نرم (soft-margin) ارائه شد که اجازه میدهد در فرایند آموزش مدل، تعدادی از دادهها به درستی کلاسبندی نشده و حاشیه تعیین شده را نقض کنند تا درنتیجه از بیشبرازش شدن در هنگام تست جلوگیری شود. به عبارتی با این کار نوعی عمومیت (Generalization) به مدل داده میشود تا بر روی دادههای تست عملکرد بهتری داشته باشد. باید گفت، به به منظور ممانعت از کاهش دقت مدل (Model Accuracy)، اینکار با افزودن یک سری پارامتر و به صورت کنترل شده انجام میشود؛ به این متغیرهای کمکی یا لنگی (Slack) گفته میشود و با نماد ξ نمایش داده میشوند. این متغیرها برای هر داده، میزان تخطی آن از مرز تعیین شده را مشخص میکند؛ اگر مقدار آنها صفر باشد به این معنی است که داده در سمت درستی از مرز قرار گرفته و اگر مقدار آنها بزرکتر از صفر باشد، بدان معناست که مقدار خطا را نشان میدهند.
در ادامه همه ξها جمع زده میشوند و در ضریب C ضرب میشوند و به عبارتی که در Hard-margin داشتیم اضافه میشوند تا عبارت خطای جدید به دست آید، که برای رسیدن به هدف خود میبایست عبارت زیر را کمینه کنیم:
ماشینهای بردار پشتیبان غیرخطی[ویرایش]
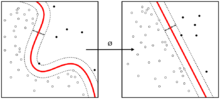
ابرصفحه جداکننده بهینه اولین بار توسط وپنیک در سال ۱۹۶۳ ارائه شد که یک دستهکننده خطی بود. در سال ۱۹۹۲، برنهارد بوزر، ایزابل گیون و وپنیک راهی را برای ایجاد دستهبند غیرخطی، با استفاده قرار دادن هسته برای پیدا کردن ابرصفحه با بیشترین حاشیه، پیشنهاد دادند.[۷] الگوریتم پیشنهادی ظاهراً مشابه است، به جز آنکه تمام ضربهای نقطهای با یک تابع هسته غیرخطی جایگزین شداند. این خصوصیت اجازه میدهد، الگوریتم، برای ابرصفحه با بیشترین حاشیه در یک فضای ویژگی تغییرشکل داده، مناسب باشد. ممکن است، تغییرشکل غیرخطی باشد و فضای تغییر یافته، دارای ابعاد بالاتری باشد. به هر حال دستهبندیکننده، یک ابرصفحه در فضای ویژگی با ابعاد بالا است، که ممکن است در فضای ورودی نیز غیرخطی باشد.
اگر از هسته با تابع گوسین استفاده شود، فضای ویژگی متناظر، یک فضای هیلبرت نامتناهی است. دستهکنندهٔ بیشترین حاشیه، خوش ترتیب است، بنابراین ابعاد نامتناهی، نتیجه را خراب نمیکند. هستههای متداول به صورت زیر هستند:
- چندجملهای (همگن):
- چندجملهای (ناهمگن):
- گوسین تابع پایه شعاعی: ، for گاهی اوقات با استفاده از پارامتر
- تانژانت هذلولی: ، برای برخی (not every) و
هسته با انتقال با تساوی در ارتباط است. همچنین مقدار wدر فضای انتقال یافته برابر است. ضرب نقطهای با w میتواند توسط هسته محاسبه شود یعنی . به هر حال در حالت عادی w' وجود ندارد، بهطوریکه
طبقهبند بردار پشتیبان چندکلاسه (Multi-Class SVC)[ویرایش]
ماشین بردار پشتیبان اساساً یک جداکننده (کلاس بند برای ۲ کلاس) است. در بخش قبلی پایههای تئوری ماشینهای بردار پشتیبان برای دستهبندی دو کلاس تشریح شد. یک تشخیص الگوی چند کلاسی میتواند به وسیلهٔ ترکیب ماشینهای بردار پشیبان دو کلاسی حاصل شود. بهطور معمول دو دید برای این هدف وجود دارد. یکی از آنها استراتژی «یک در مقابل همه» برای دستهبندی هر جفت کلاس و کلاسهای باقیمانده است. دیگر استراتژی «یک در مقابل یک» برای دستهبندی هر جفت است. در شرایطی که دستهبندی اول به دستهبندی مبهم منجر میشود. برای مسائل چند کلاسی٬رهیافت کلی کاهش مسئلهٔ چند کلاسی به چندین مسئله دودویی است. هریک از مسائل با یک جداکننده دودویی حل میشود. سپس خروجی جداکنندههای دودویی SVM با هم ترکیب شده و به این ترتیب مسئله چند کلاس حل میشود.
روش «یک در مقابل همه»[ویرایش]
در این روش، ما نیازمند ابرصفحهای هستیم که دادههای یک کلاس را از دادههای سایر کلاسها بهطور همزمان جداسازی نماید؛ در واقع با این روش تمام نمونهها در بهدست آوردن ابرصفحه بهینه در نظر گرفته خواهند شد؛ به طوریکه دادهها به ازای هر طبقهبند به دو دسته تقسیم میشوند: یک گروه به ازای دادههای کلاس مورد نظر و گروه دیگر شامل تمام نقاط سایر کلاسها. بدین ترتیب برای یک مسئله طبقهبندی با K دسته، نیازمند K طبقهبند ۲ کلاسه هستیم. در زمان آموزش مدل همه K طبقهبند را روی مجموعه آموزش، آموزش میدهیم و سپس در زمان تست مدل هم بررسی میکنیم که هر طبقهبند داده ورودی را در طبقه خود میداند یا خیر. در شرایطی امکان دارد که چند طبقهبند همزمان داده را در کلاس خود اعلام کنند که در اینصورت میتوان از معیارهایی استفاده کرد، یکی از این معیارها انتخاب طبقهبندی است که دورترین ابرصفحه را از داده مورد نظر دارد.
روش «یک در مقابل یک»[ویرایش]
در این روش برخلاف روش قبلی به دنبال پیدا کردن طبقهبند میان هر دو کلاس هستیم پس در نتیجه به طبقهبند نیاز داریم که K در این رابطه تعداد کلاسها است.[۹]
جستارهای وابسته[ویرایش]
منابع[ویرایش]
- ↑ Supervised learning
- ↑ Classification
- ↑ Regression
- ↑ High dimensional space
- ↑ Lagrange Duality Theorems
- ↑ A Tutorial on Support Vector Machines
- ↑ ۷٫۰ ۷٫۱ B. E. Boser, I. M. Guyon, and V. N. Vapnik. A training algorithm for optimal margin classifiers. In D. Haussler, editor, 5th Annual ACM Workshop on COLT, pages 144–152, Pittsburgh, PA, 1992. ACM Press
- ↑ Cortes، Corinna؛ Vapnik، Vladimir (۱۹۹۵). «Support-vector networks» (PDF).
- ↑ روش یک در مقابل یک. «نظارت». دریافتشده در ۲۰۲۴-۰۳-۲۵.
- Christopher J. C. Burges. "A Tutorial on Support Vector Machines for Pattern Recognition". Data Mining and Knowledge Discovery 2:121 - 167, 1998 (http://research.microsoft.com/~cburges/papers/SVMTutorial.pdf)
- "Cortes, Corinna; Vapnik, Vladimir (1995). "Support-vector networks
- http://image.diku.dk/imagecanon/material/cortes_vapnik95.pdf)
- Sergios Theodoridis and Konstantinos Koutroumbas "Pattern Recognition", 4th Edition, Academic Press, 2009, ISBN 978-1-59749-272-0
- Nello Cristianini and John Shawe-Taylor. An Introduction to Support Vector Machines and other kernel-based learning methods.
انتشارات دانشگاه کمبریج , 2000. ISBN 0-521-78019-5 ([۱] SVM Book)
- Huang T. -M. , Kecman V. , Kopriva I. (2006), Kernel Based Algorithms for Mining Huge Data Sets, Supervised, Semi-supervised, and Unsupervised Learning, Springer-Verlag, Berlin, Heidelberg, 260 pp. 96 illus. , Hardcover, ISBN 3-540-31681-7 [۲]
- Vojislav Kecman: "Learning and Soft Computing — Support Vector Machines, Neural Networks, Fuzzy Logic Systems", The MIT Press, Cambridge, MA, 2001.[۳]
- Bernhard Schölkopf and A. J. Smola: Learning with Kernels. MIT Press, Cambridge, MA, 2002. (Partly available on line: [۴].) ISBN 0-262-19475-9
- Bernhard Schölkopf, Christopher J.C. Burges, and Alexander J. Smola (editors). "Advances in Kernel Methods: Support Vector Learning". MIT Press, Cambridge, MA, 1999. ISBN 0-262-19416-3. [۵]
- John Shawe-Taylor and Nello Cristianini. Kernel Methods for Pattern Analysis. Cambridge University Press, 2004. ISBN 0-521-81397-2 ([۶] Kernel Methods Book)
- Ingo Steinwart and Andreas Christmann. Support Vector Machines. Springer-Verlag, New York, 2008. ISBN 978-0-387-77241-7 ([۷] SVM Book)
- P.J. Tan and D.L. Dowe (2004), MML Inference of Oblique Decision Trees, Lecture Notes in Artificial Intelligence (LNAI) 3339, Springer-Verlag, pp1082-1088. (This paper uses حداقل طول پیام (MML) and actually incorporates probabilistic support vector machines in the leaves of درخت تصمیم .)
- Vladimir Vapnik. The Nature of Statistical Learning Theory. Springer-Verlag, 1995. ISBN 0-387-98780-0
- Vladimir Vapnik, S.Kotz "Estimation of Dependences Based on Empirical Data" Springer, 2006. ISBN 0-387-30865-2, 510 pages [this is a reprint of Vapnik's early book describing philosophy behind SVM approach. The 2006 Appendix describes recent development].
- Dmitriy Fradkin and Ilya Muchnik "Support Vector Machines for Classification" in J. Abello and G. Carmode (Eds) "Discrete Methods in Epidemiology", DIMACS Series in Discrete Mathematics and Theoretical Computer Science, volume 70, pp. 13–20, 2006. [۸]. Succinctly describes theoretical ideas behind SVM.
- Kristin P. Bennett and Colin Campbell, "Support Vector Machines: Hype or Hallelujah?", SIGKDD Explorations, 2,2، 2000, 1–13. [۹]. Excellent introduction to SVMs with helpful figures.
- Ovidiu Ivanciuc, "Applications of Support Vector Machines in Chemistry", In: Reviews in Computational Chemistry, Volume 23, 2007, pp. 291–400. Reprint available: [۱۰]
- Catanzaro, Sundaram, Keutzer, "Fast Support Vector Machine Training and Classification on Graphics Processors", In: International Conference on Machine Learning, 2008 [۱۱]
- Colin Campbell and Yiming Ying, Learning with Support Vector Machines, 2011, Morgan and Claypool. ISBN 978-1-60845-616-1. [۱۲]


























![{\displaystyle \min _{\mathbf {w} ,b,{\boldsymbol {\alpha }}}\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b140ef307512ccbafd34429bf40ee6523eac03a)


![{\displaystyle \min _{\mathbf {w} ,b}\max _{\boldsymbol {\alpha }}\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c411ce7bd4a910dba7b0a5a0ee3191146665dec1)

























