زنون الئایی
| زنون الئایی | |
|---|---|
 | |
| زادهٔ | اِلِئا، یونان |
| درگذشت | اِلِئا، یونان |
| دوره | فلسفه دوران باستان |
| حیطه | فلسفهٔ غرب |
| مکتب | مکتب اِلِئایی |
زنون اِلِئایی (به یونانی: Ζήνων ὁ Ἐλεάτης) (به انگلیسی: Zeno of Elea)[۱] (حدود ۴۹۰–۴۹۵ پ. م) در الئا جنوب ایتالیای کنونی (حدود ۴۳۰ پ. م) فیلسوف و ریاضیدان یونان باستان که ارسطو وی را بنیانگذار دیالکتیک نامیدهاست. او شاگرد و دوست پارمنیدس و پیرو و مدافع سرسخت مکتب الئایی بود. مکتبی که بر ثبات و یکتایی واقعیت و بیپایه بودن دانش حسی در مورد کثرت و تغییرپذیری تأکید داشت. زنون بیشتر به خاطر پارادوکسهایی مشهور است که در دفاع از مکتب الئایی و عقیدههای استادش پارمنیدس مطرح کردهاست.
زندگی و آراء[ویرایش]
زنون به گفتهٔ افلاطون به همراه پارمنیدس در حدود سال ۴۴۹ پ. م به آتن سفر کرده و در آنجا دیدار و مباحثاتی با سقراط داشتهاند. وی قبل از سفر به یونان کتابی نوشته بود که بر جای نماندهاست، اما به گفتهٔ افلاطون در آن بهطور غیرمستقیم واقعیتِ حرکت و کثرت را رد کرده بود. در این کتاب چهل پارادوکس (متناقضنما) مطرح شده بود که برخی از آنها تأثیر عمیقی در گسترش ریاضیات داشتهاند. این پارادوکسها به دو دسته قابل تقسیمند، دسته اول دربارهٔ رد تعدد و کثرت و اثبات نوعی وحدت وجود بوده و دستهٔ دوم به مبحث حرکت میپردازد و آن را غیرممکن میداند. در این معماها وی ابتدا یک نظریه از مخالفان پارمنیدس را مطرح کرده و سپس پیامدهای غیرقبول ناشی از پذیرفتن این نظریه را نشان داده و به این ترتیب پوچ بودن آن را ثابت کردهاست. این روش جدلی به نظر میرسد نخستین بار توسط زنون استفاده شده باشد. ارسطو در کتاب فیزیک در پی پاسخ به ادعای زنون در مورد واقعیت نداشتن حرکت برآمده و نشان داد که بحثهای زنون بر پایهٔ تصوراتی اشتباه از مفهوم حرکت و فضا است. با این حال استدلالهای زنون در دوران خود که هنوز منطق به صورت یک علم درنیامده بود بسیار منطقی به نظر میرسیده و میتوانسته طرفداران زیادی را به خود جذب کرده باشد و به عنوان چالشهایی غیرقابل پاسخ برای افرادی که بر واقعیت داشتن حواس تأکید داشتند، راه را برای ترویج شکگرایی سوفسطائیان باز کند.
بر اساس منابع قدیمی زنون همچون پارمنیدس به فعالیت سیاسی در شهر خود میپرداخت و به دلیل توطئه علیه یک حاکم مستبد به مرگ محکوم شد.[۲] داستانهایی در مورد بردباری او در زیر شکنجه و مرگ دردناکی که بر او تحمیل شد، نقل شدهاست. او نیز همچون پارمنیدس بر غیرممکن بودن حرکت استدلال میکرد و چنین میگفت:
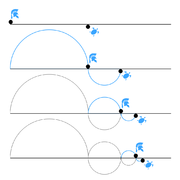
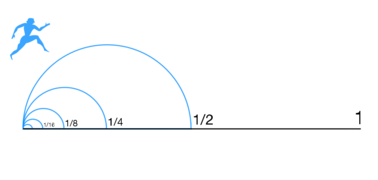
اگر حرکت واقعیت داشته باشد، انتقال است از یک نقطه به نقطهٔ دیگر. پس هرگاه میان این دو نقطه یک خط بکشیم، خواهیم توانست آن را به دو نیم کنیم، و آن نیمه را نیز به دو نیم و همین کار را بر نیمههای دیگر؛ و آنچنان اینکار ادامه خواهد یافت که پایانی نداشته باشد. پس میان این دو نقطه از اجزای بیشمار تشکیل شدهاست، که یک جسم هنگام حرکت باید از بیشمار قسمت عبور کند، که اینکار به زمان بینهایت احتیاج دارد؛ و بنابر این حرکت هیچگاه انجام نخواهد شد.
پارادوکسهای زنون[ویرایش]
پارادوکسهای زنون بیش از دو هزار سال است که فیلسوفان، ریاضیدانان، و فیزیکدانان را، به چالش کشیده و آنها را تحت تأثیر قرار دادهاست. معروفترین آنها، استدلال در برابر حرکت است که ارسطو در کتاب فیزیک خود شرح دادهاست.[۳]
-
آشیل و لاک پشت
-
تناقض دو بخشی
-
پیکان
-
ردیفهای متحرک
جستارهای وابسته[ویرایش]
منابع[ویرایش]
- ↑ کاپلستون، کاپلستون، جلد اول، ترجمهٔ جلالالدین مجتبوی
- ↑ زندگی و آراء فیلسوفان برجسته، نوشتهٔ دیوژن لائرتی
- ↑ فیزیک نوشته ارسطو
پیوند به بیرون[ویرایش]
- اهالی یونان سده ۵ (پیش از میلاد)
- درگذشتگان دهه ۴۳۰ (پیش از میلاد)
- افراد الجیبیتی اهل ایتالیا
- الجیبیتی باستان
- زادگان دهه ۴۹۰ (پیش از میلاد)
- زادگان دهه ۴۹۰ (میلادی)
- فیثاغورسیان
- فیلسوفان الئایی
- فیلسوفان پیشاسقراطی
- فیلسوفان سده ۵ (پیش از میلاد)
- فیلسوفان مگنا گراسیا
- فیلسوفان یونان باستان
- متافیزیکپژوهان
- منتقدان فرهنگی
- دیالکتیک
- شناختشناسان
- تاریخ منطق
- تاریخ ریاضیات
- تاریخ فلسفه
- تاریخ علم
- تاریخ ایدهها
- منطقدانان
- فرافیلسوفان
- هستیشناسان
- پارادوکسها
- فیلسوفان منطق
- فیلسوفان ریاضیات
- فیلسوفان علم
- منتقدان اجتماعی
- فیلسوفان اجتماعی