برگ‌سازی

مقطع ۲-بعدی از برگ‌سازی ریب

مدل ۳-بعدی از برگ‌سازی ریب

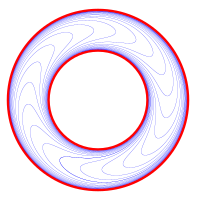
در شاخه هندسه دیفرانسیل از ریاضیات، برگ‌سازی (به انگلیسی: Foliation)، نوعی رابطه هم‌ارزی روی یک n-منیفلد است. در رابطه هم‌ارزی مذکور، هر رده هم‌ارزی برابر زیرمنیفلدهای همبندی است که به‌طور یک-به-یک ایمرس شده و همگی دارای بعدی برابر با p می‌باشند. منیفلدهای مذکور روی تجزیه فضای مختصات حقیقی $\mathbb {R} ^{n}$ به هم‌دسته‌های $x+\mathbb {R} ^{p}$ که در $\mathbb {R} ^{p}$ به صورت استاندارد نشانده شده‌اند، مدل‌سازی می‌شوند. این رده‌های هم‌ارزی را برگ‌های این برگ‌سازی می‌گویند. اگر منیفلد مورد نظر و/یا زیرمنیفلدهای آن ملزم به داشتن خواصی چون قطعه-به-قطعه خطی بودن، دیفرانسیل‌پذیری (از رده $C^{r}$) یا ساختاری تحلیلی شوند، آنگاه می‌توان به ترتیب برگ‌سازی‌های قطعه-به-قطعه خطی، دیفرانسیل‌پذیر یا تحلیلی ایجاد نمود. در مهم‌ترین حالت، برگ‌سازی از رده $C^{r}$ را به صورت $r\geq 1$ در نظر می‌گیرند (چرا که حالت $C^{0}$، برگ‌سازی توپولوژیکی است). عدد p (بعد برگ‌ها) را بعد برگ‌سازی نامیده و $q=n-p$ را هم‌بعد آن گویند.

در برخی مقالاتی که ریاضی-فیزیک‌دانان در مورد نسبیت عام نگاشته‌اند، اصطلاح برگ‌سازی (یا قاچ زدن، slicing) را جهت توصیف شرایطی به کار می‌برند که منیفلد لورنتزی مد نظر (فضا-زمان (p+1)-بعدی)، به ابر رویه‌های p بعدی تجزیه شده باشد، به گونه‌ای که می‌توان آن را به صورت مجوعه‌های سطحی (level sets) از یک تابع هموار حقیقی-مقداری (میدان نرده‌ای) در نظر گرفت که گرادیانش همه جا ناصفر است؛ همچنین اغلب این تابع هموار را تابع زمانی در نظر می‌گیرند، یعنی گرادیان آن زمان-گونه است، چنان‌که مجموعه‌های سطحی‌اش همگی ابررویه‌هایی فضا-گونه اند. در تمایز با واژه‌شناسی استاندارد ریاضیاتی، این ابررویه‌ها را اغلب برگ‌های (یا قاچ‌های) برگ‌سازی گویند. توجه کنید که با وجود این که این شرایط از نظر ریاضیاتی موجب ایجاد برگ‌سازی با هم-بعد ۱ می‌شود، اما مثال‌های این نوع برگ‌سازی در عمل از نظر سرتاسری بدیهی اند؛ در حالی که برگ‌های برگ‌سازیی با هم-بعد ۱ همیشه به‌طور موضعی، مجموعه‌های سطحی از یک تابع اند، این برگ‌سازی‌ها را عموماً نمی‌توان در حالت سرتاسری به این صورت بیان نمود، چرا که ممکن است یک برگ از چارت (یا کارت) بدیهی‌ساز موضعی بی‌نهایت بار عبور کند و همچنین ممکن است هولونومی حول یک برگ، وجود توابعی که به‌طور سرتاسری برای برگ‌ها سازگار اند را نیز مانع شود. به عنوان مثال، درحالی که ۳-کره دارای برگ‌سازی معروفی با هم-بعد ۱ است که توسط Reeb کشف شد، برگ‌سازی با هم-بعد ۱ از منیفلد بسته دلخواه را نمی‌توان مجهز به مجموعه‌های سطحی یک تابع هموار نمود، چرا که تابع هموار دلخواه روی یک منیفلد بسته لزوماً دارای نقاط بحرانی در ماکسیمم‌ها و مینیمم‌هایش می‌باشد.

منابع

• Anosov, D.V. (2001) [1994], "Foliation", Encyclopedia of Mathematics, EMS Press
• Candel, Alberto; Conlon, Lawrence (2000). Foliations I. Graduate Studies in Mathematics. Vol. 23. Providence, Rhode Island: American Mathematical Society. ISBN 0-8218-0809-5.
• Candel, Alberto; Conlon, Lawrence (2003). Foliations II. Graduate Studies in Mathematics. Vol. 60. Providence, Rhode Island: American Mathematical Society. ISBN 0-8218-0809-5.
• Gourgoulhon, Éric (2012). 3+1 Formalism in General Relativity. Lecture Notes in Physics. Vol. 846. Heidelberg, New York, Dordrecht, London: Springer. doi:10.1007/978-3-642-24525-1. ISBN 978-3-642-24524-4.
• Haefliger, André (1970), "Feuilletages sur les variétés ouvertes", Topology, 9 (2): 183–194, doi:10.1016/0040-9383(70)90040-6, ISSN 0040-9383, MR 0263104
• Lawson, H. Blaine (1974), "Foliations", Bulletin of the American Mathematical Society, 80 (3): 369–418, doi:10.1090/S0002-9904-1974-13432-4, ISSN 0002-9904, MR 0343289
• Moerdijk, Ieke; Mrčun, J. (2003), Introduction to foliations and Lie groupoids, Cambridge Studies in Advanced Mathematics, vol. 91, Cambridge University Press, ISBN 978-0-521-83197-0, MR 2012261
• Reeb, Georges (1952), Sur certaines propriétés topologiques des variétés feuilletées, Actualités Sci. Ind. , no. 1183, Hermann & Cie. , Paris, MR 0055692
• Thurston, William (1974), "The theory of foliations of codimension greater than one", Commentarii Mathematici Helvetici, 49: 214–231, doi:10.1007/BF02566730, ISSN 0010-2571, MR 0370619, S2CID 120603728
• Thurston, William P. (1976), "Existence of codimension-one foliations", Annals of Mathematics, Second Series, 104 (2): 249–268, doi:10.2307/1971047, ISSN 0003-486X, JSTOR 1971047, MR 0425985