نابرابری ینسن

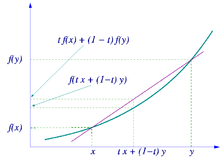
نابرابری ینسن بر روی نمودار

نابرابری ینسن نابرابری اساسی در مبحث توابع محدب و مقعر است. این به دلیل عمومیت این نابرابری، خود مبنای بسیاری از نابرابری‌های مهم است، به خصوص در تجزیه و تحلیل و تئوری اطلاعات. این نابرابری بنام ریاضیدان دانمارکی یوهان لودویگ ینسن (به دانمارکی: Johan Ludvig William Valdemar Jensen)، نامگذاری شده و در ۱۷ در ژانویه ۱۹۰۵ در یک کنفرانس مربوط به ریاضیات در دانمارک معرفی شده‌اند. طبق فرضیه‌های دیگری این نابرابری قبل از آن توسط اتو هولدر، (به آلمانی: Otto Hölder) ریاضیدان آلمانی در سال ۱۸۸۹ استفاده شده.

جملات

بیان

برای یک تابع محدب $f\;$ و برای $\lambda _{i}\;$ غیر منفی: $\sum _{i=1}^{n}\lambda _{i}=1$، بنابراین:

$f\left(\sum _{i=1}^{n}\lambda _{i}x_{i}\right)\leq \sum _{i=1}^{n}\lambda _{i}f\left(x_{i}\right).$

اثبات استنتاجی

برای هر $\lambda$ حقیقی بین ۰ و ۱ :

$f(\lambda x+(1-\lambda )y)\leq \lambda f(x)+(1-\lambda )f(y)$

اثبات ینسن

$f\left({\frac {x+y}{2}}\right)\leq {\frac {f(x)+f(y)}{2}}$

$f\left({\frac {\sum _{i=1}^{n}x_{i}}{n}}\right)\leq {\frac {\sum _{i=1}^{n}f\left(x_{i}\right)}{n}}$

$f\left({\frac {\sum _{i=1}^{n}k_{i}x_{i}}{\sum _{i=1}^{n}k_{i}}}\right)\leq {\frac {\sum _{i=1}^{n}k_{i}f\left(x_{i}\right)}{\sum _{i=1}^{n}k_{i}}}$

$f\left(\sum _{i=1}^{n}\lambda _{i}x_{i}\right)\leq \sum _{i=1}^{n}\lambda _{i}f\left(x_{i}\right)$

کاربردها

از نابرابری ینسن در اثبات نابرابری‌های دیگر استفاده می‌شود. به‌طور مثال در اثبات نابرابری میانگین حسابی-هندسی و نابرابری کی فان (به انگلیسی: Ky Fan inequality) از این نابرابری استفاده می‌شود.

پیوند به بیرون

نابرابری ینسن، مؤسسه‌ای بین‌المللی ولفرم ریسرچ