قضیه چهار رنگ

مثالی از یک نقشه چهاررنگ

نقشه آمریکا، رنگ‌شده با چهار رنگ، بدون در نظر گرفتن آب‌ها و کشورهای دیگر

قَضیّهٔ چهار رَنگ یا حدس چهار رنگ از مسائل مشهور و قدیمی ریاضیات است که سال‌ها اثبات‌نشده مانده بود. به بیان ساده (و نادقیق) این قضیه می‌گوید:

برای رنگ کردن هر نقشه به‌طوری‌که کشورها و نواحی همسایه در نقشه هم‌رنگ نباشند فقط چهار رنگ کافی است.

سه رنگ برای نقشه‌های ساده‌تر کافیست ولی یک رنگ چهارم اضافی برای برخی نقشه‌ها لازم است. مثل نقشه‌هایی که در آن‌ها یک ناحیه با تعداد فرد نواحی دیگر احاطه شده‌است که به یکدیگر در یک دایره وصل هستند. قضیه ۵ رنگ که اثباتی کوتاه و ابتدایی دارد، بیان می‌کند که ۵ رنگ برای رنگ آمیزی نقشه کافیست . این قضیه در اواخر قرن ۱۹ اثبات شده‌است (هیووو ۱۸۹۰). اثبات اینکه ۴ رنگ کافیست بسیار سخت تر است. تعدادی اثبات‌های غلط و مثال‌های نقض از زمان ارائه قضیه ۴ رنگ در ۱۸۵۲ بیان شده‌اند.

این مسئله به صورت معادله ابتدا درسال۱۸۵۲ عنوان شد و سرانجام در سال ۱۹۷۶ با کمک رایانه توسط کی اپپل و و. هیکن حل شد. این اولین قضیه مهمی بود که با استفاده از کامپیوتر به اثبات رسید. آن‌ها نشان دادند که مجموعه‌ای از ۱۹۳۶ نقشه وجود دارد که هیچ‌کدام از آن‌ها نمی‌توانند قسمتی از یکی از کوچکترین مثال نقض‌های قضیه چهار رنگ باشند. اپل و هیکن از یک برنامه کامپیوتری خاص منظوره استفاده کردند تا ثابت کنند هیچ‌کدام از این نقشه‌ها از این قاعده مستثنا نیستند. علاوه بر این هر نقشه‌ای فارغ از این که مثال نقض هست یا نه، حتماً قسمتی را شامل می‌شود که شبیه یکی از آن ۱۹۳۶ نقشه می‌باشد و اثبات این نیاز به صدها صفحه تحلیل دست نویس بود. اپل و هیکن نتیجه گرفتند که اگر بخواهد کوچکترین مثال نقضی وجود داشته باشد باید شامل یکی از آن ۱۹۳۶ نقشه باشد. این تناقض به این معنی بود که هیچ مثال نقضی وجود ندارد و قضیه درست می‌باشد. در ابتدا اثبات آن‌ها از طرف همه ریاضیدان‌ها مورد تأیید واقع نشد، چرا که چک کردن یک اثبات کامپیوتری توسط انسان امکان‌پذیر نبود (Swart ۱۹۸۰).

قاعده‌سازی دقیق قضیه

بیان شهودی قضیه چهار رنگ، یعنی:"در هر افرازی از یک صفحه، که نقشه نامیده می‌شود، هر ناحیه می‌تواند به‌طوری رنگ شود که هیج دو ناحیه مجاوری هم رنگ نباشند و در این رنگ آمیزی از بیشتر از چهار رنگ استفاده نشود"، نیازمند تفسیر و درک مناسب و درستی است. برای مثال هر ناحیه نقشه باید پیوسته باشد. در دنیای واقعی، همه کشورها پیوسته نیستند(برای مثال ایالت آلاسکا در آمریکا و نخجوان در آذربایجان). به علت یکپارچه نبودن قلمرو بعضی کشورها ممکن است چهار رنگ کافی نباشد.

نمونه‌ای از نقشه کشور جمهوری آذربایجان با نواحی غیر پیوسته.

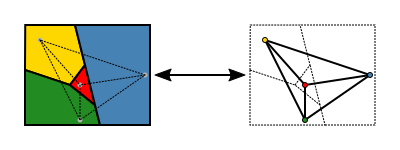
یک بیان ساده‌تر این قضیه به کمک تئوری گراف می‌باشد. می‌توان مجموعه نواحی یک نقشه را به یک گراف بدون جهت نظیر کرد که هر راس یک ناحیه و هر یال دو رأس‌های دو ناحیه که مجاور هستند را به هم متصل می‌کند. گراف حاصل مسطح می‌باشد: یعنی این گراف را می‌توان در صفحه نقشه قرار داد و هر راس را در جای دلخواهی از ناحیه متناظر آن گذاشت، بدون آنکه هیچ دو یالی همدیگر را قطع کنند. به بیان گرافی، قضیه چهار رنگ بیان می‌کند که رئوس یک گراف مسطح را می‌توان با چهار رنگ رنگ آمیزی کرد به‌طوری‌که هیچ دو راس مجاور همرنگ نباشند.((Thomas ۱۹۹۸، ص. ۸۴۹); (Wilson ۲۰۰۲))

تاریخچه

تلاش‌های اولیه برای اثبات

conjecture اولین بار در سال ۱۸۵۲ مطرح شد. در آن هنگام فرانسیس گاتری مشغول رنگ آمیزی نقشه انگلستان بود که متوجه شد چهار رنگ برای این کار کافیست. فرانسیس این موضوع را با برادرش فردریک مطرح کرد، که بعداً وی آن را به پیش د مرگان برد. اولین منبع منتشر شده از آرتور کیلی می‌باشد(آرتور کیلی ۱۸۷۹).

تلاش‌های ناموفق بسیاری برای اثبات این قضیه انجام شده‌است. اثبات آلفرد کمپه در سال ۱۸۷۹ که بسیار مورد قبول واقع شد و اثبات دیگری که پیتر گاتری تیت در ۱۸۸۰ مطرح کرد، همگی از این دست بودند. هر دوی این اثبات‌های اشتباه ۱۱ سال بعد از مطرح شدنشان به ترتیب توسط پرسی هیوود و ژولیوس پترسن نقض شدند.

اثبات توسط کامپیوتر

در دهه‌های ۶۰ و ۷۰ میلادی هاینریش هیش، ریاضیدان آلمانی، روش‌های اثبات به کمک کامپیوتر را توسعه داد. متأسفانه در این زمان به وی فرصت استفاده از ابررایانه داده نشد تا کارش را ادامه دهد. ولی دیگران روش‌های او را ادامه دادند. در سال ۱۹۷۶، در حالی که گروه‌هایی از ریاضیدانان در رقابت برای بدست آوردن اثبات کامل بودند، کنس اپل و وولفانگ هیکن در دانشگاه Illinois اعلام کردند که قضیه را اثبات کرده‌اند. آن‌ها در یک سری کارهای الگوریتمی توسط John A. Koch همیاری شده بودند (Wilson ۲۰۰۲).

اگر حدس چهار رنگ نادرست بود، حداقل یک نقشه وجود داشت با کمترین تعداد نواحی ممکن، که به پنج رنگ نیاز داشت. اثبات نشان داد که چنین کوچکترین مثال نقضی نمی‌تواند وجود داشته باشد؛ از طریق دو مفهوم فنی((Wilson ۲۰۰۲); (Appel و Haken ۱۹۸۹); (Thomas ۱۹۹۸، صص. ۸۵۲–۸۵۳)):

• مجموعی اجتناب ناپذیر دربر دارندهٔ نواحی ای می‌باشد که هر نقشه حداقل باید یکی از آن‌ها را دارا باشد.
• یک آرایش کاهش پذیر وضعیتی از کشورهاست که نمی‌توانند در یک مثال نقض کمینه اتفاق بیفتند. اگر در یک نقشه یک آرایش کاهش پذیر وجود داشته باشد، نقشه می‌تواند به یک نقشه کوچکتر کاهش یابد. حال اگر این نقشه کوچکتر بتواند با چهار رنگ رنگ آمیزی شود، نقشه اصلی هم می‌تواند با چهار رنگ رنگ آمیزی شود. این به این معنی است که اگر نقشه اصلی نتواند با چهار رنگ رنگ شود نقشه کوچکتر هم نمی‌تواند، پس نقشه اصلی کمینه نیست.

با استفاده از قوانین و روش‌های ریاضی بر پایهٔ خواص آرایش‌های کاهش پذیر، اپل و هیکن یک مجموعه اجتناب ناپذیر از آرایش‌های کاهش پذیر یافتند که نشان می‌دهد هیچ مثال نقض کمینه‌ای وجود ندارد. اثبات آن‌ها تعداد بینهایت نقشه ممکن را به ۱۹۳۶ آرایش کاهش پذیر(که بعداً به ۱۴۷۶ رسید) کاهش داد. پروسه چک کردن این تعداد حالت با کامپیوتر بیشتر از هزار ساعت به طول انجامید(Appel & Haken ۱۹۸۹).

ساده‌سازی و بازبینی

الگوریتم‌هایی که برای اثبات قضیه استفاده شدند داری پیچیدگی زمانی (O(n^۲ می‌باشد که n تعداد رأس‌ها است. در سال ۲۰۰۵ Benjamin Werner و George Gonthier به کمک ‍‍‍‍‍Coq‍‍ برای اثبات قضیه قاعدی‌سازی کردند. این کار نیاز به اعتماد به برنامه‌های کامپیوتری که برای درستی سنجی حالت‌های خاص بودند را از بین برد. حال تنها نیاز است به Coq kernel اعتماد شود(Gonthier ۲۰۰۸).

خلاصه ایده اثبات

این قسمت خلاصه‌ای است بر مبنای مقدمه کتاب Every Planar Map is Four Colorable نوشتهٔ اپل و هیکن. با وجود اینکه اثبات اولیه کمپه اشتباه بود، ابزار پایه‌ای برای اثبات قضیه را ساخت. اظهارات کمپه بدین صورت بود: اگر نواحی مسطحی که با گراف جدا شده‌اند مثلث نباشند، به عبارت دیگر دقیقاً سه گوشه در مرزهایشان نداشته باشند، می‌توانیم به آن‌ها بدون معرفی رئوس، یال اضافه کنیم تا مثلثی شوند. اگر این گراف مثلثی قابل رنگ شدن با ۴ رنگ یا کمتر باشد گراف اصلی هم قابل رنگ شدن است چرا که همان نحوهٔ رنگ شدن در صورت از بین بردن یال‌ها مجاز است.

منابع

• Allaire, F. (1997), "Another proof of the four colour theorem—Part I", Proceedings, 7th Manitoba Conference on Numerical Mathematics and Computing, Congr. Numer., vol. 20, pp. 3–72
• Appel, Kenneth; Haken, Wolfgang (1977), "Every Planar Map is Four Colorable Part I. Discharging", Illinois Journal of Mathematics, vol. 21, pp. 429–490
• Appel, Kenneth; Haken, Wolfgang; Koch, John (1977), "Every Planar Map is Four Colorable Part II. Reducibility", Illinois Journal of Mathematics, vol. 21, pp. 491–567
• Appel, Kenneth; Haken, Wolfgang (1977), "Solution of the Four Color Map Problem", Scientific American, vol. 237, no. 4, pp. 108–121, doi:10٫1038/scientificamerican1077-108 {{citation}}: Check |doi= value (help); Unknown parameter |month= ignored (help)
• Appel, Kenneth; Haken, Wolfgang (1989), Every Planar Map is Four-Colorable, Providence, RI: American Mathematical Society, ISBN 0-8218-5103-9
• Bernhart, Frank R. (1977), "A digest of the four color theorem.", Journal of Graph Theory, vol. 1, pp. 207–225, doi:10٫1002/jgt.3190010305 {{citation}}: Check |doi= value (help); Cite has empty unknown parameter: |1= (help)
• Cayley, Arthur (1879), "On the colourings of maps", Proc. Royal Geographical Society, Blackwell Publishing, vol. 1, no. 4, pp. 259–261, doi:10٫2307/1799998, JSTOR 1799998 {{citation}}: Check |doi= value (help)
• Fritsch, Rudolf; Fritsch, Gerda (1998), The Four Color Theorem: History, Topological Foundations and Idea of Proof, New York: Springer, ISBN 978-0-387-98497-1
• Gonthier, Georges (2008), "Formal Proof—The Four-Color Theorem" (PDF), Notices of the American Mathematical Society, vol. 55, no. 11, pp. 1382–1393
• Gonthier, Georges (2005), A computer-checked proof of the four colour theorem (PDF), unpublished
• Hadwiger, Hugo (1943), "Über eine Klassifikation der Streckenkomplexe", Vierteljschr. Naturforsch. Ges. Zürich, 88: 133–143
• Heawood, P. J. (1890), "Map-Colour Theorem", Quarterly Journal of Mathematics, Oxford, vol. 24, pp. 332–338
• Magnant, C.; Martin, D. M. (2011), "Coloring rectangular blocks in 3-space", Discussiones Mathematicae Graph Theory, 31 (1): 161–170, archived from the original on 4 February 2022, retrieved 9 December 2011
• Nash-Williams, C. St. J. A. (1967), "Infinite graphs—a survey", J. Combinatorial Theory, 3: 286–301, MR 0214501.
• O'Connor; Robertson (1996), The Four Colour Theorem, MacTutor archive, archived from the original on 16 January 2013, retrieved 9 December 2011
• Pegg, A.; Melendez, J.; Berenguer, R.; Sendra, J. R.; Hernandez; Del Pino, J. (2002), "Book Review: The Colossal Book of Mathematics" (PDF), Notices of the American Mathematical Society, 49 (9): 1084–1086, Bibcode:2002ITED...49.1084A, doi:10.1109/TED.2002.1003756
• Reed, Bruce; Allwright, David (2008), "Painting the office", Mathematics-in-Industry Case Studies, 1: 1–8, archived from the original on 3 February 2013, retrieved 9 December 2011
• Ringel, G.; Youngs, J.W.T. (1968), "Solution of the Heawood Map-Coloring Problem", Proc. Nat. Acad. Sci. USA, vol. 60, no. 2, pp. 438–445, doi:10٫1073/pnas.60٫2.438, PMC 225066, PMID 16591648 {{citation}}: Check |doi= value (help)
• Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1996), "Efficiently four-coloring planar graphs", Efficiently four-coloring planar graphs, STOC'96: Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, ACM Press, pp. 571–575, doi:10٫1145/237814٫238005 {{citation}}: Check |doi= value (help)
• Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1997), "The Four-Colour Theorem", J. Combin. Theory Ser. B, vol. 70, no. 1, pp. 2–44, doi:10٫1006/jctb.1997٫1750 {{citation}}: Check |doi= value (help)
• Saaty, Thomas; Kainen, Paul (1986), "The Four Color Problem: Assaults and Conquest", Science, New York: Dover Publications, 202 (4366): 424, Bibcode:1978Sci...202..424S, doi:10٫1126/science.202٫4366٫424, ISBN 0-486-65092-8 {{citation}}: Check |doi= value (help)
• Swart, ER (1980), "The philosophical implications of the four-color problem" (PDF), American Mathematical Monthly, Mathematical Association of America, vol. 87, no. 9, pp. 697–702, doi:10٫2307/2321855, JSTOR 2321855, archived from the original (PDF) on 14 July 2010, retrieved 9 December 2011 {{citation}}: Check |doi= value (help)
• Thomas, Robin (1998), "An Update on the Four-Color Theorem" (PDF), Notices of the American Mathematical Society, vol. 45, no. 7, pp. 848–859
• Thomas, Robin (1995), The Four Color Theorem
• Thomas, Robin, Recent Excluded Minor Theorems for Graphs (PDF), p. 14, archived from the original (PDF) on 3 August 2016, retrieved 9 December 2011
• Wilson, Robin (2002), Four Colors Suffice, London: Penguin Books, ISBN 0-691-11533-8